Почему существуют пределы того, что могут прогнозировать физики?
Если делить вещество во Вселенной на все меньшие и меньшие составляющие, вы в конечном итоге достигнете ограничения, столкнувшись с фундаментальной и неделимой частицей. Все макроскопические объекты можно поделить на молекулы, даже атомы, затем электроны (которые фундаментальны) и ядра, затем на протоны и нейтроны, и, наконец, внутри них будут кварки и глюоны. Электроны, кварки и глюоны — примеры фундаментальных частиц, которые нельзя разделить еще больше. Но как такое возможно, чтобы у самого времени и пространства были такие же ограничения? Почему вообще существуют значения Планка, которые уже нельзя делить дальше?
Чтобы понять, откуда берется планковская величина, стоит начать с двух столпов, которые управляют реальностью: общая теория относительности и квантовая физика.
Общая теория относительности связывает материю и энергию, существующие во Вселенной, с кривизной и деформацией ткани пространства-времени. Квантовая физика описывает, как различные частицы и поля взаимодействуют между собой внутри ткани пространства-времени, в том числе и в очень малых масштабах. Существует две фундаментальные физические константы, которые играют роль в общей теории относительности: G — гравитационная постоянная Вселенной, и c — скорость света. G возникает, поскольку задает показатель деформации пространства-времени в присутствии вещества и энергии; c — потому что это гравитационное взаимодействие распространяется в пространстве-времени на скорости света.
Квантовая физика описывает, как различные частицы и поля взаимодействуют между собой внутри ткани пространства-времени, в том числе и в очень малых масштабах. Существует две фундаментальные физические константы, которые играют роль в общей теории относительности: G — гравитационная постоянная Вселенной, и c — скорость света. G возникает, поскольку задает показатель деформации пространства-времени в присутствии вещества и энергии; c — потому что это гравитационное взаимодействие распространяется в пространстве-времени на скорости света.
В квантовой механике тоже появляется две фундаментальные константы: c и h, где последняя — это постоянная Планка. c — это ограничение скорости всех частиц, скорость, с которой должны двигаться все безмассовые частицы, и максимальная скорость, с которой может распространяться любое взаимодействие. Постоянная Планка была невероятной важной для описания того, как квантуются (считаются) квантовые энергетические уровни, взаимодействия между частицами и все возможные исходы событий. Электрон, вращающийся вокруг протона, может иметь любое количество энергетических уровней, но все они появляются дискретными шагами, и размер этих шагов определяется h.
Электрон, вращающийся вокруг протона, может иметь любое количество энергетических уровней, но все они появляются дискретными шагами, и размер этих шагов определяется h.
Совместите три этих постоянных: G, c и h, и сможете использовать разные их сочетания для построения шкалы длины, массы и периода времени. Они известны, соответственно, как длина Планка, масса Планка и время Планка. (Можно построить и другие величины, например, энергию Планка, температуру Планка и так далее). Все это, в общем и целом, шкала длины, массы и времени, при которых — в отсутствие какой-либо другой информации — будут значительными квантовые эффекты. Есть хорошие причины полагать, что это так и есть, и довольно легко понять — почему так.
Представьте, что у вас есть частица определенной массы. Вы задаете вопрос: «Если бы моя частица имела такую массу, в насколько малый объем ее нужно сжать, чтобы она стала черной дырой?». Вы еще можете спросить: «Если бы у меня была черная дыра определенного размера, за какое время частица, двигающаяся на скорости света, преодолела бы расстояние, равное этому размеру?». Масса Планка, длина Планка и время Планка соответствуют именно таким величинам: черная дыра планковской массы будет планковской длины и пересекаться со скорость света за планковское время.
Масса Планка, длина Планка и время Планка соответствуют именно таким величинам: черная дыра планковской массы будет планковской длины и пересекаться со скорость света за планковское время.
Но планковская масса намного, намного более массивна, чем любые частицы, которые мы когда-либо создавали; она в 1019 раз тяжелее протона! Длина Планка, точно так же, в 1014 раз меньше любого расстояния, которое мы когда-либо зондировали, а планковское время в 1025 раз меньше любого прямо измеренного. Эти масштабы никогда не были напрямую доступны для нас, но они важны по другой причине: планковская энергия (которую вы можете получить, поместив планковскую массу в E = mc2) – это масштаб, при котором квантово-гравитационные эффекты начинают приобретать важность и значимость.
Это значит, что при энергии такой величины — или временных масштабах короче времени Планка, или шкалы длины меньше длины Планка — наши нынешние законы физики должны нарушаться.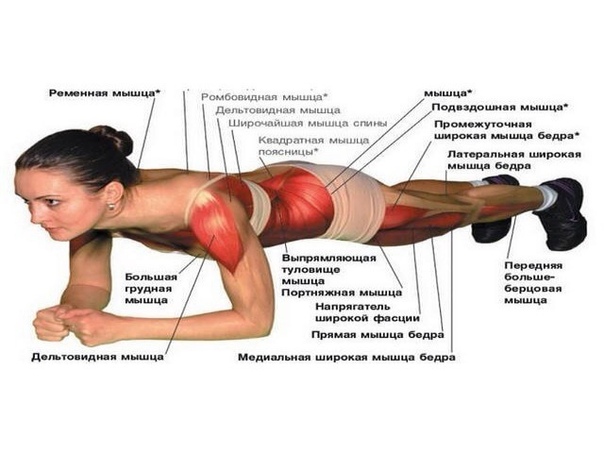 В игру вступают эффекты квантовой гравитации, и предсказания общей теории относительности перестают быть надежными. Кривизна пространства становится очень большой, а значит и «фон», который мы используем для расчета квантовых величин, тоже перестает быть надежным. Неопределенность энергии и времени означает, что неопределенности становятся выше значений, которые мы знаем как рассчитать. Короче говоря, привычная нам физика больше не работает.
В игру вступают эффекты квантовой гравитации, и предсказания общей теории относительности перестают быть надежными. Кривизна пространства становится очень большой, а значит и «фон», который мы используем для расчета квантовых величин, тоже перестает быть надежным. Неопределенность энергии и времени означает, что неопределенности становятся выше значений, которые мы знаем как рассчитать. Короче говоря, привычная нам физика больше не работает.
Для нашей Вселенной это не проблема. Эти энергетические масштабы в 1015 раз выше, чем те, которых может достичь Большой адронный коллайдер, и в 100 000 000 раз больше самых энергетических частиц, которые создает сама Вселенная (космические лучи высокой энергии), и даже в 10 000 раз выше показателей, которых достигла Вселенная сразу после Большого Взрыва. Но если бы мы хотели исследовать эти пределы, есть одно место, где они могут быть важны: в сингулярностях, расположенных в центрах черных дыр.
В этих местах массы, значительно превосходящие планковскую массу, сжимаются в размер, теоретически меньший длины Планка. Если во Вселенной есть место, где мы сводим все линии в одну и входим в режим Планка, то это оно. Мы не можем получить к нему доступ сегодня, потому что оно закрыто горизонтом событий черной дыры и недоступно. Но если мы будем достаточно терпеливы — а терпения потребуется много — Вселенная даст нам такую возможность.
Если во Вселенной есть место, где мы сводим все линии в одну и входим в режим Планка, то это оно. Мы не можем получить к нему доступ сегодня, потому что оно закрыто горизонтом событий черной дыры и недоступно. Но если мы будем достаточно терпеливы — а терпения потребуется много — Вселенная даст нам такую возможность.
Видите ли, черные дыры со временем медленно распадаются. Интеграция квантовой теории поля в искривленном пространстве-времени ОТО означает, что небольшое количество излучения испускается в пространстве вне горизонта событий, а энергия для этого излучения исходит из массы черной дыры. Со временем масса черной дыры уменьшается, горизонт событий сжимается, и через 1067 лет черная дыра солнечной массы полностью испарится. Если бы мы могли получить доступ ко всему излучению, покинувшему черную дыру, включая самые последние моменты ее существования, мы, несомненно, смогли бы собрать воедино все квантовые эффекты, которых не предсказывали наши лучшие теории.
Совсем не обязательно, что пространство нельзя разделить на еще более мелкие единицы, чем планковская длина, и что время нельзя разделить на единицы меньшие, чем планковское время. Просто мы знаем, что наше описание Вселенной, в том числе наши законы физики, не могут выйти за пределы этих масштабов. Квантуемо ли пространство? Течет ли время непрерывно на самом деле? И что нам делать с тем фактом, что все известные фундаментальные частицы во Вселенной имеют массы намного, намного меньше планковской? На эти вопросы в физике нет ответов. Планковские масштабы не столь фундаментальны в ограничении Вселенной, сколь в нашем понимании Вселенной. Поэтому мы продолжаем экспериментировать. Возможно, когда у нас будет больше знаний, мы получим ответы на все вопросы. Пока нет.
Просто мы знаем, что наше описание Вселенной, в том числе наши законы физики, не могут выйти за пределы этих масштабов. Квантуемо ли пространство? Течет ли время непрерывно на самом деле? И что нам делать с тем фактом, что все известные фундаментальные частицы во Вселенной имеют массы намного, намного меньше планковской? На эти вопросы в физике нет ответов. Планковские масштабы не столь фундаментальны в ограничении Вселенной, сколь в нашем понимании Вселенной. Поэтому мы продолжаем экспериментировать. Возможно, когда у нас будет больше знаний, мы получим ответы на все вопросы. Пока нет.
Планковская длина — Planck length
Наименьшая рассматриваемая длина
В физике , то длина Планка , обозначается ℓ Р , является единицей длины . Это также уменьшенная комптоновская длина волны частицы с массой Планка . Это равно 1,616 255 (18) × 10 −35 м . Это базовая единица в системе единиц Планка , разработанной физиком Максом Планком . {- 35} \ \ mathrm {m}}
{- 35} \ \ mathrm {m}}
Две цифры, заключенные в круглые скобки, представляют собой расчетную стандартную ошибку, связанную с сообщенным числовым значением.
Длина Планки составляет около 10 -20 раз диаметра протона . Его можно определить, используя радиус предполагаемой частицы Планка .
История
В 1899 году Макс Планк предположил, что существуют некоторые фундаментальные естественные единицы для длины, массы, времени и энергии. Он получил их с помощью анализа размерностей , используя только гравитационную постоянную Ньютона, скорость света и «единицу действия», которая позже стала постоянной Планка. Полученные им природные единицы стали известны как «Планковская длина», « Планковская масса », « Планковское время » и « Планковская энергия ».
Визуализация
Размер планковской длины можно визуализировать следующим образом: если бы частица или точка размером около 0,1 мм (диаметр человеческого волоса, который является наименьшим или близким к наименьшему, который может видеть невооруженный глаз), были увеличены в размере до если она велика, как наблюдаемая Вселенная , то внутри этой «точки» размером со Вселенную планковская длина будет примерно равна размеру реальной точки размером 0,1 мм. {- 4}}
{- 4}}
Теоретическая значимость
Планковская длина — это масштаб, на котором, как полагают, квантовые гравитационные эффекты начинают проявляться в так называемой квантовой пене , и где взаимодействия требуют анализа действующей теории квантовой гравитации . Планковская длина также может представлять диаметр наименьшей возможной черной дыры.
Основную роль в квантовой гравитации будет играть принцип неопределенности , где — гравитационный радиус , — радиальная координата , — планковская длина. Этот принцип неопределенности является еще одной формой принципа неопределенности Гейзенберга между импульсом и координатой применительно к шкале Планка . Действительно, это соотношение можно записать следующим образом:, где — гравитационная постоянная , — масса тела, — скорость света , — приведенная постоянная Планка . Сокращая одинаковые константы с двух сторон, мы получаем принцип неопределенности Гейзенберга . Принцип неопределенности предсказывает появление виртуальных черных дыр и кротовых нор ( квантовая пена ) в масштабах Планка . {2})}
{2})}
Видно, что на планковском масштабе метрика пространства-времени в специальной и общей теории относительности ограничена снизу планковской длиной (появляется деление на ноль), и на этом масштабе должны быть реальные и виртуальные черные дыры .
р знак равно ℓ п {\ displaystyle r = \ ell _ {P}}
Метрика пространства-времени колеблется и порождает квантовую пену . Эти флуктуации в макромире и в мире атомов очень малы по сравнению с и становятся заметными только в масштабах Планка. Лоренц-инвариантность нарушается на планковском масштабе. Формула для флуктуаций гравитационного потенциала согласуется с соотношением неопределенностей Бора — Розенфельда . Из-за малости значения формула для инвариантного интервала в специальной теории относительности всегда записывается в метрике Галилея , что на самом деле не соответствует действительности. Правильная формула должна учитывать флуктуации метрики пространства-времени и наличие виртуальных черных дыр и кротовых нор (квантовой пены) на расстояниях планковского масштаба. {- 5}} ( Δ р s > 0 ) {\ displaystyle (\ Delta r_ {s}> 0)}
{- 5}} ( Δ р s > 0 ) {\ displaystyle (\ Delta r_ {s}> 0)}
Любая попытка исследовать возможное существование более коротких расстояний путем столкновения с более высокими энергиями неизбежно приведет к образованию черных дыр. Столкновения более высоких энергий, вместо того, чтобы разделять материю на более мелкие части, просто породили бы большие черные дыры. Уменьшение приведет к увеличению и наоборот. Последующее увеличение энергии приведет к появлению более крупных черных дыр с худшим, а не лучшим разрешением. Следовательно, планковская длина — это минимальное расстояние, которое можно исследовать.
Δ р {\ displaystyle \ Delta r} Δ р s {\ displaystyle \ Delta r_ {s}}
Длина Планка относится к внутренней архитектуре частиц и объектов. Многие другие величины, имеющие единицы длины, могут быть намного короче планковской длины. Например, длина волны фотона может быть произвольно короткой: любой фотон может быть усилен, как гарантирует специальная теория относительности, так что его длина волны станет еще короче.
Планковскую длину иногда ошибочно принимают за минимальную длину пространства-времени, но это не принимается традиционной физикой, поскольку это потребовало бы нарушения или модификации симметрии Лоренца . Однако некоторые теории петлевой квантовой гравитации действительно пытаются установить минимальную длину в масштабе планковской длины, хотя не обязательно самой планковской длины, или пытаются установить планковскую длину как инвариантную для наблюдателя, известную как двойная специальная теория относительности .
Струны теории струн моделируются так, чтобы иметь порядок длины Планка. В теориях больших дополнительных измерений длина Планка не имеет фундаментального физического значения, а квантовые гравитационные эффекты проявляются в других масштабах.
Планковская длина и евклидова геометрия
Планковская длина — это длина, на которой квантовые нулевые колебания гравитационного поля полностью искажают евклидову геометрию . Гравитационное поле совершает нулевые колебания, и связанная с ним геометрия также колеблется. Отношение длины окружности к радиусу колеблется около евклидова значения. Чем меньше масштаб, тем больше отклонения от евклидовой геометрии. Оценим порядок длины волны нулевых гравитационных колебаний, при которой геометрия становится совершенно непохожей на геометрию Евклида. Степень отклонения геометрии от евклидовой геометрии в гравитационном поле определяется отношением гравитационного потенциала и квадратом скорости света : . Когда , геометрия близка к евклидовой геометрии; для , все сходства исчезают. Энергия колебания шкалы равна (где — порядок частоты колебаний). Гравитационный потенциал , созданный массой , при этом длина , где есть постоянная всемирного тяготения . Вместо , мы должны подставить массу, которая, согласно формуле Эйнштейна , соответствует энергии (где ). Получаем . Разделив это выражение на , получаем величину отклонения . Приравнивая , мы находим длину, на которой евклидова геометрия полностью искажается.
Гравитационное поле совершает нулевые колебания, и связанная с ним геометрия также колеблется. Отношение длины окружности к радиусу колеблется около евклидова значения. Чем меньше масштаб, тем больше отклонения от евклидовой геометрии. Оценим порядок длины волны нулевых гравитационных колебаний, при которой геометрия становится совершенно непохожей на геометрию Евклида. Степень отклонения геометрии от евклидовой геометрии в гравитационном поле определяется отношением гравитационного потенциала и квадратом скорости света : . Когда , геометрия близка к евклидовой геометрии; для , все сходства исчезают. Энергия колебания шкалы равна (где — порядок частоты колебаний). Гравитационный потенциал , созданный массой , при этом длина , где есть постоянная всемирного тяготения . Вместо , мы должны подставить массу, которая, согласно формуле Эйнштейна , соответствует энергии (где ). Получаем . Разделив это выражение на , получаем величину отклонения . Приравнивая , мы находим длину, на которой евклидова геометрия полностью искажается. {2}} л {\ displaystyle l} л {\ displaystyle l} ℓ п {\ displaystyle \ ell _ {P}}
{2}} л {\ displaystyle l} л {\ displaystyle l} ℓ п {\ displaystyle \ ell _ {P}}
Смотрите также
Рекомендации
Цитаты
Библиография
Внешние ссылки
Единицы Планка — Planck units
Набор единиц измерения, определенных исключительно в терминах универсальных физических констант, предложенных физиком Максом Планком.
В физике элементарных частиц и физической космологии , планковские единицы представляют собой совокупность единиц измерения , определенных исключительно в терминах четырех универсальных физических констант , таким образом , что эти физические константы принимают на численном значении 1 , когда выражена в терминах этих единиц.
Первоначально предложенные в 1899 году немецким физиком Максом Планком , эти единицы представляют собой систему естественных единиц, потому что происхождение их определения происходит только от свойств природы, а не от каких-либо человеческих построений . Единицы Планка — это только одна из нескольких систем естественных единиц, но единицы Планка основаны не на свойствах какого-либо объекта-прототипа или частицы (выбор которых по своей сути произвольный), а только на свойствах свободного пространства . Они актуальны при исследовании объединенных теорий, таких как квантовая гравитация .
Единицы Планка — это только одна из нескольких систем естественных единиц, но единицы Планка основаны не на свойствах какого-либо объекта-прототипа или частицы (выбор которых по своей сути произвольный), а только на свойствах свободного пространства . Они актуальны при исследовании объединенных теорий, таких как квантовая гравитация .
Термин масштаб Планка относится к количеству пространства, времени, энергии и других единиц, которые по величине аналогичны соответствующим единицам Планка. Эта область может характеризоваться энергиями около 10 19 ГэВ , время интервалы по всему 10 −43 с и длиной около 10 −35 м (приблизительно эквивалент энергии Планковской массы, Планковского времени и Планковской длины). В масштабе Планка не ожидается , что предсказания Стандартной модели , квантовой теории поля и общей теории относительности будут применяться, и ожидается, что квантовые эффекты гравитации будут преобладать. Самый известный пример — это условия в первые 10–43 секунды нашей Вселенной после Большого взрыва , примерно 13,8 миллиарда лет назад.
Самый известный пример — это условия в первые 10–43 секунды нашей Вселенной после Большого взрыва , примерно 13,8 миллиарда лет назад.
Четыре универсальные константы, которые по определению имеют числовое значение 1 при выражении в этих единицах:
Единицы Planck не учитывают электромагнитный размер. Некоторые авторы решили расширить систему до электромагнетизма, например, определив электрическую постоянную ε 0 как имеющую числовое значение 1 или 1/4 π в этой системе. Точно так же авторы предпочитают использовать варианты системы, которые присваивают другие числовые значения одной или нескольким из четырех констант, указанных выше.
Вступление
Любой системе измерения может быть назначен взаимно независимый набор основных величин и связанных с ними основных единиц , из которых могут быть выведены все другие величины и единицы. В Международной системе единиц , например, базовые величины СИ включают длину с соответствующей единицей измерения — метр . {2}}}.}
{2}}}.}
Это последнее уравнение (без G ) действительно только в том случае , если F , m 1 , m 2 и r — безразмерные числовые значения этих величин, измеренные в единицах Планка. Вот почему единицы Планка или любое другое использование натуральных единиц следует использовать с осторожностью. Ссылаясь на G = c = 1 , Пол С. Вессон писал, что «математически это приемлемый трюк, который экономит труд. Физически он представляет собой потерю информации и может привести к путанице».
История и определение
Концепция естественных единиц была введена в 1881 году, когда Джордж Джонстон Стоуни , отметив, что электрический заряд квантуется, производные единицы длины, времени и массы, теперь названы единицами Стони в его честь, путем нормализации G , c и заряда электрона. , e , к 1. В 1899 году, за год до появления квантовой теории, Макс Планк ввел то, что позже стало известно как постоянная Планка. В конце статьи он предложил базовые блоки, позже названные в его честь. Единицы Планка основаны на кванте действия, теперь обычно известном как постоянная Планка, который появился в приближении Вина для излучения черного тела . Планк подчеркнул универсальность новой системы единиц, написав:
В конце статьи он предложил базовые блоки, позже названные в его честь. Единицы Планка основаны на кванте действия, теперь обычно известном как постоянная Планка, который появился в приближении Вина для излучения черного тела . Планк подчеркнул универсальность новой системы единиц, написав:
… die Möglichkeit gegeben ist, Einheiten für Länge, Masse, Zeit und Temperatur aufzustellen, welche, unabhängig von speciellen Körpern oder Substanzen, ihre Bedeutung für alle Zeiten und daeßrlicten All, und auheßermersische Maßeinheiten «bezeichnet werden können .
… можно установить единицы измерения длины, массы, времени и температуры, которые не зависят от особых тел или веществ, обязательно сохраняя свое значение для всех времен и для всех цивилизаций, включая внеземные и нечеловеческие, которые могут называться «натуральными единицами измерения».
Планка рассматривать только единицы , основанные на универсальных констант , , и прибыть в естественных единицах для длины , времени , массы и температуры . {2}}}}}
{2}}}}}
В отличие от Международной системы единиц , не существует официального органа, который бы давал определение системе единиц Планка. Франк Вильчек и Бартон Цвибах определяют базовые единицы Планка как единицы массы, длины и времени, с учетом того, что дополнительная единица измерения температуры является избыточной. В других таблицах, помимо единицы температуры, добавляется единица электрического заряда, иногда при этом также заменяя массу энергией. В зависимости от выбора автора эта единица начисления определяется как
- q п знак равно 4 π ϵ 0 ℏ c {\ displaystyle q _ {\ text {P}} = {\ sqrt {4 \ pi \ epsilon _ {0} \ hbar c}}}
или же
- q п знак равно ϵ 0 ℏ c . {\ displaystyle q _ {\ text {P}} = {\ sqrt {\ epsilon _ {0} \ hbar c}}.}
Заряд Планка, а также другие электромагнитные единицы, которые можно определить как сопротивление и магнитный поток, труднее интерпретировать, чем оригинальные единицы Планка, и используются реже. Внутреннее предложение Рабочей группы SI от 2006 г. об установлении заряда Планка вместо элементарного заряда было отклонено, и вместо этого было выбрано фиксированное значение элементарного заряда по определению.
Внутреннее предложение Рабочей группы SI от 2006 г. об установлении заряда Планка вместо элементарного заряда было отклонено, и вместо этого было выбрано фиксированное значение элементарного заряда по определению.
В единицах СИ значения c , h , e и k B являются точными, а значения ε 0 и G в единицах СИ соответственно имеют относительную погрешность 1,5 × 10 −10 и 2,2 × 10 −5 . Следовательно, неопределенность в значениях СИ единиц Планка вывести почти полностью из неопределенности в значении СИ G .
Производные единицы
В любой системе измерения единицы для многих физических величин могут быть получены из основных единиц. В таблице 2 представлен образец производных единиц Планка, некоторые из которых на самом деле используются редко. Как и в случае с базовыми единицами, их использование в основном ограничивается теоретической физикой, потому что большинство из них слишком велики или слишком малы для эмпирического или практического использования, и в их значениях есть большие погрешности.
Некоторые единицы Планка, такие как время и длина, на много порядков слишком велики или слишком малы для практического использования, поэтому единицы Планка как система обычно имеют отношение только к теоретической физике. В некоторых случаях единица Планка может предлагать ограничение диапазона физической величины, в которой применяются современные теории физики. Например, наше понимание Большого взрыва начинается, когда Вселенная была старше одного планковского времени, а именно после эпохи Планка . Описание Вселенной в эпоху Планка требует теории квантовой гравитации , которая включала бы квантовые эффекты в общую теорию относительности . Такой теории пока не существует.
Некоторые величины не являются «экстремальными» по величине, например масса Планка, которая составляет около 22 микрограммов : очень велика по сравнению с субатомными частицами и находится в пределах диапазона масс живых существ; это может быть минимальная теоретическая масса черной дыры . Точно так же связанные единицы энергии и количества движения входят в диапазон некоторых повседневных явлений.
Точно так же связанные единицы энергии и количества движения входят в диапазон некоторых повседневных явлений.
Значимость
В единицах Планка мало антропоцентрического произвола, но они все же включают в себя произвольный выбор определяющих констант. В отличие от метра и секунды , которые существуют в качестве основных единиц в системе СИ по историческим причинам, планковская длина и планковское время концептуально связаны на фундаментальном физическом уровне. Следовательно, естественные единицы помогают физикам переосмыслить вопросы. Фрэнк Вильчек кратко об этом говорит:
Мы видим, что вопрос [поставлен] не в том, «Почему гравитация такая слабая?» скорее, «Почему масса протона такая мала?» Ибо в естественных (планковских) единицах сила гравитации — это просто то, что она есть, первичная величина, а масса протона — это крошечное число [1 / (13 квинтиллионов )].
Хотя это правда, что электростатическая сила отталкивания между двумя протонами (только в свободном пространстве) значительно превышает силу гравитационного притяжения между теми же двумя протонами, дело не в относительной силе двух фундаментальных сил. С точки зрения единиц Планка, это сравнение яблок с апельсинами , потому что масса и электрический заряд — несоизмеримые величины. Скорее, несоответствие величины силы является проявлением того факта, что заряд протонов приблизительно равен единице заряда, но масса протонов намного меньше единицы массы.
С точки зрения единиц Планка, это сравнение яблок с апельсинами , потому что масса и электрический заряд — несоизмеримые величины. Скорее, несоответствие величины силы является проявлением того факта, что заряд протонов приблизительно равен единице заряда, но масса протонов намного меньше единицы массы.
Планковская шкала
В физике элементарных частиц и физической космологии масштаб Планка — это шкала энергии около 1,22 × 10 19 ГэВ (энергия Планка, соответствующая эквивалентности массы Планка по энергии , 2,176 45 × 10 -8 кг ) , при котором квантовые эффекты от тяжести стать сильными. В этом масштабе нынешние описания и теории взаимодействий субатомных частиц в терминах квантовой теории поля рушатся и становятся неадекватными из-за воздействия очевидной неперенормируемости гравитации в рамках текущих теорий.
Отношение к гравитации
В масштабе длины Планка ожидается, что сила гравитации станет сопоставимой с другими силами, и предполагается, что все фундаментальные силы объединены в этом масштабе, но точный механизм этого объединения остается неизвестным. Таким образом, масштаб Планка — это точка, где эффекты квантовой гравитации больше нельзя игнорировать в других фундаментальных взаимодействиях , и где текущие расчеты и подходы начинают ломаться, и требуются средства для учета ее воздействия.
Таким образом, масштаб Планка — это точка, где эффекты квантовой гравитации больше нельзя игнорировать в других фундаментальных взаимодействиях , и где текущие расчеты и подходы начинают ломаться, и требуются средства для учета ее воздействия.
Хотя физики достаточно хорошо понимают другие фундаментальные взаимодействия сил на квантовом уровне, гравитация проблематична и не может быть интегрирована с квантовой механикой при очень высоких энергиях с использованием обычных рамок квантовой теории поля. На меньших уровнях энергии его обычно игнорируют, в то время как для энергий, приближающихся или превышающих планковский масштаб, требуется новая теория квантовой гравитации . Другие подходы к этой проблеме включают теорию струн и М-теорию , петлевую квантовую гравитацию , некоммутативную геометрию , масштабную относительность , теорию причинных множеств и p- адическую квантовую механику .
В космологии
В космологии Большого Взрыва , то эпоха Планка или Планка эпохи является самым ранним этапом Большого взрыва , до того , как прошло время был равен времени Планка, т P , или приблизительно 10 -43 секунд. В настоящее время нет доступной физической теории для описания таких коротких времен, и неясно, в каком смысле понятие времени имеет смысл для значений, меньших, чем время Планка. Обычно считается, что квантовые эффекты гравитации доминируют над физическими взаимодействиями в этом масштабе времени. В этом масштабе, единая сила в стандартной модели предполагается , должны быть объединены с гравитацией . Неизмеримо горячее и плотное состояние эпохи Планка сменилось эпохой великого объединения , когда гравитация отделена от единой силы Стандартной модели, за которой, в свою очередь, последовала инфляционная эпоха , которая закончилась примерно через 10-32 секунды (или около 10 10 т П ).
В настоящее время нет доступной физической теории для описания таких коротких времен, и неясно, в каком смысле понятие времени имеет смысл для значений, меньших, чем время Планка. Обычно считается, что квантовые эффекты гравитации доминируют над физическими взаимодействиями в этом масштабе времени. В этом масштабе, единая сила в стандартной модели предполагается , должны быть объединены с гравитацией . Неизмеримо горячее и плотное состояние эпохи Планка сменилось эпохой великого объединения , когда гравитация отделена от единой силы Стандартной модели, за которой, в свою очередь, последовала инфляционная эпоха , которая закончилась примерно через 10-32 секунды (или около 10 10 т П ).
Наблюдаемая Вселенная сегодня выражается в единицах Планка:
| Собственность современной наблюдаемой Вселенной | Приблизительное количество единиц Планка | Эквиваленты |
|---|---|---|
| Возраст | 8,08 × 10 60 т П | 4,35 × 10 17 с, или 13,8 × 10 9 лет |
| Диаметр | 5,4 × 10 61 л П | 8,7 × 10 26 м или 9,2 × 10 10 световых лет |
| Масса | ок. 10 60 м P 10 60 м P | 3 × 10 52 кг или 1,5 × 10 22 массы Солнца (только с учетом звезд) 10 80 протонов (иногда известное как число Эддингтона ) |
| Плотность | 1,8 × 10 −123 м P ⋅ l P −3 | 9,9 × 10 −27 кг⋅м −3 |
| Температура | 1.9 × 10 −32 Т П | 2.725 K температура космического микроволнового фонового излучения |
| Космологическая постоянная | 2,9 × 10 −122 л −2 P | 1,1 × 10 −52 м −2 |
| Постоянная Хаббла | 1,18 × 10 −61 т −1 P | 2,2 × 10 −18 с −1 или 67,8 (км / с) / Мпк |
После измерения космологической постоянной в 1998 году, оцененной в 10 −122 в единицах Планка, было отмечено, что это предположительно близко к обратной величине квадрата возраста Вселенной . {3}}}}}
{3}}}}}
Это равно 1,616 255 (18) × 10 -35 м , где две цифры, заключенные в круглые скобки, представляют собой расчетную стандартную ошибку, связанную с сообщенным числовым значением.
Единица времени Планка — это время, необходимое свету, чтобы пройти расстояние в 1 планковскую длину в вакууме , что составляет временной интервал приблизительно 5,39 × 10 −44 с . Все научные эксперименты и человеческий опыт происходят в масштабах времени, которые на много порядков больше планковского времени, поэтому любые события, происходящие в масштабе Планка, невозможно обнаружить с помощью современных научных технологий. По состоянию на октябрь 2020 года наименьшая неопределенность временного интервала при прямых измерениях составляла порядка 247 зептосекунд ( 2,47 × 10 −19 с ).
Хотя в настоящее время нет известного способа измерения временных интервалов в масштабе планковского времени, исследователи в 2020 году предложили теоретический аппарат и эксперимент, которые, если они когда-либо будут реализованы, могут быть подвержены влиянию таких коротких эффектов времени, как 10 −33. секунд, тем самым устанавливая верхний обнаруживаемый предел для квантования времени, который примерно в 20 миллиардов раз длиннее планковского времени.
секунд, тем самым устанавливая верхний обнаруживаемый предел для квантования времени, который примерно в 20 миллиардов раз длиннее планковского времени.
Планковская энергия
Большинство планковских единиц чрезвычайно малы, как в случае планковской длины или планковского времени, или чрезвычайно велики, как в случае планковской температуры или планковского ускорения. Для сравнения: энергия Планка примерно равна энергии, запасенной в автомобильном бензобаке (57,2 л бензина при 34,2 МДж / л химической энергии). Космических лучей сверхвысокой энергии наблюдалась в 1991 году было измерено энергию около 50 Дж, что эквивалентно примерно 2,5 × 10 -8 Е Р .
Сила Планка
Сила Планка — это производная единица силы, полученная в результате определения базовых единиц Планка для времени, длины и массы. Он равен естественной единице количества движения, деленной на естественную единицу времени. {44} {\ mbox {N.}}}
{44} {\ mbox {N.}}}
Сила гравитационного притяжения двух тел массой 1 Планка каждое, разделенных на 1 длину Планка, равна 1 силе Планка; эквивалентно, электростатическая сила притяжения / отталкивания двух планковских зарядов, разнесенных на 1 планковскую длину, равна 1 планковской силе.
Различные авторы утверждали, что сила Планка порядка максимальной силы, которую можно наблюдать в природе. Однако справедливость этих предположений оспаривается.
Планковский импульс
Этот график зависимости кинетической энергии от количества движения имеет место для большинства движущихся объектов, встречающихся в повседневной жизни. Он показывает объекты с одинаковой кинетической энергией (горизонтально связанные), которые несут разное количество импульса, а также то, как скорость маломассивного объекта сравнивается (путем вертикальной экстраполяции) со скоростью после совершенно неупругого столкновения с большим объектом в состоянии покоя. . Линии с большим уклоном (подъем / ход = 2) обозначают контуры постоянной массы, а линии единичного уклона обозначают контуры постоянной скорости. График также показывает, где фигурируют скорость света, постоянная Планка и kT (Примечание: линия с надписью Вселенная отслеживает только оценку массы видимой Вселенной).
График также показывает, где фигурируют скорость света, постоянная Планка и kT (Примечание: линия с надписью Вселенная отслеживает только оценку массы видимой Вселенной).
Импульс Планка равен массе Планка, умноженной на скорость света . В отличие от большинства других единиц Планка, импульс Планка возникает в человеческом масштабе. Для сравнения, бег с пятифунтовым объектом (10 8 × масса Планка) со средней скоростью бега (10 -8 × скорость света в вакууме) дал бы объекту планковский импульс. Человек весом 70 кг, движущийся со средней скоростью ходьбы 1,4 м / с (5,0 км / ч; 3,1 мили в час), будет иметь импульс около 15 . Бейсбол , который имеет массу 0,145 кг, путешествия при 45 м / с (160 км / ч; 100 миль / ч) будет иметь импульс Планка.
м п c {\ displaystyle m _ {\ text {P}} c} м знак равно {\ displaystyle m =}
Планковская температура
Планковская температура 1 (единица), равная 1,416 784 (16) × 10 32 К , считается фундаментальным пределом температуры. Объект с температурой 1,42 × 10 32 Кельвина ( Т Р ) будет испускать излучение абсолютно черного тела с пиковой длиной волны от 1,616 × 10 -35 м ( планковская длина ), где каждый фотон и каждое отдельное столкновение будут иметь энергию для создания планковской частицы . Там нет известных физических моделей в состоянии описать температуры больше чем или равна T P .
Объект с температурой 1,42 × 10 32 Кельвина ( Т Р ) будет испускать излучение абсолютно черного тела с пиковой длиной волны от 1,616 × 10 -35 м ( планковская длина ), где каждый фотон и каждое отдельное столкновение будут иметь энергию для создания планковской частицы . Там нет известных физических моделей в состоянии описать температуры больше чем или равна T P .
Список физических уравнений
Физические величины, которые имеют разные размеры (такие как время и длина), не могут быть приравнены, даже если они численно равны (1 секунда не то же самое, что 1 метр). В теоретической физике, однако, эту осторожность можно устранить с помощью процесса, называемого обезразмериванием . Таблица 3 показывает, как использование единиц Планка упрощает многие фундаментальные уравнения физики, потому что это дает каждой из пяти фундаментальных констант и их произведению простое числовое значение 1 . {2} \;}
{2} \;}
энтропии Больцмана
 {2}}} \ left ({\ frac {1} {\ epsilon _ {0}}} \ mathbf {J} + {\ frac {\ partial \ mathbf {E}} {\ partial t}} \ right)}
{2}}} \ left ({\ frac {1} {\ epsilon _ {0}}} \ mathbf {J} + {\ frac {\ partial \ mathbf {E}} {\ partial t}} \ right)} ∇ ⋅ B знак равно 0 {\ Displaystyle \ набла \ cdot \ mathbf {B} = 0 \}
∇ × E знак равно — ∂ B ∂ т {\ displaystyle \ nabla \ times \ mathbf {E} = — {\ frac {\ partial \ mathbf {B}} {\ partial t}}}
∇ × B знак равно 4 π J + ∂ E ∂ т {\ displaystyle \ nabla \ times \ mathbf {B} = 4 \ pi \ mathbf {J} + {\ frac {\ partial \ mathbf {E}} {\ partial t}}}
Альтернативные варианты нормализации
Как уже указывалось выше, единицы Планка выводятся путем «нормализации» числовых значений некоторых фундаментальных констант к 1. Эти нормализации не являются единственно возможными и не обязательно лучшими. Более того, выбор факторов для нормализации среди факторов, фигурирующих в фундаментальных уравнениях физики, не очевиден, и значения единиц Планка чувствительны к этому выбору.
Эти нормализации не являются единственно возможными и не обязательно лучшими. Более того, выбор факторов для нормализации среди факторов, фигурирующих в фундаментальных уравнениях физики, не очевиден, и значения единиц Планка чувствительны к этому выбору.
Множитель 4 π широко используется в теоретической физике, потому что площадь поверхности сферы радиуса r равна 4 π r 2 в контекстах, имеющих сферическую симметрию в трех измерениях. Это, наряду с понятием потока , является основой для закона обратных квадратов , закона Гаусса , и дивергенции оператора , приложенного к плотности потока . Например, гравитационные и электростатические поля, создаваемые точечными зарядами, обладают сферической симметрией (Barrow 2002: 214–15). Например, 4 π r 2, появляющееся в знаменателе закона Кулона в рационализированной форме , следует из потока электростатического поля, равномерно распределенного по поверхности сферы.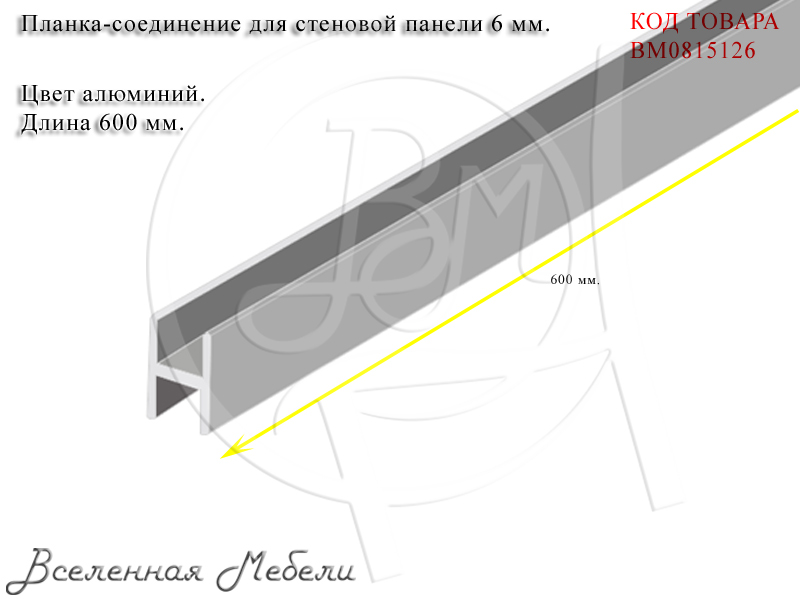 То же самое и с законом всемирного тяготения Ньютона. (Если бы пространство имело более трех пространственных измерений, коэффициент 4 π был бы изменен в соответствии с геометрией сферы в более высоких измерениях .)
То же самое и с законом всемирного тяготения Ньютона. (Если бы пространство имело более трех пространственных измерений, коэффициент 4 π был бы изменен в соответствии с геометрией сферы в более высоких измерениях .)
Следовательно, значительная часть физической теории, разработанная после того, как Планк (1899) предлагает нормировать не G, а либо 4 π G (или 8 π G, или 16 π G ) на 1. Это приведет к увеличению множителя 1 / 4 π (или же 1 / 8 π или же 1 / 16 π ) в безразмерную форму закона всемирного тяготения, совместимую с современной рационализированной формулировкой закона Кулона в терминах диэлектрической проницаемости вакуума. Фактически, альтернативные нормализации часто сохраняют фактор 1 / 4 π в безразмерной форме закона Кулона, так что безразмерные уравнения Максвелла для электромагнетизма и гравитоэлектромагнетизма принимают ту же форму, что и для электромагнетизма в SI, которые не имеют никаких множителей 4 π . Когда это применяется к электромагнитным постоянным, ε 0 , эта система единиц называется « рационализированной » . Применительно к единицам гравитации и Планка они называются рационализированными единицами Планка и используются в физике высоких энергий.
Когда это применяется к электромагнитным постоянным, ε 0 , эта система единиц называется « рационализированной » . Применительно к единицам гравитации и Планка они называются рационализированными единицами Планка и используются в физике высоких энергий.
Рационализированные единицы Планка определены так, что .
c знак равно 4 π грамм знак равно ℏ знак равно ε 0 знак равно k B знак равно 1 {\ displaystyle c = 4 \ pi G = \ hbar = \ varepsilon _ {0} = k _ {\ text {B}} = 1}
Есть несколько возможных альтернативных нормализаций.
Гравитационная постоянная
В 1899 году закон всемирного тяготения Ньютона все еще рассматривался как точный, а не как удобное приближение для «малых» скоростей и масс (приблизительный характер закона Ньютона был показан после развития общей теории относительности в 1915 году). Следовательно, Планк нормализовал к 1 гравитационную постоянную G в законе Ньютона. В теориях, появившихся после 1899 года, G почти всегда появляется в формулах, умноженных на 4 π или их небольшое целое число. Следовательно, выбор, который следует сделать при разработке системы естественных единиц, состоит в том, что, если таковые имеются, случаи 4 π, появляющиеся в уравнениях физики, должны быть исключены с помощью нормализации.
В теориях, появившихся после 1899 года, G почти всегда появляется в формулах, умноженных на 4 π или их небольшое целое число. Следовательно, выбор, который следует сделать при разработке системы естественных единиц, состоит в том, что, если таковые имеются, случаи 4 π, появляющиеся в уравнениях физики, должны быть исключены с помощью нормализации.
- Нормализация 4 π G до 1 (и, следовательно, установка G = 1 / 4π ):
- Положив 8 π G = 1 (и, следовательно, установив G = 1 / 8π ). Это исключит 8 П G из уравнений поля Эйнштейна , Эйнштейн-Гильберт действия , и уравнений Фридмана , для гравитации. Единицы Планка, модифицированные так, что 8 π G = 1 , известны как уменьшенные единицы Планка , потому что масса Планка делится на √ 8 π . Кроме того , формула Бекенштейн-Хокинга для энтропии черной дыры упрощается до S BH = ( м ВН ) 2 /2 = 2 & pi ; A BH .

- Установка 16 π G = 1 (и, следовательно, установка G = 1 / 16π ). Это устранило бы постоянную в 4 / 16 π G из действия Эйнштейна – Гильберта. Форма уравнений поля Эйнштейна с космологической постоянной Λ принимает вид R μν — 1 / 2 Rg μν + Λ g μν = 1 / 2 Т µν .
Единицы Планка и инвариантное масштабирование природы
Некоторые теоретики (такие как Дирак и Милн ) предложили космологии, которые предполагают, что физические «константы» могут действительно изменяться со временем (например, переменная скорость света или теория переменного G Дирака ). Такие космологии не получили широкого признания, и все же существует значительный научный интерес к возможности того, что физические «константы» могут измениться, хотя такие предложения вызывают сложные вопросы. Возможно, первый вопрос, на который нужно ответить, звучит так: как такое изменение повлияет на работу физических измерений или, что более фундаментально, на наше восприятие реальности? Если бы какая-то конкретная физическая константа изменилась, как бы мы это заметили или чем изменилась бы физическая реальность? Какие измененные константы приводят к значимой и измеримой разнице в физической реальности? Если физическая константа , которая не безразмерная , такие как скорость света , сделала в изменении действительности, мы могли бы заметить или измерить его однозначно? — вопрос, рассмотренный Майклом Даффом в его статье «Комментарий к изменению во времени фундаментальных констант».
Возможно, первый вопрос, на который нужно ответить, звучит так: как такое изменение повлияет на работу физических измерений или, что более фундаментально, на наше восприятие реальности? Если бы какая-то конкретная физическая константа изменилась, как бы мы это заметили или чем изменилась бы физическая реальность? Какие измененные константы приводят к значимой и измеримой разнице в физической реальности? Если физическая константа , которая не безразмерная , такие как скорость света , сделала в изменении действительности, мы могли бы заметить или измерить его однозначно? — вопрос, рассмотренный Майклом Даффом в его статье «Комментарий к изменению во времени фундаментальных констант».
Джордж Гамов в своей книге « Мистер Томпкинс в стране чудес» утверждал, что достаточное изменение размерной физической постоянной, такой как скорость света в вакууме, приведет к очевидным ощутимым изменениям. Но эта идея подвергается сомнению:
[] Важный урок, который мы извлекаем из того, как чистые числа, такие как α, определяют мир, — это то, что на самом деле означает для миров быть разными.
Чистое число, которое мы называем постоянной тонкой структуры и обозначаем α, представляет собой комбинацию заряда электрона e , скорости света c и постоянной Планка h . Сначала у нас может возникнуть соблазн подумать, что мир, в котором скорость света меньше, будет другим миром. Но это было бы ошибкой. Если бы все c , h и e были изменены так, чтобы их значения в метрических (или любых других) единицах были другими, когда мы искали их в наших таблицах физических констант, но значение α осталось прежним, этот новый мир было бы неотличимо от нашего мира с точки зрения наблюдения . Единственное, что имеет значение при определении миров, — это значения безразмерных констант Природы. Если бы все массы были удвоены по величине [включая массу Планка m P ], вы не можете сказать, потому что все чистые числа, определяемые отношениями любой пары масс, не изменились.
- Курган 2002
Ссылаясь на «Комментарий к изменению фундаментальных констант во времени» и на статью Даффа, Окуна и Венециано «Триалог по количеству фундаментальных констант», в частности на раздел, озаглавленный «Оперативно неразличимый мир мистера Томпкинса», если все физические величины (массы и другие свойства частиц) были выражены в единицах Планка, эти величины будут безразмерными числами (масса, деленная на массу Планка, длина, деленная на длину Планка, и т. д.) и единственными величинами, которые мы в конечном итоге измеряем. в физических экспериментах или в нашем восприятии реальности — безразмерные числа. Когда кто-то обычно измеряет длину с помощью линейки или рулетки, этот человек на самом деле считает отметки на данном эталоне или измеряет длину относительно этого эталона, который является безразмерным значением. То же самое и с физическими экспериментами, поскольку все физические величины измеряются относительно некоторой другой величины аналогичного размера.
Мы можем заметить разницу, если изменится некоторая безразмерная физическая величина, такая как постоянная тонкой структуры , α , или отношение масс протона к электрону , м п / м е , изменяется (атомная структура изменилась бы), но если бы все безразмерные физические величины остались неизменными (это включает все возможные отношения одинаковых физических величин), мы не сможем сказать , изменилась ли размерная величина, такая как скорость света , c . И действительно, концепция Томпкинса теряет смысл в нашем восприятии реальности, если размерная величина, такая как c , изменилась , даже резко.
Если бы скорость света c как-нибудь внезапно уменьшилась вдвое и изменилась на 1 / 2 c (но с аксиомой, что все безразмерные физические величины остаются прежними), то планковская длина увеличилась бы в 2 √ 2 раза с точки зрения какого-нибудь незатронутого наблюдателя снаружи. {2}}} = {\ frac {m _ {\ text { P}}} {m_ {e} \ alpha}} l _ {\ text {P}}.}
{2}}} = {\ frac {m _ {\ text { P}}} {m_ {e} \ alpha}} l _ {\ text {P}}.}
Тогда атомы были бы больше (в одном измерении) на 2 √ 2 , каждый из нас был бы выше на 2 √ 2 , и поэтому наши измерительные стержни были бы выше (и шире и толще) в 2 √ 2 раза . Наше восприятие расстояния и длины относительно длины Планка по аксиоме является неизменной безразмерной константой.
Наши часы будут идти медленнее в 4 √ 2 раза (с точки зрения этого незатронутого наблюдателя снаружи), потому что время Планка увеличилось на 4 √ 2, но мы не заметили бы разницы (наше восприятие продолжительности времени относительно планковского времени является по аксиоме неизменной безразмерной константой). Этот гипотетический незатронутый наблюдатель снаружи мог бы заметить, что теперь свет распространяется со скоростью вдвое меньшей, чем раньше (а также со всеми другими наблюдаемыми скоростями), но он все равно будет двигаться. 299 792 458 наших новых метров за время, прошедшее до одной из наших новых секунд ( 1 / 2 c × 4 √ 2 ÷ 2 √ 2 продолжает равняться 299 792 458 м / с ). Мы не заметим никакой разницы.
Мы не заметим никакой разницы.
Это противоречит тому, что пишет Джордж Гамов в своей книге « Мистер Томпкинс» ; там Гамов предполагает, что если бы универсальная константа, зависящая от размерности, такая как c, значительно изменилась, мы бы легко заметили разницу. Несогласие лучше рассматривать как двусмысленность фразы «изменение физической константы» ; что произойдет, зависит от того, (1) все ли другие безразмерные константы остались прежними, или (2) все остальные зависящие от размеров константы остались прежними. Второй выбор — это несколько сбивающая с толку возможность, поскольку большинство наших единиц измерения определяется в зависимости от результатов физических экспериментов, а экспериментальные результаты зависят от констант. Гамов не обращает внимания на эту тонкость; мысленные эксперименты, которые он проводит в своих популярных работах, предполагают второй вариант «изменения физической константы» . И Дафф или Барроу указали бы, что приписывание изменения измеряемой реальности, то есть α , определенной размерной составляющей величине, такой как c , неоправданно. Та же самая операционная разница в измерении или воспринимаемой реальности может быть также вызвана изменением h или e, если изменяется α и никакие другие безразмерные константы не изменяются. В определении миров в конечном итоге имеют значение только безразмерные физические константы.
И Дафф или Барроу указали бы, что приписывание изменения измеряемой реальности, то есть α , определенной размерной составляющей величине, такой как c , неоправданно. Та же самая операционная разница в измерении или воспринимаемой реальности может быть также вызвана изменением h или e, если изменяется α и никакие другие безразмерные константы не изменяются. В определении миров в конечном итоге имеют значение только безразмерные физические константы.
Этот неизменный аспект шкалы относительно Планка или любой другой системы естественных единиц приводит многих теоретиков к выводу, что гипотетическое изменение размерных физических констант может проявляться только как изменение безразмерных физических констант . Одной из таких безразмерных физических констант является постоянная тонкой структуры . Некоторые физики-экспериментаторы утверждают, что они действительно измерили изменение постоянной тонкой структуры, и это усилило споры об измерении физических констант. По мнению некоторых теоретиков, существуют некоторые очень особые обстоятельства, при которых изменения постоянной тонкой структуры можно измерить как изменение размерных физических констант. Другие, однако, отвергают возможность измерения изменения размерных физических констант при любых обстоятельствах. Сложность или даже невозможность измерения изменений размерных физических констант заставила некоторых теоретиков спорить друг с другом о том, имеет ли размерная физическая константа какое-либо практическое значение, и это, в свою очередь, приводит к вопросам о том, какие размерные физические константы имеют смысл.
По мнению некоторых теоретиков, существуют некоторые очень особые обстоятельства, при которых изменения постоянной тонкой структуры можно измерить как изменение размерных физических констант. Другие, однако, отвергают возможность измерения изменения размерных физических констант при любых обстоятельствах. Сложность или даже невозможность измерения изменений размерных физических констант заставила некоторых теоретиков спорить друг с другом о том, имеет ли размерная физическая константа какое-либо практическое значение, и это, в свою очередь, приводит к вопросам о том, какие размерные физические константы имеют смысл.
Смотрите также
Заметки
Рекомендации
Цитаты
Источники
- Барроу, Джон Д. (2002). Константы природы; От Альфы до Омеги — числа, в которых закодированы самые глубокие секреты Вселенной . Нью-Йорк: Книги Пантеона. ISBN 978-0-375-42221-8 . Полегче.

- Барроу, Джон Д .; Типлер, Фрэнк Дж. (1986). Антропный космологический принцип . Оксфорд: Claredon Press. ISBN 978-0-19-851949-2 . Сильнее.
- Пенроуз, Роджер (2005). «Раздел 31.1». Дорога к реальности . Нью-Йорк: Альфред А. Кнопф. ISBN 978-0-679-45443-4 .
- Планк, Макс (1899). «Убер необратимый Strahlungsvorgänge» . Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin (на немецком языке). 5 : 440–480. На стр. 478–80 впервые появляются базовые единицы Планка, отличные от заряда Планка , и постоянная Планка, которую Планк обозначил буквой b . a и f в этой статье соответствуют k и G в этой записи.
- Томилин, К.А. (1999). Естественные системы единиц: к столетнему юбилею системы Планка (PDF) . Материалы XXII семинара по физике высоких энергий и теории поля.
 С. 287–296. Архивировано из оригинального (PDF) 17 июня 2006 года.
С. 287–296. Архивировано из оригинального (PDF) 17 июня 2006 года.
Внешние ссылки
Планковские единицы — экстремальные величины
Макс Планк по праву считается великим физиком. Он стал основателем квантовой физики, работал в области термодинамики, поддерживал и разрабатывал специальную теорию относительности Эйнштейна. Фундаментальные величины, которыми пользуются ныне, тоже его заслуга. Постоянная Планка, открытие квантов и ещё много иных научных достижений привели учёного к закономерному итогу – Нобелевской премии. Занятия наукой не мешали ему быть человеком остроумным. Например, он всерьёз доказывал, что у чайной чашки есть две ручки, но они развёрнуты на 360о. А его замечание о том, что торжество истины приходит по мере вымирания её противников, так близко пониманию многих.
Планковские величины
Эти величины были обнародованы Планком 18 мая 1899 года. Учёный предложил систему «естественных единиц измерений», которая была основана на четырёх универсальных постоянных:
- Скорость света
- Гравитационная постоянная
- Постоянная Планка
- Постоянная Больцмана
Планковская длина
В Международной системе единиц (СИ) значение такого параметра определено примерно в 1,6 . 10-35 м. В эту естественную единицу вошли фундаментальные константы: скорость света, постоянная Планка, гравитационная постоянная. Наблюдаемая Вселенная имеет приблизительный радиус, равный 4,6 .1061 планковских длин.
10-35 м. В эту естественную единицу вошли фундаментальные константы: скорость света, постоянная Планка, гравитационная постоянная. Наблюдаемая Вселенная имеет приблизительный радиус, равный 4,6 .1061 планковских длин.
Измерение объектов с точностью, превосходящей длину системы единиц Планка, невозможно, поэтому представления о пространстве на меньших расстояниях неприменимы. По такой же причине нереально обнаружить дополнительные измерения, которые наличествуют в теории струн, так как они свёрнуты до параметров таких длин. Планковская длина считается предельным значением расстояния. Ниже этого предела само понятие длины перестаёт существовать, впрочем, как и пространство.
Планковское время
Эта единица имеет размерность времени и состоит из произведения фундаментальных констант. В физическом смысле – это время, необходимое частице, двигающейся со скоростью света, на преодоление планковской длины. Результатом Большого взрыва стало расширение пространства-времени из бесконечно малой точки. По прошествии одной такой единицы времени, гравитационные силы начинают отделяться от всех остальных сил. То время, что прошло после Большого взрыва, определяется в параметре 4,3 . 1017 с, что равно 8 .1060 планковских времён. На нынешний момент минимальный отрезок времени, доступный наблюдению, составил около аттосекунды, или 1026 величин времени Планка.
По прошествии одной такой единицы времени, гравитационные силы начинают отделяться от всех остальных сил. То время, что прошло после Большого взрыва, определяется в параметре 4,3 . 1017 с, что равно 8 .1060 планковских времён. На нынешний момент минимальный отрезок времени, доступный наблюдению, составил около аттосекунды, или 1026 величин времени Планка.
Планковская температура
Для современной физической теории невозможна величина температуры выше планковского значения. При параметрах больших энергия частиц увеличивается так сильно, что связывающие их силы сравниваются с остальными взаимодействиями. Такую температуру имела Вселенная в планковское время после Большого взрыва. Значение её непредставимо – 1,41679(11) . 1032 К (141 нониллион 679 октиллионов кельвинов).
Планковская масса
Планковская масса — величина минимальной массы чёрной дыры или максимально тяжелой элементарной частицы. Эта величина выделяется из других единиц Планка тем, что масштаб её более понятен. Поскольку значение её 2,176 . 10-8 кг (дли физики элементарных частиц – 2,43 . 1018 ГэВ/с2), она подходит для взвешивания ощутимых объектов. Например, блоха будет иметь массу в пределах от 4000 до 5000 планковских масс. Предложена гипотетическая частица, наделённая подобной массой – максимон. Такие частицы могут обладать электрическим зарядом, а могут оставаться нейтральными. Внутренняя температура их может быть предельно большой, или же они могут оставаться холодными.
Эта величина выделяется из других единиц Планка тем, что масштаб её более понятен. Поскольку значение её 2,176 . 10-8 кг (дли физики элементарных частиц – 2,43 . 1018 ГэВ/с2), она подходит для взвешивания ощутимых объектов. Например, блоха будет иметь массу в пределах от 4000 до 5000 планковских масс. Предложена гипотетическая частица, наделённая подобной массой – максимон. Такие частицы могут обладать электрическим зарядом, а могут оставаться нейтральными. Внутренняя температура их может быть предельно большой, или же они могут оставаться холодными.
Планковский заряд
Эта единица является одной из основных в планковской системе. Она выражается количеством электрического заряда, который определён терминами фундаментальных констант. Значение этой единицы 1,87554 . 10-18 кулон. Этот заряд по модулю превышает заряд электрона примерно в 11,706 раза.
Планковская плотность
За единицу плотности в этой системе принята плотность Вселенной по завершении планковской эпохи после Большого взрыва. Величина этого параметра огромна. Она сопоставима с 1023 масс Солнца, которые сжали в пространстве до размера ядра атома. Это значение является предельной плотностью для материи.
Величина этого параметра огромна. Она сопоставима с 1023 масс Солнца, которые сжали в пространстве до размера ядра атома. Это значение является предельной плотностью для материи.
Планковская эпоха
С именем Планка связаны многие величины и законы. В частности, физическая космология называет его именем эпоху самого раннего периода истории наблюдаемой нами Вселенной. Этот непродолжительный период, по теоретическим предположениям, продолжался в течение планковского времени, имеющего значение от 0 до 10-43секунд. В эту эпоху – около 13,8 млрд. лет назад – всё вещество Вселенной обладало энергией порядка 1019 ГэВ и было сосредоточено в одной точке. Радиус этой точки имел значение ~10−35 м, плотность ~1097 кг/м3, а температура ~1032 К. Поскольку размеры Вселенной были исключительно малы, случилось преобладание квантовых эффектов гравитации над физическими взаимодействиями. Невероятные значения температуры и плотности делали вещество неустойчивым. Произошло нарушение симметрии, что привело к проявлению фундаментальных сил – гравитационное воздействие отделилось от других фундаментальных взаимодействий.
Поскольку размеры Вселенной были исключительно малы, случилось преобладание квантовых эффектов гравитации над физическими взаимодействиями. Невероятные значения температуры и плотности делали вещество неустойчивым. Произошло нарушение симметрии, что привело к проявлению фундаментальных сил – гравитационное воздействие отделилось от других фундаментальных взаимодействий.
Постоянная Планка
Постоянная (квант действия) считается основной константой квантовой теории. Она является коэффициентом, связывающим количество энергии кванта электромагнитного излучения и его частоту. Это же справедливо для любых линейных колебательных физических систем и их частот. Параметр этой постоянной переопределён в 2011 году, и теперь она имеет значение 6,62606Х . 10-34 Дж.с. Символ «Х» поставлен вместо одной или нескольких значимых цифр, которые определятся в дальнейшем с большей точностью. Предназначением постоянной Планка является связывание двух систем единиц – квантовой и традиционной.
Планковские чёрные дыры
Этот тип чёрной дыры пока гипотетичен, но если они существуют, минимальная масса их должна быть равна планковской массе. Этот объект соответствует предполагаемому максимону, частице с такой же массой. Вероятно, что эта гипотетическая чёрная дыра – конечный продукт жизни обычной чёрной дыры. Она должна быть стабильна и не иметь излучения Хокинга. Плотность такого объекта будет выражаться значением порядка 1094 кг/м3 . Такие масштабы физики станет описывать квантовая гравитация, если учёные смогут разработать надлежащие теории.
На границе XX и XXI веков началась революция перехода метрологии в квантовую стадию. Она не в полном объёме основана на планковской системе, но всё-таки стоит на её фундаменте. Именно планковские единицы являются определяющими для применения современных физических теорий. Вдумываясь в значения планковских величин, невольно пытаешься представить эти невероятные массы и расстояния, плотности и время. Это очень сложно, практически нереально, но желание проникнуть в тайны природы всегда озаряло человеческую мысль…
Это очень сложно, практически нереально, но желание проникнуть в тайны природы всегда озаряло человеческую мысль…
Планковская длина — это… Что такое Планковская длина?
Планковская длина (обозначаемая ) — фундаментальная единица длины в планковской системе единиц, равная в системе СИ примерно 1,6·10−35 метров. Планковская длина — естественная единица длины, поскольку в неё входят только фундаментальные константы: скорость света, постоянная Планка и гравитационная постоянная.
Планковская длина равна:
- м,
где:
Две последние цифры в скобках означают неопределённость (стандартное отклонение) последних двух разрядов.
В системе единиц СИ примерный радиус наблюдаемой Вселенной (1,3·1026м или 13 миллиардов световых лет) равен 4,6·1061 планковских длин.
С точностью до множителя π, планковская масса равна массе чёрной дыры, радиус Шварцшильда которой равен её комптоновской длине волны. Радиус такой чёрной дыры будет по порядку величины равен планковской длине.
Простой анализ размерностей показывает, что измерение положения физических объектов с точностью до планковской длины проблематично. Действительно, проведём следующий мысленный эксперимент. Допустим, мы хотим определить положение объекта и посылаем на него поток электромагнитного излучения, то есть фотоны. Чем больше энергия фотонов, тем короче их длина волны и тем более точным будет измерение. Если бы фотон имел энергию, достаточную для измерения объектов размером с планковскую длину, он бы сколлапсировал в микроскопическую чёрную дыру и провести измерение было бы невозможно, таким образом, планковская длина накладывает фундаментальные ограничения на точность измерения длины.
Этот мысленный эксперимент использует как общую теорию относительности, так и принцип неопределённости квантовой механики. Обе теории предсказывают, что невозможно измерение с точностью, которая превосходит планковскую длину. Таким образом, в любой теории квантовой гравитации, комбинирующей общую теорию относительности и квантовую механику, традиционное представление о пространстве и времени неприменимо на расстояниях меньше планковской длины или для промежутков времени меньше чем планковское время.
Согласно теории струн, дополнительные 6 (или 7) измерений свёрнуты до размеров планковской длины и поэтому экспериментально не могут быть обнаружены.
Ссылки
См. также
| Другие результаты | |
| Сразу оговорюсь, что ваш контрольный список/торговый план не должен быть чересчур длинным или детализированным. | |
| Генеральный план Майка содержал удручающе длинный перечень проблем, которые необходимо было решить. | |
| Но на рассматриваемой странице есть более длинные слова без мягких дефисов, так что, интересно, Инг, каков план? | |
| Кроме длинных изогнутых наконечников, этот передний план имел прямые края и постоянную хорду; его размах составлял около 40% размаха основного самолета и менее 20% его площади. | |
План храма кандария Махадева имеет длину 109 футов на 60 футов и возвышается на 116 футов над землей и на 88 футов над собственным полом. | |
| Его план состоит из нефа, центральной башни, алтаря и северного придела, который тянется почти на всю длину церкви. | |
| Этот кусок ткани, достаточно узкий и длинный, вполне годился для осуществления ее плана. | |
| Самый длинный день претендовал на награду За лучшую операторскую работу, в то время как Пэтти Дюк была награждена лучшей актрисой второго плана за ее работу в Чудотворце. | |
| о длинных планах, снятых в одинаковой местности. | |
| Яма продолговатая в плане и имеет приблизительно 3,5 километра в длину, 1,5 километра в ширину и более 600 метров в глубину. | |
| Набережная прямая в плане и имеет длину около 310 метров. | |
| В своем плане церковь представляет собой крест с более короткими поперечными и более длинными продольными плечами. | |
В планерах контуры заземления также могут возникать из-за наличия только одного главного колеса вблизи центра тяжести, а также из-за того, что длинные крылья расположены близко к Земле. | |
| Рычаги от длинных крыльев могут оказывать большое давление на заднюю часть фюзеляжа, иногда ломая хвостовую балку, особенно на Т-образных планерах. | |
| Неблагоприятное рыскание более выражено для легких самолетов с длинными крыльями, таких как планеры. | |
| Самая большая планета Солнечной системы может передавать ток на расстояние своего диаметра и длины окружности. | |
| При этом мой хвост, когда полностью сформируется, будет длиннее, чем расстояние между планетами. | |
| Рано или поздно кометы с такой длинной эллиптической траекторией вокруг Солнца сталкиваются с планетами. | |
| Теоретически альбедо можно обнаружить и на непереходящих планетах, наблюдая вариации света с несколькими длинами волн. | |
А преимуществом этого небольшого социального дискомфорта является то, что когда дело касается бега в жару на длинные дистанции, мы великолепны, мы — самые лучшие на планете. | |
| Возможно год более длинен на этой планете. | |
| 3 метра в длину и впечатляющие 68 килограмм — вот размеры этих крупнейших ящериц на планете. | |
| Длинно травные равнины тропической Индии — дом крупнейших травоядных млекопитающих на нашей планете… и некоторых из наименьших. | |
| Мать совершила длинное путешествие, чтобы появится на этой планете. | |
| Рекорд по самому длинному расстоянию, пройденному транспортным средством на другой планете, в настоящее время принадлежит Луноходу Луноход-2. | |
| Если кто-нибудь это найдет,… я встретил замечательного нового друга… и он взял меня в длинное путешествие, чтобы показать его планету. | |
| Хотя это критическое значение исходящего длинноволнового излучения меньше предела Симпсона-Накадзимы, оно все еще оказывает драматическое воздействие на планету’ | |
Мы не только находим планеты, но и изучаем этот свет в волнах разной длины. | |
| Оно сдвинуло тектонические плиты Земли, ускорило вращение планеты и буквально сократило длину суток. | |
| Вулканы формируют опору самой длинной горной цепи нашей планеты — Анды в Южной Америке. | |
Является ли длина Планка наименьшей длиной, которая существует во вселенной, или это наименьшая длина, которую можно наблюдать?
Короткий ответ: никто не знает, но длина Планка в данном случае больше нумерологии, чем физики
Длинный ответ: Предположим, вы физик-теоретик. Ваша работа не связана с единицами, просто математика — вы никогда не используете тот факт, что с = 3 × 10 8 м / с с знак равно 3 × 10 8 м / s , но у вас, вероятно, есть с с всплывать в нескольких разных местах. Поскольку вы никогда не работаете с реальными физическими измерениями, вы решили работать в единицах с с = 1 с знак равно 1 , а затем вы поймете, когда вы доберетесь до конца уравнений, вы умножите на / делите на с с пока вы не получите правильные единицы. Итак, вы делаете относительность, вы пишете Е = м Е знак равно м и когда вы обнаружите, что скорость объекта равна .5, вы понимаете, что это должно быть .5 с 0,5 с и т. д. Вы понимаете, что с с в некотором смысле это «естественная шкала» для длин, времен, скоростей и т. д. Перемотка вперед, и вы начинаете замечать, что есть несколько таких констант, которые дают естественные масштабы для вселенной. Например, ℏ ℏ имеет тенденцию характеризовать, когда квантовые эффекты начинают иметь значение — часто люди говорят, что классический предел — это предел, где ℏ → 0 ℏ → 0 , хотя это может быть более тонким, чем это.
Итак, вы делаете относительность, вы пишете Е = м Е знак равно м и когда вы обнаружите, что скорость объекта равна .5, вы понимаете, что это должно быть .5 с 0,5 с и т. д. Вы понимаете, что с с в некотором смысле это «естественная шкала» для длин, времен, скоростей и т. д. Перемотка вперед, и вы начинаете замечать, что есть несколько таких констант, которые дают естественные масштабы для вселенной. Например, ℏ ℏ имеет тенденцию характеризовать, когда квантовые эффекты начинают иметь значение — часто люди говорят, что классический предел — это предел, где ℏ → 0 ℏ → 0 , хотя это может быть более тонким, чем это.
Итак, в любом случае, вы начинаете понимать, как построить фундаментальные единицы таким образом. Скорость света дает шкалу скорости, но как вы можете получить шкалу длины? Оказывается, вам нужно сжать его вместе с несколькими другими фундаментальными константами, и вы получите:
ℓ п = ℏ грамм с 3 — — — √ ℓ п знак равно ℏ грамм с 3
Я призываю вас решить это; у него есть единицы длины. Так что это круто! Может быть, это что-то важное? Это действительно маленький, в конце концов … ≈ 10 — 35 м ≈ 10 — 35 м , Может быть, это самая маленькая вещь!
Так что это круто! Может быть, это что-то важное? Это действительно маленький, в конце концов … ≈ 10 — 35 м ≈ 10 — 35 м , Может быть, это самая маленькая вещь!
Но давайте успокоимся на секунду. Что если я сделаю это для массы, чтобы найти «массу Планка»? Я получил:
м п = ℏ с грамм — — — √ ≈ 21 мкг м п знак равно ℏ с грамм ≈ 21 μ грамм
Хорошо, ну, микрограммы не огромны, но для физика элементарных частиц они огромны. Но вряд ли это какой-то фундаментальный предел чему-либо. Это не самая маленькая масса в мире. Википедия утверждает, что если бы масса заряженного объекта была такой большой, он разрушился бы, но заряженные точечные частицы даже близко не имеют этой массы, так что это не имеет значения.
Дело не в том, что эти вещи бессмысленны — они во многих случаях облегчают математику, и они говорят вам, как работать в подразделениях этих произвольных теоретиков. Но сейчас в эксперименте или в большинстве современных теорий нет веских оснований полагать, что это очень много значит, помимо предоставления шкалы.
Дэвид З ♦
Я бы оспорил, что никто не знает — я имею в виду, технически это правильно, но я бы сказал, что гипотеза о минимальной измеримой длине, по крайней мере, кажется несколько правдоподобной, тогда как гипотеза о минимальной длине, периоде, немного более «там» , Во всяком случае, очень хорошее объяснение.
WOJ
+1 — это очень интересное и занимательное объяснение, которое нужно дать ученикам / студентам, чтобы облегчить их контакты с физикой (говорит бывший физик)
corsiKa
«Предположим, что вы физик-теоретик», — звучит в точности так, как сказал бы физик-теоретик.
Андре
Происходит чуть больше, чем этот отличный ответ. Если мы используем свет, чтобы посмотреть на структуру объекта, нам нужно, чтобы его длина волны была предпочтительно меньше размера деталей, на которые мы хотим смотреть. Зондирование объекта, который имеет (линейный) размер, равный длине Планка, требует, чтобы энергия фотона была больше, чем масса черной дыры этого «размера». Итак, классическая черная дыра помешала бы нам видеть детали внутри этого объекта. Мы приводим к очевидному противоречию, которое предполагает несовместимость между Relativty и QM
Итак, классическая черная дыра помешала бы нам видеть детали внутри этого объекта. Мы приводим к очевидному противоречию, которое предполагает несовместимость между Relativty и QM
vhspdfg
В каком смысле «масштаб Планка выражает область, в которой предсказания Стандартной модели квантовой теории поля и общей теории относительности больше не совместимы»? Это то, что говорит Википедия, и на нее нет цитирования, хотя, похоже, об этом много говорится на многих страницах.
Мы все можем жить в бесконечной голограмме
NASA
Кварки и лептоны , строительные блоки материи, невероятно малы. Даже самые большие кварки имеют диаметр всего около аттометра (миллиардной миллиардной метра). Но увеличьте масштаб — в миллиард раз больше — мимо зептометров и йоктометров, туда, где у единиц закончились названия. Затем продолжайте движение, еще в сто миллионов раз меньше, и вы, наконец, достигнете дна: это длина Планка, приблизительно 1.6 x 10 -35 метров, по мнению физиков, самая короткая длина во Вселенной. По их словам, после этого само понятие расстояния теряет смысл.
Насколько малы мы говорим? Чтобы охватить песчинку, потребуется больше планковских длин, чем песчинок, чтобы охватить наблюдаемую Вселенную.
Тем не менее, идея ограничения конечного размера может показаться странной. В конце концов, если вы можете определить расстояние, вы можете просто сократить его вдвое — до бесконечности, верно? Не обязательно.Одно из величайших открытий 20-го века заключалось в том, что на малых масштабах многие физические свойства, такие как угловой момент и энергия, могут принимать только определенные дискретные значения, или «кванты». Этот принцип, подкрепленный десятилетиями экспериментов, является основой квантовой механики.
Это приводит к довольно важному вопросу: если свойства материи можно квантовать, как насчет самой ткани пространства-времени? Является ли Вселенная гладким континуумом, как это описано в теории относительности Эйнштейна? Или, если мы присмотримся очень близко, все это растворилось бы в мозаике мерцающих пикселей, как экран компьютера? Является ли реальность, которую мы наблюдаем, просто голограммой, состоящей из мельчайших точек?
Для исследования масштаба Планка с помощью ускорителя частиц потребуется инструмент размером с нашу галактику.Но у ученых из Фермилаба, недалеко от Чикаго, есть удивительно скромное новое устройство под названием Холометр, которое может дать некоторые подсказки. Используя пару твердотельных лазеров и несколько точно отполированных зеркал, они надеются уловить явное дрожание этих гипотетических пикселей — так называемый «голографический шум» после нечеткости голограмм. Если они его найдут? Добро пожаловать в Матрицу.
Планковская длина
Планковская длина
Следующая: Топологическая квантовая теория поля
Вверх: Планка
Предыдущая: Введение
В общей теории относительности присутствуют две константы: скорость света.
и гравитационная постоянная Ньютона.Этого не должно быть
сюрприз, поскольку Эйнштейн создал общую теорию относительности, чтобы согласовать
успех теории гравитации Ньютона, основанной на мгновенном действии на
дистанции, с его новой специальной теорией относительности, в которой нет
влияние распространяется быстрее света. Константа также появляется в
квантовая теория поля, но в паре с другим партнером: Планковский
постоянный . Причина в том, что квантовая теория поля принимает
учитывать специальную теорию относительности и квантовую теорию, в которой
устанавливает масштаб, при котором принцип неопределенности становится важным.
Разумно подозревать, что любая теория, согласующаяся с общим мнением
теория относительности и квантовая теория будут включать все три константы,,
а также . Планк отметил, что помимо числовых факторов
это уникальный способ использовать эти константы для определения единиц длины, времени,
и масса. Например, теперь мы можем определить единицу длины
называется «длина Планка» следующим образом:
Это крайне мало: около
метров. Физики
давно подозревали, что квантовая гравитация станет важной для
понимание физики примерно в этом масштабе.Причина очень проста: любой
расчет, который предсказывает длину, используя только константы, и
должен дать длину Планка, возможно, умноженную на
неважный числовой коэффициент вроде.
Например, квантовая теория поля утверждает, что с любой массой
существует длина, называемая ее комптоновской длиной волны, такая, что
определение положения частицы массы с точностью до одного комптона
длина волны требует достаточно энергии, чтобы создать еще одну частицу этого
масса. Создание частиц — это типично квантово-теоретико-полевой
явление.Таким образом, мы можем сказать, что длина волны Комптона задает
шкала расстояний, на которой квантовая теория поля становится решающей для
понимание поведения частицы данной массы. С другой
стороны, общая теория относительности утверждает, что с любой массой связана
длина, называемая радиусом Шварцшильда, такая, что сжатие
объект массы до размера меньше, чем это приводит к
образование черной дыры. Радиус Шварцшильда примерно равен
шкала расстояний, на которой общая теория относительности становится решающей для
понимание поведения объекта данной массы.Теперь, игнорируя
некоторые числовые факторы, мы имеем
а также
Эти две длины становятся равными, когда масса Планка. А также
когда это происходит, они оба равны планковской длине!
Таким образом, по крайней мере наивно, мы ожидаем, что как общая теория относительности, так и
квантовая теория поля потребуется, чтобы понять поведение
объект, масса которого примерно равна массе Планка, а радиус — примерно
Планковская длина. Это не только объясняет некоторую важность
Планковский масштаб, но и некоторые трудности в получении
экспериментальные данные о физике в этом масштабе.Большинство наших
информация об общей теории относительности поступает из наблюдения тяжелых объектов
как планеты и звезды, для которых
. Большинство наших
информация о квантовой теории поля поступает из наблюдения за светом
такие объекты, как электроны и протоны, для которых
. В
Масса Планка занимает промежуточное положение между ними: около массы огромного
клетка. Но длина Планка примерно в разы
радиус протона! Изучить ситуацию, когда как общие
теория относительности и квантовая теория поля важны, мы могли бы попытаться
сжать клетку до размера, в несколько раз превышающего размер протона.Мы
не знаю причин, по которым это невозможно в принципе. Но мы понятия не имеем
как на самом деле совершить такой подвиг.
В приведенном выше аргументе есть несколько хорошо известных лазеек. В
«неважный числовой фактор», о котором я упоминал выше, на самом деле может быть очень
большой или очень маленький. Теория квантовой гравитации может сделать
предсказания безразмерных величин, таких как соотношение мюона и
массы электронов. В этом отношении теория квантовой гравитации могла бы
включают физические константы, отличные от, и.В
последние две альтернативы особенно правдоподобны, если мы изучаем квантовую
гравитация как часть более крупной теории, описывающей другие силы и
частицы. Однако, хотя мы не можем доказать, что длина Планка
имеет важное значение для квантовой гравитации, я думаю, мы можем почерпнуть некоторую мудрость
от размышлений о константах и - и многом другом
важно то, что физическое понимание, которое заставляет нас рассматривать эти
константы не менее важны.
В чем важность константы? В специальной теории относительности
важно появление этой константы в Минковском
метрика
который определяет геометрию пространства-времени и, в частности, световой конус
через каждую точку.Отступая от конкретного формализма, мы
можно увидеть несколько идей в действии. Во-первых, пространство и время образуют единое целое.
целое, которое можно представить себе геометрически. Во-вторых, количества
значения которых мы стремимся предсказать, локализованы. То есть мы можем измерить
их в небольших областях пространства-времени (иногда идеализируемых как точки).
Физики называют такие величины «локальными степенями свободы». И в-третьих,
чтобы предсказать значение величины, которая может быть измерена в каком-либо регионе
, нам нужно использовать только значения величин, измеренных в регионах,
стоять в определенном геометрическом отношении к.Это отношение называется
«причинная структура» пространства-времени. Например, в релятивистском
теория поля, чтобы предсказать значение полей в некоторой области, она
достаточно использовать их значения в любой другой области, которая пересекает каждую
времяподобный путь, проходящий. Обычный способ резюмировать это
идея состоит в том, чтобы сказать, что ничто не движется быстрее света. Я предпочитаю говорить
что хорошая физическая теория должна иметь локальную степень свободы
каузальное распространение .
В ньютоновской гравитации это просто сила гравитационного
поле.Это приобретает более глубокое значение в общей теории относительности, где
гравитационное поле описывается в терминах кривизны
метрика пространства-времени. В отличие от специальной теории относительности, где Минковский
метрика — это «фоновая структура», заданная априори в ОТО.
метрика рассматривается как поле, которое не только влияет, но и
затронуты, присутствуют другие поля. Другими словами, геометрия
пространство-время становится локальной степенью свободы теории.
Количественно взаимодействие метрического и других полей
описывается уравнением Эйнштейна
где тензор Эйнштейна зависит от кривизны
метрической, а тензор энергии-импульса описывает поток
энергии и импульса за счет всех других полей.Роль
константа, таким образом, просто для количественной оценки того, насколько геометрия
на пространство-время влияют другие поля. За долгие годы у людей
понял, что великий урок общей теории относительности состоит в том, что
теория физики не должна содержать геометрических структур, влияющих на
локальные степени свободы, оставаясь при этом незатронутыми ими. Вместо,
все геометрические структуры — и в частности причинная структура —
сами должны быть локальными степенями свободы. Короче говоря,
что теория должна быть без фона .
Борьба за освобождение от фоновых структур началась давно.
до того, как Эйнштейн разработал общую теорию относительности, и все еще не завершен.
Конфликт между космологиями Птолемея и Коперника, диспут
между Ньютоном и Лейбницем относительно абсолютного и относительного движения, и
современные аргументы относительно «проблемы времени» в квантовой гравитации
— все это лишь главы в истории этой борьбы. у меня нет
место для наброска этой истории здесь, и даже для того, чтобы уточнить ее
важнейшее понятие «геометрическая структура».Я могу только указать на
читатель к литературе, начиная, пожалуй, с книг
Барбур [9] и Эрман [15], различные статьи автора
Ровелли [25,26,27] и многочисленные ссылки в нем.
Наконец, что из? В квантовой теории это кажется наиболее вероятным.
заметно в коммутационном соотношении между импульсом и
положение частицы:
вместе с аналогичными коммутационными соотношениями с участием других пар
измеримые величины. Потому что наша способность измерять две величины
одновременно с полной точностью ограничена их неспособностью
добираться до работы, количественно оценивает нашу неспособность одновременно знать
все, что можно знать о мире.Но это далеко
больше к квантовой теории, чем к принципу неопределенности. На практике,
приходит вместе со всем формализмом комплексных гильбертовых пространств
и линейные операторы.
Существует широко распространенное мнение, что принципы, лежащие в основе квантовой теории
плохо изучены по сравнению с общей теорией относительности. Это
привели к многочисленным дискуссиям по вопросам интерпретации. Однако я делаю
не думайте, что квантовая теория потеряет свою тайну из-за таких
обсуждения. Я считаю, что настоящая проблема — лучше понять, почему
математический формализм квантовой теории — это как раз то, что есть.Исследования в области квантовой логики проделали прекрасную работу по пониманию
область кандидатов, из которой был взят конкретный формализм, который мы используем.
выбрал. Но что же такого особенного в этом выборе?
Почему, например, мы используем комплексные гильбертовы пространства, а не действительные или
кватернионные? Это решение принято исключительно для установки экспериментального
данные, или есть более глубокая причина? Поскольку подобных вопросов пока нет
есть четкие ответы, я резюмирую физическое понимание, лежащее в основе
просто сказав, что хорошая теория физической вселенной
должна быть квантовая теория — оставляя открытой возможность
в конце концов сказал что-то более разъясняющее.
Попытавшись извлечь идеи, лежащие в основе констант
и мы лучше понимаем задачу
построение теории квантовой гравитации. Общая теория относительности
признает важность и идеализирует реальность,
рассматривать как ничтожно малые. Из нашего обсуждения выше мы видим
что это потому, что общая теория относительности не имеет фона
классическая теория с причинно распространяющимися локальными степенями свободы.
С другой стороны, обычная квантовая теория поля
признает, но рассматривает как незначительное, потому что это
квантовая теория, зависящая от фона, с локальными степенями свободы
распространяется причинно.
Самый консервативный подход к квантовой гравитации — это поиск теории
который сочетает в себе лучшие черты общей теории относительности и квантового поля
теория. Для этого надо попробовать найти без фона.
квантовая теория с причинно распространяющимися локальными степенями свободы .
Хотя этот подход может не принести успеха, его определенно стоит использовать.
Учитывая отсутствие экспериментальных доказательств, которые указали бы нам на
принципиально новые принципы, мы должны постараться понять
Полное применение принципов, которые у нас уже есть!
Из моего описания цели, возможно, можно увидеть некоторые из
трудности.Поскольку квантовая гравитация должна быть свободной от фона,
геометрические структуры, определяющие причинную структуру пространства-времени, должны
сами по себе являются локальными степенями свободы, распространяющимися причинно. Этого достаточно
уже верно в общей теории относительности. Но поскольку квантовая гравитация
должна быть квантовой теорией, эти степени свободы следует рассматривать
квантово-механически. Так что, по крайней мере, мы должны разработать квантовую
теория некой геометрической структуры, которая может определять причинно-следственные связи.
структура в пространстве-времени.
Теория струн не продвинулась далеко в этом направлении. Эта теория
обычно формулируется с помощью метрики пространства-времени, которая
рассматривается как фоновая структура, а не как локальная степень свободы
как и остальные. Большинство теоретиков струн признают, что это
неудовлетворительная ситуация, и к настоящему времени многие борются за
бесфоновая формулировка теории. Однако, по словам
два эксперта [18], «кажется, что еще более радикальный отход
из традиционных представлений о пространстве и времени может потребоваться
прийти к действительно независимой от фона формулировке.»
Петлевая квантовая гравитация прошла долгий путь к развитию
безфоновая квантовая теория геометрии пространства
[1,28], но не так уж и далеко, когда дело касается пространства-времени.
Это затруднило понимание динамики, в частности
причинное распространение степеней свободы. Работайте над этими
выпусков началось совсем недавно. Одна из причин для оптимизма — недавний
успех в понимании квантовой гравитации в трех измерениях пространства-времени.
Но чтобы объяснить это, я должен сначала сказать немного о топологической квантовой
теория поля.
Далее: Топологическая квантовая теория поля
Вверх: Планка
Предыдущая: Введение
© 1999 Джон Баез
[email protected]
дом
Планковское время
Планковское время
Планковское время :
Характерный линейный размер задается как определенная комбинация
три самые фундаментальные константы природы: (1) постоянная Планка h
(назван в честь немецкого физика Макса Планка, основателя квантовой теории
физика), (2) скорость света c и (3) универсальная гравитационная
постоянная G.Комбинация, называемая длиной Планка (Gh / c 3 ) 1/2 ,
равняется примерно 10 -33 см, что намного меньше, чем расстояния, на которые
элементарные частицы можно исследовать в ускорителях частиц на Земле.
Энергии, необходимые для того, чтобы разбить частицы до планковской длины каждой
другие были доступны Вселенной в то время, которое равнялось планковской длине
делится на скорость света. На этот раз, названный временем Планка
(Gh / c 5 ) 1/2 , приблизительно равно 10 -43 секунд.На
Планковское время считается, что массовая плотность Вселенной приближается к
Планковская плотность, c 5 / чG 2 , примерно 10 93 г / куб. Содержится в
Планковский объем — это масса Планка (hc / G) 1/2 , примерно
10 -5 г. Объект такой массы был бы квантовой черной дырой,
с горизонтом событий, близким к его собственной комптоновской длине (расстояние более
частица квантово-механически «нечеткая») и размер
космический горизонт в планковское время.В таких экстремальных условиях
пространство-время нельзя рассматривать как классический континуум, и ему нужно дать
квантовая интерпретация.
Последнее является целью теории супергравитации, одной из
имеет любопытное представление о том, что четыре измерения пространства-времени (три
пространственные измерения плюс одно временное измерение) знакомого мира может быть
иллюзия. Реальное пространство-время, в соответствии с этой картинкой, имеет 26 или 10
измерения пространства-времени, но все эти измерения, кроме обычных четырех
каким-то образом уплотнены или скручены до размеров, сопоставимых с планковскими
шкала.Так ускользнуло существование этих других измерений
обнаружение. Предположительно это произошло только в эпоху Планка, когда обычное
четыре измерения пространства-времени приобретают свои естественные планковские масштабы, что
существование чего-то более фундаментального, чем обычные идеи массы-энергии
и пространство-время раскрывается полностью. К сожалению, попытки вывести
что-либо более количественное или физически разъясняющее из теории имеет
увяз в неразрешимой математике этого сложного предмета. В
В настоящее время теория суперструн остается скорее загадкой, чем
решение.{1/2} $ — это единственное произведение степеней $ \ hbar, G, c $, трех наиболее универсальных размерных констант, имеющее единицу длины. Поскольку константы $ \ hbar, G, c $ описывают фундаментальные процессы квантовой механики, гравитации и специальной теории относительности, соответственно, полученный таким образом масштаб длины выражает типичный масштаб длины процессов, зависящих от релятивистской квантовой гравитации. 2 $ i.{-1/2} $ того же объекта, с точностью до числовых коэффициентов, таких как $ 2 $ и $ \ pi $. Время, необходимое для испарения такой черной дыры излучением Хокинга, также равно планковскому времени, то есть планковской длине, деленной на скорость света. Меньшие (более легкие) черные дыры вообще не ведут себя как черные дыры; они являются элементарными частицами (и время жизни короче планковского времени — признак того, что вы не можете доверять общей теории относительности для таких сверхкрохотных объектов). Черные дыры большего размера, чем длина Планка, все чаще ведут себя как долгоживущие черные дыры, известные нам из астрофизики.2 $ из-за квантовых флуктуаций метрического тензора; поправки к действию Эйнштейна-Гильберта с высшими производными; нелокальные явления и т. д.
Необычные поправки к геометрии, включая нелокальные явления, становятся настолько сильными на расстояниях, которые формально короче планковской длины, что нет смысла рассматривать какие-либо более короткие расстояния. Обычные правила геометрии там нарушатся. Планковская длина или около того также является самой короткой шкалой расстояний, которую могут исследовать ускорители, даже в принципе.Если бы кто-то увеличивал энергию протонов на LHC и выбрал коллайдер с радиусом, сопоставимым с Вселенной, длина волны протонов стала бы короче обратно пропорционально энергии протонов. Однако, как только энергия центра масс протонов достигает планковского масштаба, начинается образование «минимальных черных дыр», упомянутых выше. Последующее увеличение энергии приведет к появлению более крупных черных дыр с худшим, а не лучшим разрешением. Таким образом, планковская длина — это минимальное расстояние, которое можно исследовать.
Важно отметить, что мы говорим о внутренней архитектуре частиц и объектов. Многие другие величины, имеющие единицы длины, могут быть намного короче планковской длины. Например, длина волны фотона, очевидно, может быть произвольно короткой: любой фотон всегда можно усилить, как гарантирует специальная теория относительности, так что его длина волны станет еще короче.
О физике планковской шкалы известно многое (идеи из тысяч статей некоторых из лучших физиков мира), особенно некоторые ее качественные особенности, независимо от экспериментальной недоступности этой области.
Планковское время — EWT
Пояснение
Планковское время — еще одна фундаментальная физическая константа, названная в честь Макса Планка. В разделе о пространстве-времени единицы Планка описаны как компоненты самого пространства-времени, называемые гранулами , которые можно классически моделировать как систему пружина-масса для получения фундаментальных физических констант, где требуются только пять фундаментальных констант. На следующем рисунке показано соотношение четырех из этих постоянных Планка.
Элементарная ячейка пространственно-временной решетки
Планковское время — это фундаментальная классическая постоянная, устанавливающая базовую линию для единицы времени. Это время, за которое свет проходит расстояние в одну планковскую длину.
Планковское время — время, необходимое свету для прохождения планковской длины
См. Также: Планковская длина, Планковская масса, Планковский заряд
Деривация — Планковское время
В классическом формате констант время Планка является одной из пяти фундаментальных физических констант, из которых можно вывести большинство других констант.Здесь установлена скорость света (c), которая не является одной из пяти фундаментальных констант, чтобы установить ее значение. Это время, за которое волна распространяется на расстояние радиуса гранулы — планковскую длину.
В формате волновой постоянной это комплексное отношение квадрата длины волны, деленного на амплитуду и свойство электрона, и скорость света.
Расчетное значение: 5,3912E-44
Отличие от CODATA: 0.000%
Расчетные единицы : с (время в секундах)
G-фактор: г λ 2
Его значение было рассчитано и соответствует известному значению в таблице сводных расчетов. Вывод этой константы доступен в статье «Основные физические константы».
Что такое шкала Планка и почему физики ее используют?
Какое значение имеют планковское время, планковская длина и планковская масса? изначально появился на Quora- , где можно получить и поделиться знаниями, давая людям возможность учиться у других и лучше понимать мир.
Ответ от Фрэнк Хейл, доктор философии. Физика, Стэнфордский университет, на Quora:
В физике много констант. Например, масса электрона, заряд электрона, отношение массы электрона к массе протона, длина волны света, излучаемого определенным атомным переходом и т. Д. Но все это константы так или иначе связаны с определенными видами объектов в нашей вселенной — они не применимы ко всему во вселенной, поэтому они не являются действительно фундаментальными.
На самом деле существует всего несколько фундаментальных констант , которые имеют единицы измерения, которые можно объединить в единицу длины, времени или энергии. Опять же, под фундаментальными я имею в виду константы, которые так или иначе применимы ко всей вселенной. Фактически, единственными известными действительно фундаментальными константами являются:
- c — скорость света. Это не просто скорость света, это действительно коэффициент преобразования между измерением времени и тремя измерениями пространства в нашем 4-х мерном пространстве-времени.2): гравитационная постоянная
Есть еще одна константа, которая кажется фундаментальной: постоянная Больцмана (постоянная Больцмана). Эта константа имеет единицы энергии / градус Кельвина, и поэтому постоянная Больцмана на самом деле является просто определением 1 градуса Кельвина. Таким образом, постоянная Больцмана на самом деле не является фундаментальной константой, которая что-то говорит нам о Вселенной.
Итак, вот и все, нет других фундаментальных констант, применимых ко всей вселенной и всему ее содержимому.
Теперь из этих трех фундаментальных констант мы можем построить шкалы длины, времени и энергии следующим образом:
Итак, «по сути», шкала Планка — единственная шкала, которая применима ко всему во Вселенной. Следовательно, эти единицы являются наиболее естественными для измерения расстояния, времени, энергии и массы. Фактически, физики-теоретики часто работают в системе единиц, где c = 1, ħ = 1 и G = 1 — из формул выше вы можете видеть, что единицы, которые они используют в этом случае, равны , ровно по шкале Планка. единиц, начиная с , все единицы Планка будут иметь числовое значение « 1 », если c = 1, 8 = 1 и G = 1!
С точки зрения значимости Планковского масштаба:
- Считается, что это шкала струн теории струн.Таким образом, струны имеют длину примерно равную планковской длине и колеблются на планковских временных масштабах.
- Если энергия Планка ограничена объемом куба размером 1 планковская длина, он образует черную дыру. Фактически, это считается наименьшей возможной массой для черной дыры, и на этих «планковских» расстояниях, временах и энергиях считается, что квантовые гравитационные эффекты будут очень значительными.
- Планковская длина — это наименьшая шкала расстояний, которую мы можем исследовать с помощью ускорителей.Ускорители высоких энергий используются для исследования небольших объектов, таких как кварки внутри протонов, поэтому цель всегда заключается в создании ускорителей более высоких энергий. Однако, если бы мы могли построить ускоритель, который достигал бы энергии Планка для частицы, такой как электрон, когда электрон взаимодействовал бы с целью, образовалась бы черная дыра, и это не помогло бы перейти к более высоким энергиям, чем эта, поскольку черная дыра будет просто стань больше. Вот почему планковская длина — это наименьший масштаб длины, который мы могли бы теоретически исследовать.
- Планковское время — это время, за которое свет проходит планковскую длину.
- Считается, что примерно в планковское время после Большого взрыва гравитация отделится от трех других сил природы (сильной, слабой и электромагнитной).
Есть много предположений о других вещах, которые могут произойти в масштабе Планка. Например,
- Пространство-время может превратиться в хаотическую квантовую пену из-за гравитационных флуктуаций из-за квантовых флуктуаций такого масштаба.
- Пространство-время может квантоваться (что вызовет нарушения лоренц-инвариантности в масштабе Планка.
Но, повторяю, это предположения — мы действительно не знаем, что происходит в масштабе Планка.
Одно интересное замечание: планковская длина и планковское время на много порядков меньше, чем длины или времена, которые мы можем измерить. Энергия макроскопических объектов намного превышает планковскую. Однако, если вы разделите энергию макроскопического тела на количество частиц в теле, энергия, приходящаяся на одну частицу, будет на много порядков меньше энергии Планка.20 эВ, что на 8 порядков ниже энергии Планка (см. Частицу Oh-My-God). Этот космический луч с самой высокой энергией действительно имел кинетическую энергию, равную кинетической энергии бейсбольного мяча весом 5 унций (142 г), летящего со скоростью около 100 километров в час (60 миль в час). Чтобы получить энергию Планка, рассмотрим химическую энергию, хранящуюся в автомобильном бензобаке (57,2 л бензина при 34,2 МДж / л) — это примерно энергия Планка. Таким образом, энергия Планка может проехать на вашем автомобиле несколько сотен миль или километров!
Планковская масса составляет примерно 1% от массы типичного комара (см. Планковую массу — Вольфрам | Альфа), поэтому энергия этого бака с бензином эквивалентна 1% массы комара, преобразуемой в энергию! Основная причина того, почему масса Планка такая большая, заключается в том, что гравитационная сила в этой Вселенной очень мала.Масса Планки, ограниченная объемом Планка, будет черной дырой, и поскольку гравитация настолько мала, требуется большое количество массы, чтобы гравитация была достаточно сильной, чтобы сформировать черную дыру в этом объеме.
Этот вопрос первоначально появился на Quora — месте, где можно получить и поделиться знаниями, давая людям возможность учиться у других и лучше понимать мир. Вы можете подписаться на Quora в Twitter, Facebook и Google+. Еще вопросы:
Вызов всех фанатов HuffPost!
Подпишитесь на членство, чтобы стать одним из основателей и помочь сформировать следующую главу HuffPost
Есть ли у природы минимальная длина?
Молекулы состоят из атомов.Атомные ядра состоят из нейтронов и протонов. А нейтроны и протоны состоят из кварков и глюонов. Многие физики думают, что это не конец истории, но что кварки и глюоны состоят из еще более мелких вещей, например крошечных вибрирующих струн, о которых и идет речь в теории струн. Но что потом? Струны снова сделаны из более мелких вещей? Или существует наименьший масштаб, за пределами которого природа просто не имеет дальнейшей структуры? У природы минимальная длина?
Об этом мы и поговорим сегодня.
Когда физики говорят о минимальной длине, обычно имеют в виду планковскую длину, которая составляет примерно 10 -35 метров. Планковская длина названа в честь Макса Планка, который представил ее в 1899 году. 10 -35 метров звучит крошечным, и действительно, чертовски крошечным.
Чтобы дать вам представление, представьте себе туннель Большого адронного коллайдера. Это кольцо диаметром около 10 километров. Планковская длина сравнивается с диаметром протона, как радиус протона с диаметром Большого адронного коллайдера.
В настоящее время самые маленькие структуры, которые мы можем изучить, имеют размер от десяти до минус девятнадцати метров. Это то, что мы можем сделать с энергией, производимой на Большом адронном коллайдере, которая все еще на шестнадцать порядков больше планковской длины.
Что такого особенного в длине Планка? Кажется, что планковская длина устанавливает предел того, насколько маленькой может быть структура, чтобы мы могли ее измерить. Это потому, что для измерения небольших конструкций нам нужно сжать больше энергии в небольших объемах пространства.В основном это то, что мы делаем с ускорителями элементарных частиц. Более высокая энергия позволяет нам узнать, что происходит на более коротких расстояниях. Но если вы вложите слишком много энергии в небольшой объем, вы получите черную дыру.
Более конкретно, если у вас есть энергия E , это в лучшем случае позволит вам разрешить расстояние примерно ℏ c / E . Я назову это расстояние Δ x . Здесь c — скорость света, а ℏ — естественная постоянная, называемая постоянной Планка.Да, это тот же Планк! Это соотношение исходит из принципа неопределенности квантовой механики. Таким образом, более высокие энергии позволяют разрешать более мелкие структуры.
Теперь вы можете спросить, если я увеличу энергию и размер, который я могу разрешить, станет меньше, когда я получу черную дыру? Это хорошо, если радиус Шварцшильда, связанный с энергией, подобен расстоянию, которое вы пытаетесь измерить. Подсчитать это несложно. Так что давай сделаем это.
Радиус Шварцшильда составляет примерно M умножить на G / c 2 , где G — постоянная Ньютона, а M — масса.Мы спрашиваем, когда этот радиус аналогичен расстоянию Δ x . Как вы почти наверняка знаете, масса, связанная с энергией, равна E = Mc 2 . И, как мы уже видели, эта энергия составляет всего ℏ c / Δ x . Затем вы можете решить это уравнение для Δ x . И это то, что мы называем длиной Планка. Это связано с энергией, называемой энергией Планка. Если вы перейдете к более высоким энергиям, вы просто создадите большие черные дыры.Таким образом, длина Планка — это кратчайшее расстояние, которое вы можете измерить.
Итак, это точная оценка, и она не совсем неверна, но это не точный вывод. Если вы начнете думать об этом, это немного сложно, поэтому позвольте мне заверить вас, что есть гораздо более строгие способы сделать этот расчет, и вывод остается в основном тем же. Если объединить квантовую механику с гравитацией, то кажется, что длина Планка ограничит разрешение структур. Вот почему физики считают, что природа может иметь принципиально минимальную длину.
Макс Планк, кстати, не придумал планковскую длину, потому что считал ее минимальной. Он придумал это просто потому, что это единственная единица измерения длины, которую вы можете создать из фундаментальных констант, c, скорости света, G , постоянной Ньютона и ℏ. Он подумал, что это интересно, потому что, как он писал в своей статье 1899 года, это будут естественные единицы, которые также будут использовать инопланетяне.
Идея о том, что планковская длина является минимальной длиной, возникла только после развития общей теории относительности, когда физики начали думать о том, как квантовать гравитацию.Сегодня эта идея подтверждается попытками разработать теорию квантовой гравитации, о которой я рассказывал вам в более раннем видео.
В теории струн, например, если вы вложите в струну слишком много энергии, она начнет распространяться. В петлевой квантовой гравитации петли сами по себе имеют конечный размер, определяемый длиной Планка. В асимптотически безопасной гравитации сила тяжести становится слабее при высоких энергиях, поэтому после определенного момента вы больше не можете улучшить свое разрешение.
Когда я говорю о минимальной длине, многие люди, кажется, имеют в виду определенное изображение, а именно, что минимальная длина работает как своего рода дискретизация, пикселизация фотографии или что-то в этом роде.Но это определенно неправильный образ. Минимальная длина, о которой мы здесь говорим, больше похожа на неизбежное размытие изображения, некую фундаментальную размытость, присущую природе. Это может быть, но не обязательно, с дискретизацией.
Что все это значит? Что ж, это означает, что мы могли бы быть близки к созданию окончательной теории, которая описывает природу на ее самом фундаментальном уровне, и больше ничего нет. Это возможно, но. Помните, что аргументы в пользу существования минимальной длины основываются на экстраполяции на 16 порядков ниже расстояний, которые мы тестировали до сих пор.Это много. Эта экстраполяция может быть ошибочной. Несмотря на то, что в настоящее время у нас нет никаких оснований полагать, что должно быть что-то новое на расстояниях даже короче планковской длины, эта ситуация может измениться в будущем.
Тем не менее, я нахожу интригующим то, что из всего, что мы в настоящее время знаем, нет необходимости думать о расстояниях, меньших, чем длина Планка.
.

 Чистое число, которое мы называем постоянной тонкой структуры и обозначаем α, представляет собой комбинацию заряда электрона e , скорости света c и постоянной Планка h . Сначала у нас может возникнуть соблазн подумать, что мир, в котором скорость света меньше, будет другим миром. Но это было бы ошибкой. Если бы все c , h и e были изменены так, чтобы их значения в метрических (или любых других) единицах были другими, когда мы искали их в наших таблицах физических констант, но значение α осталось прежним, этот новый мир было бы неотличимо от нашего мира с точки зрения наблюдения . Единственное, что имеет значение при определении миров, — это значения безразмерных констант Природы. Если бы все массы были удвоены по величине [включая массу Планка m P ], вы не можете сказать, потому что все чистые числа, определяемые отношениями любой пары масс, не изменились.
Чистое число, которое мы называем постоянной тонкой структуры и обозначаем α, представляет собой комбинацию заряда электрона e , скорости света c и постоянной Планка h . Сначала у нас может возникнуть соблазн подумать, что мир, в котором скорость света меньше, будет другим миром. Но это было бы ошибкой. Если бы все c , h и e были изменены так, чтобы их значения в метрических (или любых других) единицах были другими, когда мы искали их в наших таблицах физических констант, но значение α осталось прежним, этот новый мир было бы неотличимо от нашего мира с точки зрения наблюдения . Единственное, что имеет значение при определении миров, — это значения безразмерных констант Природы. Если бы все массы были удвоены по величине [включая массу Планка m P ], вы не можете сказать, потому что все чистые числа, определяемые отношениями любой пары масс, не изменились.

 С. 287–296. Архивировано из оригинального (PDF) 17 июня 2006 года.
С. 287–296. Архивировано из оригинального (PDF) 17 июня 2006 года.