Измерение углов. Транспортир. Виды углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Измерение углов. Транспортир. Виды углов
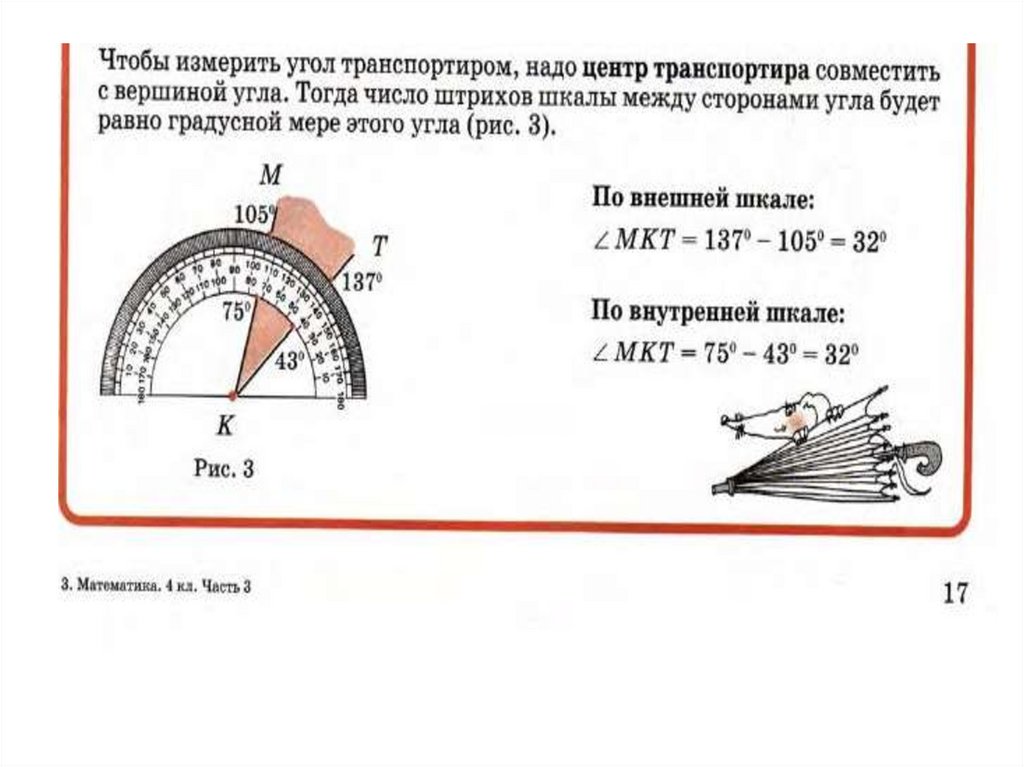
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1°.
Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .
Говорят: «Угол ABC равен 120 градусам». Пишут: .
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеет меньшую градусную меру.
- Развернутый угол равен .
- Неразвернутый угол меньше .
- Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже
АОС = АОВ + ВОС.
Виды углов:
- Острый угол — угол, градусная мера которого меньше 90°.
- Прямой угол — угол, градусная мера которого равна 90°.
- Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

- Развернутый угол — угол, градусная мера которого равна 180°.
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 900.
АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 900.
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1662,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1666,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1771,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1777,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 303,
Мерзляк, Полонский, Якир, Учебник
Номер 309,
Мерзляк, Полонский, Якир, Учебник
Номер 354,
Мерзляк, Полонский, Якир, Учебник
Номер 500,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 14,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 392,
Мерзляк, Полонский, Якир, Учебник
Номер 433,
Мерзляк, Полонский, Якир, Учебник
Номер 687,
Мерзляк, Полонский, Якир, Учебник
Номер 1235,
Мерзляк, Полонский, Якир, Учебник
Номер 1283,
Мерзляк, Полонский, Якир, Учебник
Задание 163,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1385,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1425,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1571,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759,
Мерзляк, Полонский, Якир, Учебник
Как измерять острые углы транспортиром.
 Конспект урока по математике на тему: «Транспортир
Конспект урока по математике на тему: «Транспортир
Измерить угол
— значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус
— это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор — транспортир
:
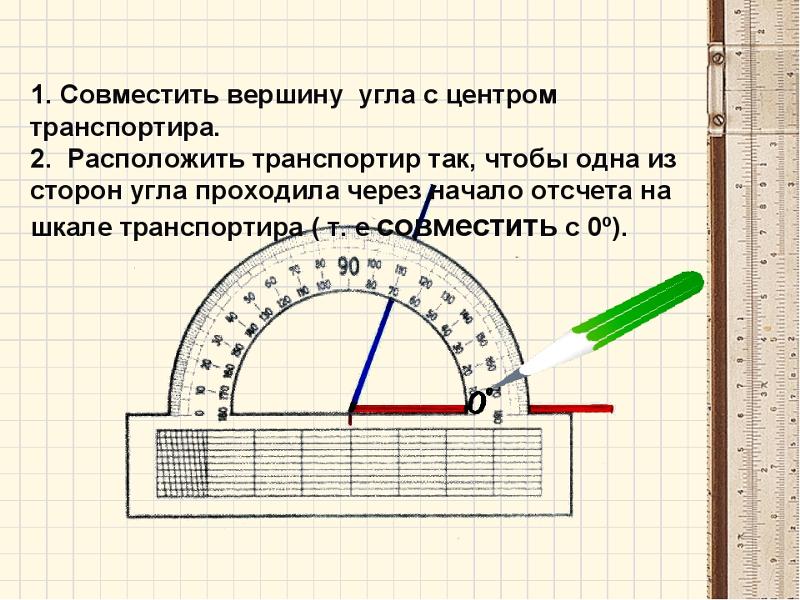
У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC
равен 60 градусов, угол MON
равен 120 градусов и пишут: ∠BOC
= 60°, ∠MON
= 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута
— это угол, равный
части градуса. Секунда
— это угол, равный части минуты. Минуты обозначают знаком »
, a секунды — знаком «»
. Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34»
19«»
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB
:
Луч OD
делит его на два угла: ∠AOD
и ∠DOB
. Таким образом, ∠AOB
= ∠AOD
+ ∠DOB
.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Каждый школьник знает, что такое транспортир. Этот, казалось бы, неприглядный инструмент выполняет очень важные функции не только на уроках математики. О том,что он собой представляет, а также как правильно им пользоваться, расскажем далее.
Что такое транспортир?
Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.
Правила пользования
В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.
Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.
Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.
Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.
Измеряем угол
Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:
- Острый. Таким называют угол до 90 градусов.
- Прямым является угол, равный 90 градусам.
- варьируется в диапазоне от 90 до 180 градусов.
- представляет собой прямую линию или 180 градусов.
- Полный угол выглядит как окружность и составляет 360 градусов.
Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.
Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.
Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.
Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.
Набор школьника
Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее.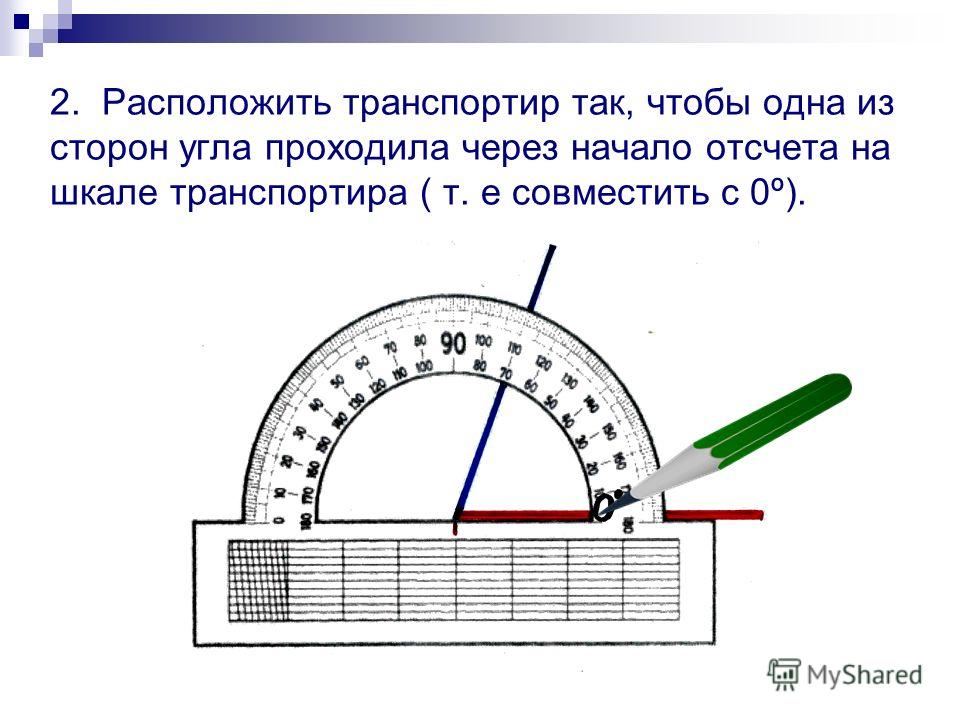 Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой
Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой
Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей. Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.
Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.
Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.
В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.
Итог
Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!
§ 1 В чем измеряют углы?
С древнейших времен люди сталкивались с необходимостью измерять. Измерения нужны повсеместно: в строительстве, медицине, на производстве, да где угодно! Например, расстояния измеряют в метрах или километрах, массу мы меряем килограммами, тоннами, граммами, а в чем измеряют углы? Оказывается, углы измеряются в градусах! Понятие градуса и появление первых инструментов для измерения углов исторически принято связывать с развитием цивилизации в древнем Вавилоне, хотя само слово градус имеет латинское происхождение (градус — от лат. gradus «шаг, ступень»).
gradus «шаг, ступень»).
Как вы думаете, есть ли величина измерения углов меньшая градуса? Оказывается, существуют такие единицы измерения, как минута (это одна шестидесятая часть градуса) и секунда (это одна шестидесятая часть минуты). Названия «минута» и «секунда», также произошли от латинских слов, и в переводе означают «части меньшие первые» и «части меньшие вторые». В истории науки эти единицы измерения сохранились благодаря Клавдию Птолемею, жившему во II веке.
§ 2 Транспортир. Построение углов транспортиром
Единицами измерения углов являются градусы, а чем же можно измерять углы? Для измерения углов применяют транспортир. Шкала транспортира располагается на полуокружности. Центр этой полуокружности отмечен на транспортире черточкой. Штрихи шкалы транспортира делят полуокружность на 180 долей. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен доле развернутого угла. Такие углы и называют градусами.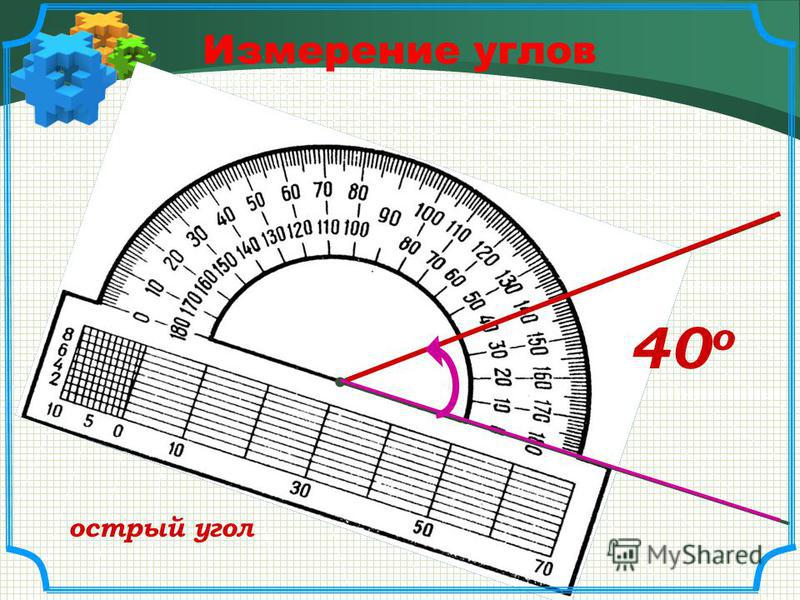 Т.е. градусом называют долю развернутого угла.
Т.е. градусом называют долю развернутого угла.
Градусы обозначают таким знаком °.
Каждое деление шкалы транспортира равно 1°.
Кроме делений по 1° на транспортире есть еще деления по 5° и по 10°.
Рассмотрим на конкретном примере:
Вершина О угла АОВ на рисунке находится в центре полуокружности;
Луч ОА проходит через нулевую отметку (начало отсчета), а луч ОВ проходит через отметку 120. Поэтому угол АОВ равен 120°. Пишут: АОВ=120°
Прямой угол составляет половину развернутого угла, то он содержит 180÷2, т.е. 90°. Прямой угол равен 90°.
Если градусная мера угла меньше 90°, то такой угол называют острым.
А если градусная мера угла больше чем 90°, но меньше 180°, то такой угол называют тупым.
Отсюда можно сделать вывод, что любой острый угол меньше прямого, а любой тупой угол больше прямого угла. Равные углы имеют равные градусные меры, больший угол имеет большую градусную меру, а меньший угол имеет меньшую градусную меру.
Чтобы построить угол АВС равный 70°, необходимо начертить луч ВС, наложить транспортир так, чтобы центр полуокружности совпал с точкой В — началом луча ВС, а сам луч пошел по линии транспортира. Поставим точку А против штриха с отметкой 70 и проведем луч ВА. Получили угол АВС, содержащий 70°.
§ 3 История возникновения приборов для измерений
К сожалению, история не сохранила имя ученого, который изобрел транспортир — возможно в древности этот инструмент имел совсем другое название. Современное название, к которому мы привыкли, переводится с французского, как «переносить».
Древние ученые проводили свои измерения не только транспортиром — ведь этот инструмент неудобен для измерений на местности и решения конкретных практических задач, например, связанных со строительством. А ведь они и являлись главным предметом интереса древних геометров. Изобретение первого инструмента, который бы позволял измерять углы на местности, является заслугой древнегреческого ученого Герона Александрийского. Он описал инструмент — диоптр. Но прогресс не стоит на месте и в ХVII веке был изобретен прибор нивелир, а в следующем веке английским механиком был изобретен другой прибор — теодолит.
Он описал инструмент — диоптр. Но прогресс не стоит на месте и в ХVII веке был изобретен прибор нивелир, а в следующем веке английским механиком был изобретен другой прибор — теодолит.
Однако усовершенствование инструментов для измерения углов связано не только с проведением строительных работ. С древнейших времен люди путешествовали, познавая окружающий мир. И естественно, что путешественникам необходимо было уметь ориентироваться в пространстве.
Долгие века основным ориентиром были звезды. Но со временем появился первый инструмент это — астролябия.Астролябия — это угломерный прибор, служивший до начала восемнадцатого века для определения положений светил на небе. Создание астролябии приписывают Евдоксу. Но в 1731 году английский оптик Джон Хэдли усовершенствовал астролябию. Новый прибор, получивший название октант, позволял решить проблему измерения широты на движущемся судне. Но октанту не досталась слава и долгая жизнь астролябии. Был изобретен секстант — это наиболее совершенный прибор для измерения угловых координат небесных тел того времени.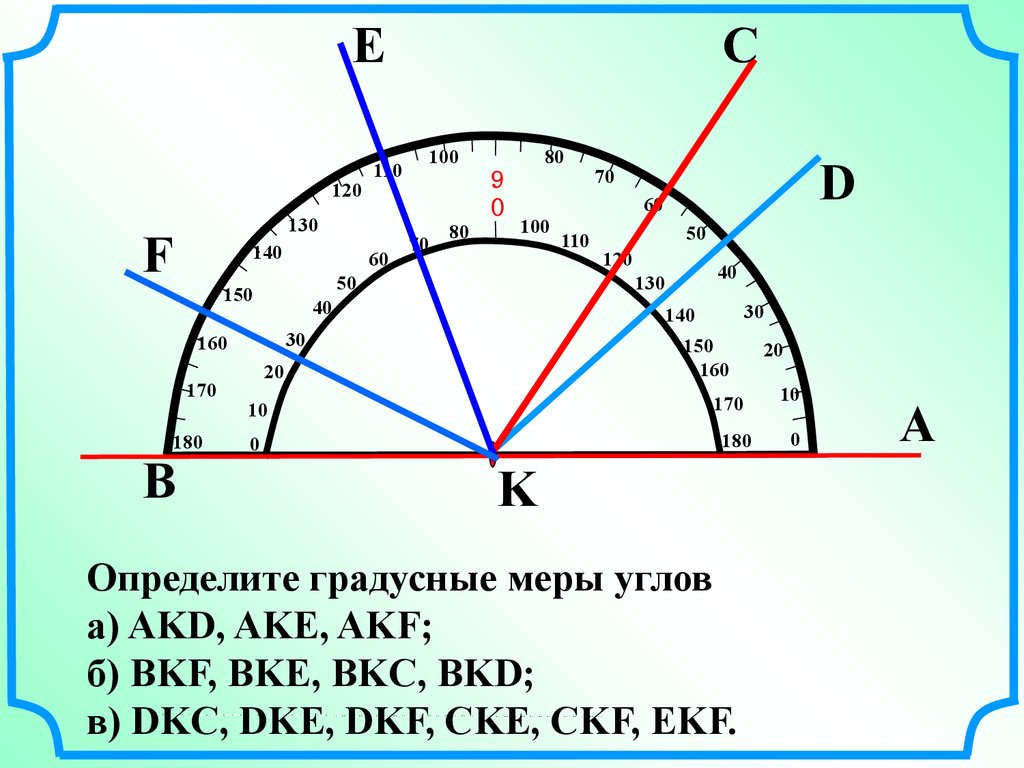 Изобретение секстанта приписывается Исааку Ньютону. Этот прибор позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью. Вот такая история возникновения различных приборов для измерения углов не только на чертежах, но и на любой местности, включая даже небесное пространство!
Изобретение секстанта приписывается Исааку Ньютону. Этот прибор позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью. Вот такая история возникновения различных приборов для измерения углов не только на чертежах, но и на любой местности, включая даже небесное пространство!
Итак, на этом уроке вы познакомились с единицами измерения углов — градусами, а также узнали, как можно измерять углы с помощью транспортира.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. — 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
- Математика.
 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.: ил.
5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.: ил.
Использованные изображения:
Условно выделим в транспортире две части — «линейку», называемую также прямолинейной шкалой (нижняя часть на рисунке), и полукруга, называемого также угломерной шкалой. На полукруге находятся метки градусов от 0° до 180°. Назовем разделение на градусы «градусной сеткой».
Транспортиры бывают разного вида, но использование их сводится к следующему. У транспортира есть центральная метка. На рисунке выше это маленький кружок с отверстием в центре. Однако центральная метка может обозначаться просто черточкой. Эту метку нужно совместить с вершиной угла. При этом одна из сторон угла должна пройти через метку с числом 0 на полукруге транспортира.
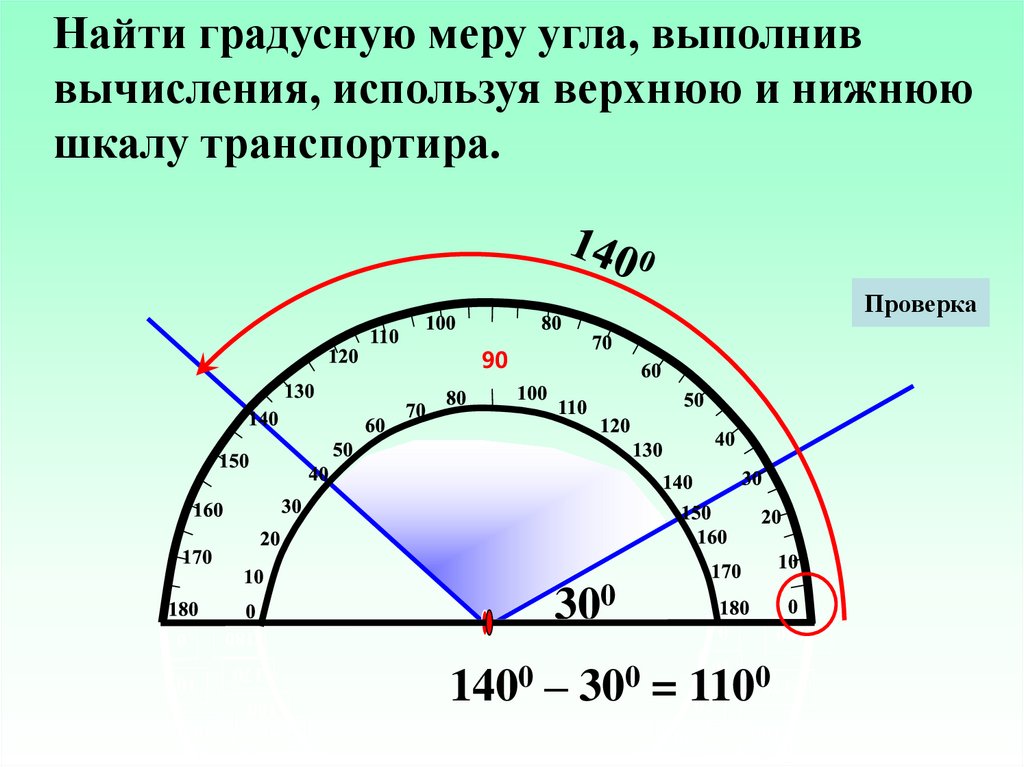
На транспортире может быть две «нулевых» метки: справа и слева. Понятно, что следует смотреть на ту, через которую проходит сторона угла. Но самое главное, понять на какую градусную сетку смотреть при измерении величины угла: верхнюю или нижнюю.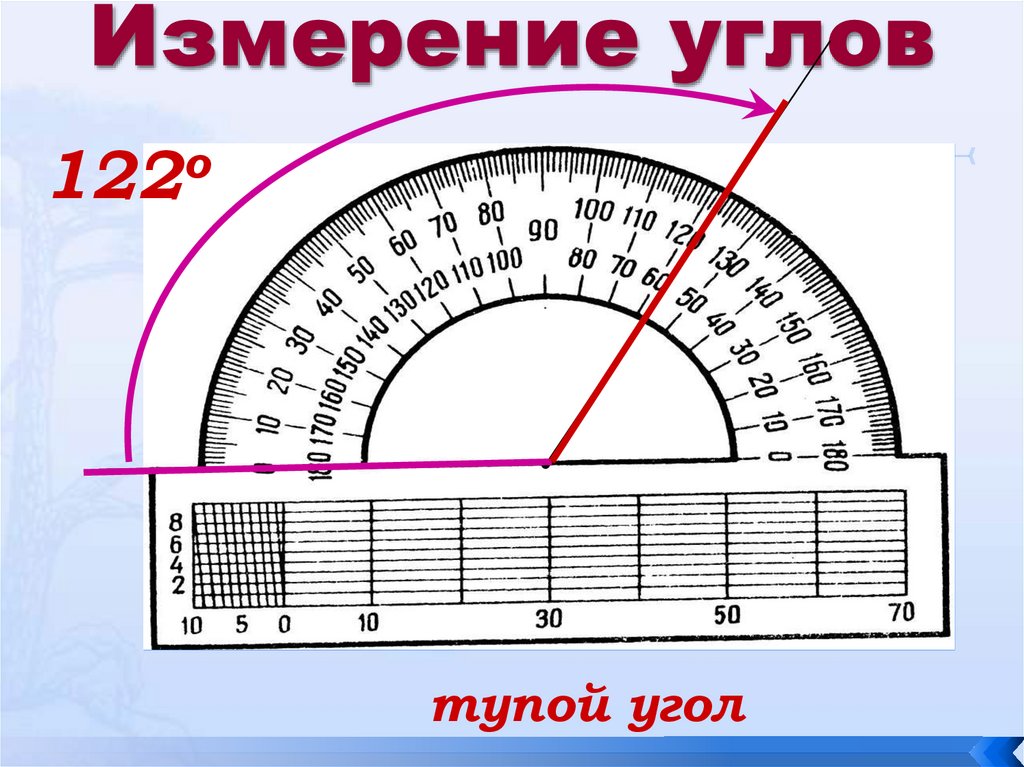 Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).
Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).
Итак, одна сторона угла должна пройти через метку 0, а вторая сторона угла должна оказаться со стороны полукруга (угломерной шкалы), то есть как бы пересекать его.
По тому месту, где вторая сторона угла пересекает угломерную шкалу транспортира, определяется величина угла.
Измерение угла транспортиром
- Оцените, к какому типу относится интересующий вас угол. Углы можно разделить на три класса: острые, тупые и прямые.
Острые углы относительно узки (менее 90 градусов), тупые углы шире (более 90 градусов), а величина прямых углов составляет 90 градусов (их стороны перпендикулярны друг другу). Оцените на глаз, к какому типу принадлежит тот угол, который вы собираетесь измерить. Предварительная оценка поможет вам определить необходимый диапазон и правильно выбрать шкалу транспортира.

На первый взгляд мы можем сказать, что выше изображен острый угол, то есть его величина меньше 90 градусов. - Приложите центр транспортира к вершине измеряемого угла. В середине транспортира есть небольшое отверстие. Приложите транспортир к углу так, чтобы это отверстие совпало с вершиной угла.
- Поверните транспортир так, чтобы одна из сторон угла совпала с основанием инструмента. Не спеша поворачивайте транспортир и следите за тем, чтобы вершина угла оставалась в центре. В результате одна из сторон угла должна совместиться с основанием транспортира.
При этом вторая сторона угла должна пересекать дугу транспортира (его округлую часть). - Проследите за второй стороной угла, которая пересекает дугу транспортира. Если вторая сторона не доходит до дуги инструмента, продлите ее. Можно также приложить к этой стороне угла лист бумаги, который доходил бы до дуги транспортира. Пересекаемое число покажет вам величину угла в градусах.
- В приведенном выше примере величина угла составляет 70 градусов.

транспортир с линейкой
При этом мы пользуемся меньшей шкалой, так как определили ранее, что имеем дело с острым углом, то есть его величина не превышает 90 градусов. Для тупых углов следует использовать более крупную шкалу со значениями больше 90 градусов.
- На первых порах можно путаться со шкалой. Большинство транспортиров имеют две шкалы, одну на внутренней и вторую на внешней стороне округлой части. Это сделано для того, чтобы было удобно измерять углы как левой, так и правой ориентации.
Достаточно взять обычные школьные принадлежности – карандаш и бумагу, линейку, транспортир и циркуль – и можно начертить любую геометрическую фигуру, будь то квадрат, овал, треугольник. Однако бывают случаи, когда чертежных инструментов под рукой нет совсем или их количество ограничено, но даже в этом случае можно сделать нужный чертеж.
Вам понадобится
- — линейка;
- — карандаш;
- — бумага;
- — циркуль;
- — транспортир;
- — прямоугольные треугольники
Инструкция
- Если под рукой нет ничего кроме листа бумаги и карандаша, то можно обойтись даже этими принадлежностями.
 Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°.
Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°. - Можно начертить угол с помощью прямоугольных треугольников, которые могут быть разными – с углами 90°, 45°, 45° и 90°, 60°, 30°. Возьмите треугольник (с углами 90°, 45°, 45°) и обведите на листе бумаги острый угол в 45°. Если имеется только треугольник с углами 90°, 60°, 30°, то на другом листе бумаги обведите прямой угол, вырежьте его, сложите пополам и обведите на нужном чертеже. Это и будет угол в 45°.
- Самым точным будет вариант построения, при котором используется транспортир. Начертите на листе бумаги линию, отметьте на ней угловую точку, приложите транспортир и отметьте точкой 45° , после чего соедините их между собой.

- Интересно, что даже с помощью циркуля можно также изобразить угол в 45° . Для этого достаточно иметь перед собой изображенный угол в 90° (например, с помощью прямоугольного треугольника или путем сгибания бумаги вчетверо). Затем от угловой точки циркулем проведите окружность.
Как правильно пользоваться угломером?
В месте пересечения окружности и сторон прямого угла отметьте точки. Теперь от каждой из двух точек тем же раствором циркуля сделайте еще две окружности. В месте их пересечения получится точка, которую соедините с угловой, в результате чего получится два угла по 45° .
© CompleteRepair.Ru
Транспортир
Н.Е. Жуковский В математике есть своя красота, как в живописи и поэзии.
Что такое транспортир? Транспорти́р — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°.
презентация по теме «Транспортир», история и правила пользования
В некоторых моделях — от 0 до 360°.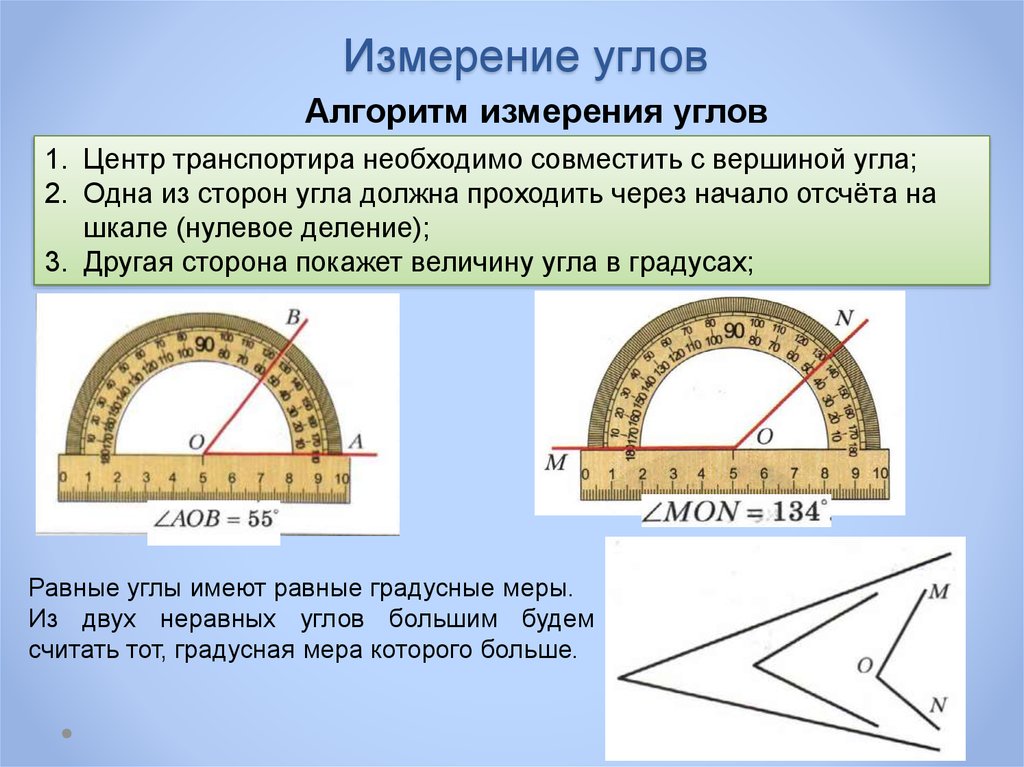 .
.
Из чего делают транспортиры? Транспортиры изготавливаются из стали,пластмассы,дерева и других материалов. .
История транспортира История не сохранила имя ученого, который изобрел транспортир – возможно в древности этот инструмент имел совсем другое название. Современное название происходит от французского слова ”ТRANSPORTER”, что означает “переносить”. Предположительно, транспортир изобрели в древнем Вавилоне. .
Разновидности транспортиров Полукруговые (180 градусов) — наиболее простые и древние транспортиры. Круговые (360 градусов). Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям. Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр. Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра. .
.
Для чего нужен транспортир? Транспортир — инструмент, широко используемый в геометрии. При этом обойтись без этого инструмента достаточно трудно как школьникам, решающим свои первые задачи, так и инженерам, выполняющим сложные геометрические построения. Чаще всего транспортир используется для получения градусной меры угла.Без транспортира мы не сможем измерить угол. .
Как пользоваться транспортиром? Для измерения угла необходимо поместить его вершину в точку начала отсчета, обозначенную на линейке транспортира. Затем необходимо обратить внимание на то, чтобы сторона угла, направленная на угломерную шкалу, пересекала ее. В случае, если длина этой стороны оказывается недостаточной, следует продлить ее до пересечения угломерной шкалы. После этого нужно посмотреть, на каком значении сторона угла пересекает указанную шкалу. В случае, если измерению подвергается острый угол, искомое значение будет меньше 90°, а при измерении тупого угла следует пользоваться той частью шкалы, которая содержит деления, превышающие 90°. Аналогичным образом осуществляется построение углов при помощи транспортира. Сначала следует провести линию, которая будет представлять собой одну из сторон, а ее окончание, которое станет вершиной, поместить в точку отсчета. Затем на угломерной шкале точкой нужно отметить нужную величину угла, который может быть как острым, так и тупым. После этого, убрав транспортир, соедините вершину будущего угла с проставленной точкой: в результате вы получите искомый угол. .
Аналогичным образом осуществляется построение углов при помощи транспортира. Сначала следует провести линию, которая будет представлять собой одну из сторон, а ее окончание, которое станет вершиной, поместить в точку отсчета. Затем на угломерной шкале точкой нужно отметить нужную величину угла, который может быть как острым, так и тупым. После этого, убрав транспортир, соедините вершину будущего угла с проставленной точкой: в результате вы получите искомый угол. .
Спасибо за внимание!
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
- Образовательные
:- познакомить учащихся с единицей измерения
углов, с прибором для измерения углов; - научить пользоваться транспортиром.

- познакомить учащихся с единицей измерения
- Развивающие
:- развивать внимание, мышление учащихся;
- развивать самостоятельность учащихся,
используя проблемные ситуации, творческие
задания; - развивать познавательный интерес к предмету.
- Воспитательные
:- воспитывать чувство взаимоуважения;
- воспитывать у учащихся навыки учебного труда.
ХОД УРОКА
I. Организационный момент
II. Вступительное слово учителя
Мы познакомимся с измерительным прибором (как
он называется, вы узнаете немного позже),
научимся с его помощью измерять, а затем и
строить углы. Вы покажите свои знания, докажите
насколько внимательны.
Будем учиться не только математике, но и умению
общаться, уважению друг к другу.
Для того чтобы достичь наших целей, вы должны
быть волевыми, настойчивыми, целеустремленными,
поэтому эпиграфом нашего урока будут слова:
III. Устная работа
Какие из углов, изображенных на рисунке,
являются:
а) острыми;
б) тупыми;
в) есть ли среди этих углов прямые?
О каком угле мы с вами еще не вспомнили? [О
развернутом]
Какой угол называется развернутым? Острым?
Прямым? Тупым?
Мы знаем, что два угла можно сравнивать друг с
другом.
Какой способ для этого мы использовали?
[Наложение]
Но углы, также как и отрезки, можно сравнивать
не только наложением, но и с помощью измерения.
IV. Изучение нового материала
Для построения и измерения углов используют
специальный прибор. Как он называется, вы
узнаете, отгадав кроссворд.
1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие
угол.
4. Угол, который образуют два дополнительных
друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину
развернутого угла.
7. Инструмент, который используют для
построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше
развернутого.
10. Результат умножения.
11. Результат вычитания.
Учитель демонстрирует учащимся транспортир
или показывает на плакате:
– Для измерения углов применяют транспортир.
Положите перед собой транспортиры. Вы видите,
какие они разные, но у всех есть нечто общее, о чем
мы сейчас будем говорить.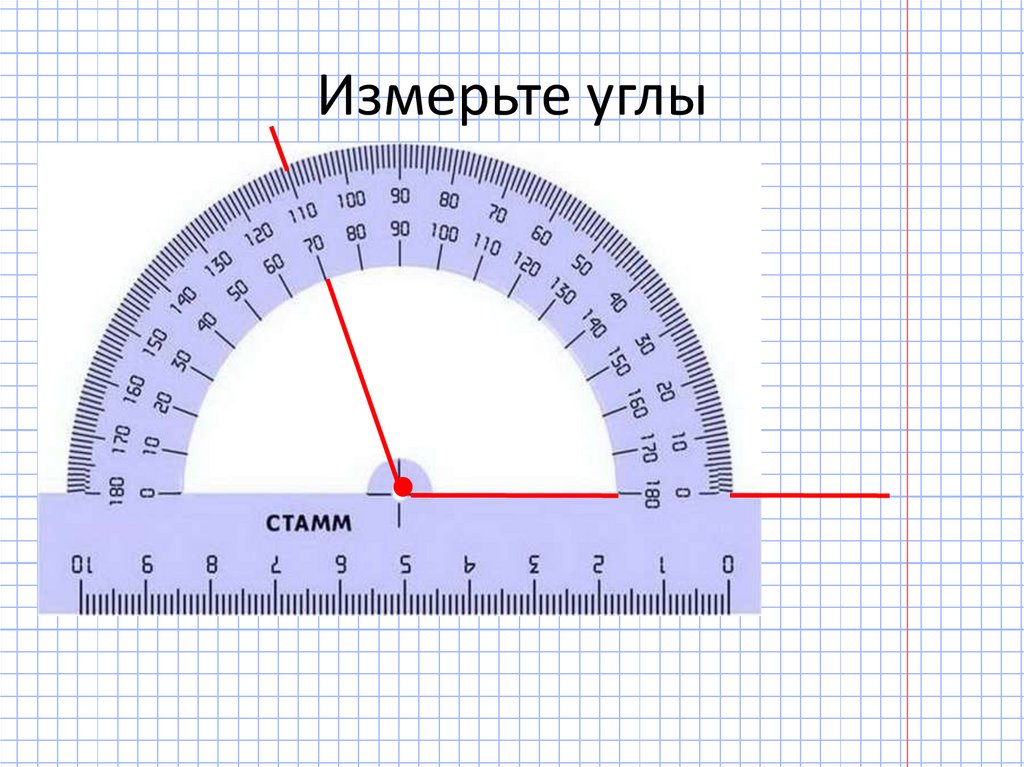
Слайд 5. Итак, шкала
транспортира.
Она расположена на полуокружности и
пронумерована
от 0 до 180. Бывают шкалы двойные: нумерация идет
слева направо и справа налево.
Слайд 6. Также есть круглые транспортиры, шкала
идет по кругу от 0 до 360, но она также разделена на
две полуокружности.
Центр этой полуокружности отмечен на
транспортире точкой или черточкой. Найдите на
своем транспортире центр и покажите его.
Штрихи шкалы транспортира делят
полуокружность на 180 равных частей. Лучи,
проведенные из центра полуокружности через эти
штрихи, образуют 180 углов, каждый из которых равен
доле
развернутого угла. Такие углы называют
градусами.
Слайд 7. Итак, градусом
называют долю
развернутого угла. Градусы обозначают знаком
°. Каждое деление шкалы транспортира равно 1°.
Историческая справка
Слово «градус»
– латинское,
означает «шаг», «ступень». Измерение углов в
градусах появилось более 3 тыс. лет назад в
лет назад в
Вавилоне. В расчетах там использовались
шестидесятеричная система счисления,
шестидесятеричные дроби.
С этим связано, что вавилонские математики и
астрономы, а вслед за ними греческие и индийские,
полный оборот (окружность) делили на 360 частей – градусов
(шесть раз по шестьдесят), каждый градус – на 60
минут
, а минуту – на 60 секунд
:
Объяснение учителя
(с демонстрацией
на доске), как с помощью транспортира можно
измерить угол.
– Как измеряют углы с помощью транспортира
?
1) Нужно вершину угла совместить с центром
транспортира.
2) Одна сторона угла должна проходить через
нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу.
Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть
величина этого угла.
Если у транспортира есть две шкалы, то надо
смотреть на отметку той шкалы, через ноль которой
проходит одна из сторон угла.
V.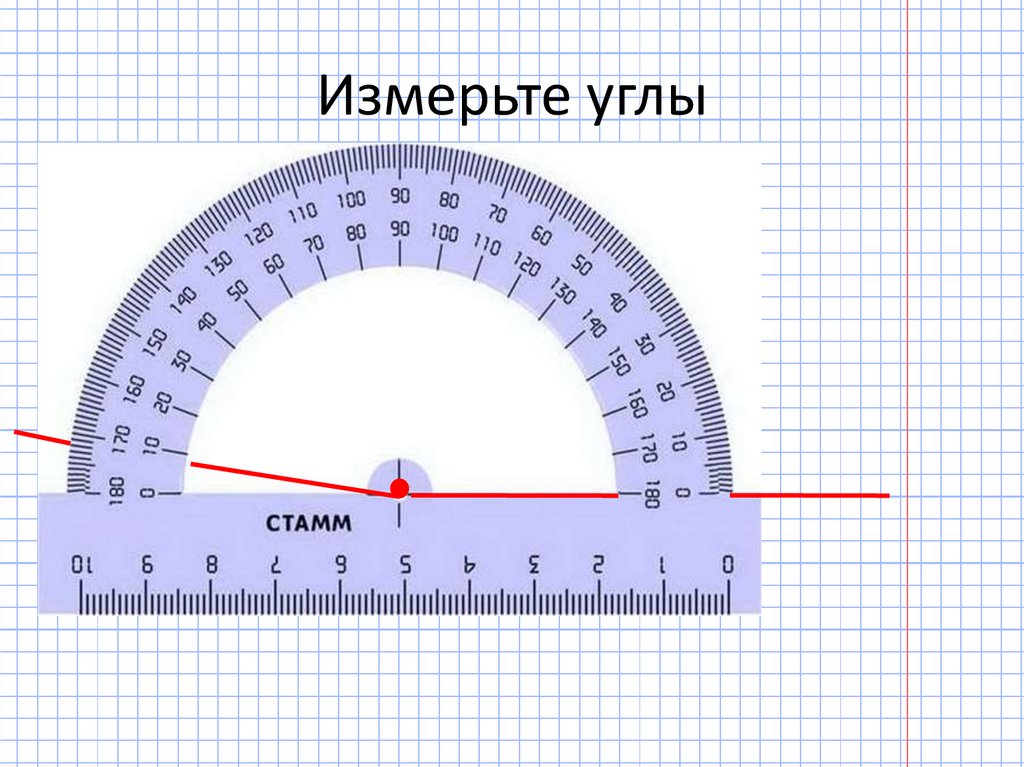 Практическая работа
Практическая работа
Каждому ученику выдается набор углов: острый,
прямой, тупой и развернутый.
Задания
- Выберите из предложенных вам углов острый,
тупой, прямой, развернутый. - Измерьте их градусную меру и запишите в
тетрадях эти данные. - Сделайте вывод о градусной мере:
а) развернутого угла;
б) прямого угла;
в) острого угла;
г) тупого угла.
Вывод:
VI. Физкультурная пауза
- Покажите руками угол 90°, 180°.
- Покажите руками острый угол, тупой угол.
- Покажите рукой, где вокруг нас есть прямые углы.
- Повернитесь на 180°. А теперь на 90°.
Продолжаем работать.
Задание:
Начертите в тетради угол
любой величины. Предложите соседу по парте его
измерить.
VII. Работа по карточкам
У всех учеников карточки с одинаковым заданием.
Задание:
Измерьте углы и запишите
результаты измерений в тетрадях.
Слайд11.
Задание:
Выполняется устно с
использованием модели часов.
Какой угол образуют часовая и минутная стрелки
часов:
а) в 3
ч;
в) в 10
ч;
д) в 2 ч 30 мин;
б) в 5
ч;
г) в 6
ч;
е) в 5 ч 30 мин?
Задача №1652
Луч ОС лежит внутри угла АОВ,
причем АОС = 37°, ВОС = 19°?.
Чему равен угол АОВ°
Слайды 13, 14, 15.
VIII. Итог урока
IX. Задание на дом
п. 42, №1651, №1683, №1672.
Измерение углов — определение, использование транспортира, примеры
Измерение углов выполняется с помощью простого геометрического инструмента, такого как транспортир. Транспортир используется чаще, чем циркуль. Измерение углов полезно для того, чтобы точно знать, в какой мере находится угол. В геометрии существуют различные типы углов, с которыми мы сталкиваемся в повседневной жизни, и с помощью этих инструментов мы можем определить измерения углов . Давайте посмотрим, как измерить угол, необходимые шаги и решим несколько примеров.
Давайте посмотрим, как измерить угол, необходимые шаги и решим несколько примеров.
| 1. | Что такое измерение углов? |
| 2. | Измерение углов с помощью транспортира |
| 3. | Построение и измерение углов с помощью транспортира |
| 4. | Единицы измерения углов |
| 5. | Часто задаваемые вопросы об измерении углов |
Что такое измерение углов?
Измерение углов выполняется с помощью основных геометрических инструментов, таких как транспортир и циркуль. Эти инструменты помогают найти точную меру угла. Транспортир помогает точно измерить угол, а циркуль помогает в построении угла. Измерение углов производится тремя способами — градусами, радианами и оборотами. Давайте посмотрим, каковы эти три способа измерения углов.
Градусы
Градус — единица измерения угла, измеряемая с помощью геометрического инструмента — транспортира. Градус обозначается символом «°». Окружность полностью вращается на 360°, и градус является частью этого вращения на 360°, поскольку он делится на 360 равных частей. Разные углы с разными градусами: 30°, 45°, 90° и так далее. И читается как 30 градусов, 45 градусов, 90 градусов и т. д.
Градус обозначается символом «°». Окружность полностью вращается на 360°, и градус является частью этого вращения на 360°, поскольку он делится на 360 равных частей. Разные углы с разными градусами: 30°, 45°, 90° и так далее. И читается как 30 градусов, 45 градусов, 90 градусов и т. д.
Радиан
Радиан — это еще одна единица измерения угла, которая используется вместо градусов, когда угол необходимо измерять в радианах. По определению, радиан — это отношение длины дуги, на которую опирается угол окружности, к длине радиуса той же окружности. Другими словами, радиан — это угол, образуемый дугой длины радиуса того же круга в центре, и соотношение даст радианную меру угла. Радиан обозначается как рад или c и записывается как 1,7 радиан или 1,7 рад или 1,7 c . Половина круга составляет 180°, что составляет π радиан, а один полный оборот равен 2π радианам.
Обороты
Обороты — простейшая форма измерения углов. В градусах оборот также является единицей 360 °, поскольку угол в основном является подразделением окружности, а не суммой нескольких градусов. Например, при измерении оборотов мы можем сказать, что прямой угол равен четверти окружности, а в градусах угол читается как прямой угол, равный 9.0°.
Например, при измерении оборотов мы можем сказать, что прямой угол равен четверти окружности, а в градусах угол читается как прямой угол, равный 9.0°.
Измерение углов с помощью транспортира
Угол измеряется с помощью двух геометрических инструментов — транспортира и циркуля. В то время как транспортир можно использовать как для построения, так и для измерения, циркуль в основном используется для построения угла. Транспортир считается одним из самых важных геометрических инструментов, поскольку он помогает измерять углы как в градусах, так и в радианах. Когда мы смотрим на транспортир, мы видим измерения от 0 до 180 слева направо по внешнему краю и от 180 до 0 справа налево по внутреннему краю. Измерения по обоим краям составляют до 180°.
При измерении с помощью транспортира измерение обычно производится в градусах. Если угол находится на левой стороне транспортира, мы используем измерение внешнего края, а если угол находится на правой стороне транспортира, мы используем измерения внутреннего края. Шаги для измерения угла:
Шаги для измерения угла:
- Шаг 1: Поместите центр транспортира в вершину угла.
- Шаг 2: Совместите одну сторону угла с нулевой линией транспортира.
- Шаг 3: Угол равен количеству градусов, пересекаемых транспортиром.
Давайте рассмотрим пример. Измерьте ∠AOB.
Шаг 1: Совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на нижней дуге транспортира.
Следовательно, ∠AOB = 60°. Поскольку мера больше 0° и меньше 90°, можно сказать, что угол ∠AOB острый.
Пример: Используя тот же пример, что и выше, давайте измерим угол с другой стороны транспортира. Измерьте ∠AOC.
Шаг 1: Совместите транспортир с лучом CO, как показано ниже. Начните чтение с отметки 0 ° в левом нижнем углу транспортира.
Начните чтение с отметки 0 ° в левом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на верхней дуге транспортира.
Следовательно, ∠AOC = 120°. Поскольку мера больше 90° и меньше 180°, мы можем сказать, что угол ∠AOC тупой.
Построение и измерение углов с помощью транспортира
Транспортир можно использовать не только для измерения, но и для построения углов. Это помогает как точно измерить углы, так и научиться пользоваться транспортиром. Давайте посмотрим, как нарисовать 40 ° с помощью транспортира.
- Нарисуйте базовую линию AB.
- Отметьте точку O и поместите центр транспортира в точку O.
- Совместите базовую линию транспортира с линией OB.
- Во внутренних показаниях найдите угол 40º и отметьте его как точку C.
- Теперь, используя шкалу, соедините O и C.
- ∠COB = 40°
Чтобы измерить 230º, угол отражения, мы можем записать его как 180° + 50°.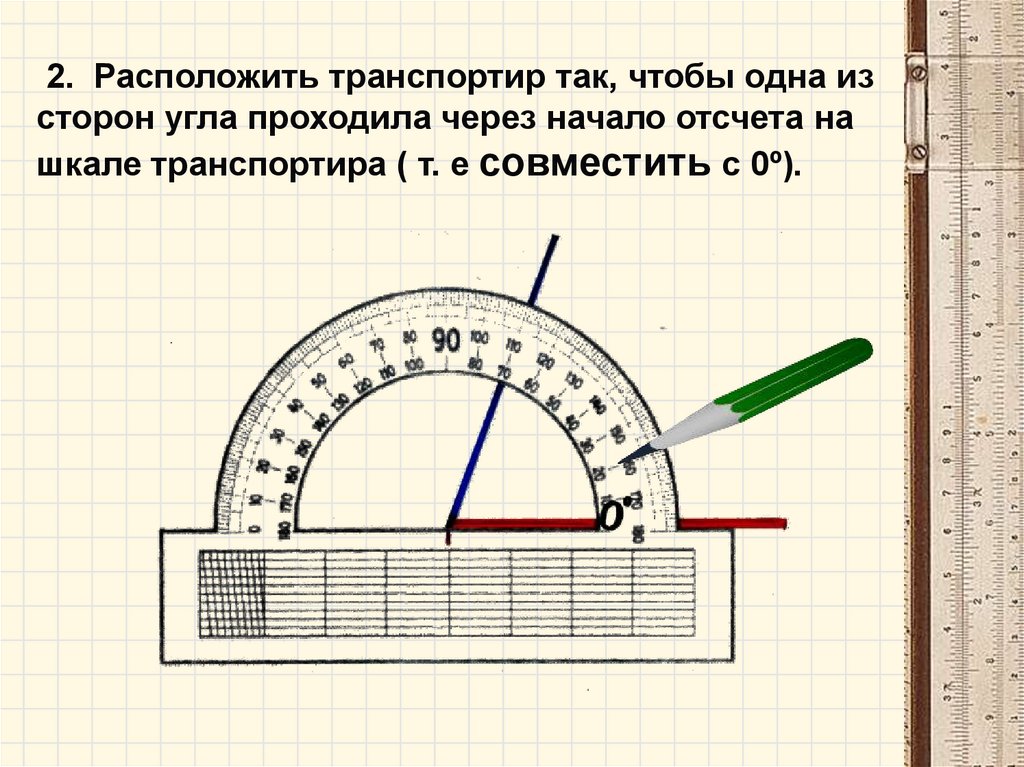 Мы можем просто перевернуть транспортир вдоль базовой линии и затем отметить 50°. 180° + 50° = 230°
Мы можем просто перевернуть транспортир вдоль базовой линии и затем отметить 50°. 180° + 50° = 230°
Единицы измерения углов
Углы в геометрии можно измерять, используя в основном две единицы измерения:
- Радианы
- градусов
Радианы — это единица измерения углов в системе СИ, наиболее часто используемая в концепции тригонометрии. Другая единица, используемая для измерения углов, — градусы, обозначаемые °, — обычно используется в геометрии. Один оборот равен 360 градусам или 2π радианам.
Важные замечания по измерению углов
- Измерение углов выполняется с помощью основных геометрических инструментов, таких как транспортир и циркуль.
- Углы в геометрии можно измерять, используя в основном две единицы измерения — радианы и градусы.
Похожие статьи
- Угол 180 градусов
- Центральный угол
- Дополнительные уголки
- Радиан в Градус
Часто задаваемые вопросы об измерении углов
Что подразумевается под измерением углов?
В геометрии процесс считывания углов или определения точного угла называется измерением углов . Лучший способ измерения углов — использование геометрического инструмента, известного как транспортир. Это полукруглый инструмент с разметкой от 0° до 180°.
Лучший способ измерения углов — использование геометрического инструмента, известного как транспортир. Это полукруглый инструмент с разметкой от 0° до 180°.
Каковы 3 способа измерения углов?
В геометрии существует 3 способа или единицы измерения углов: градусы, радианы и обороты.
- Градусы: Самый распространенный способ измерения углов — градусы. Окружность полностью вращается на 360°, и градус является частью этого вращения на 360°, поскольку он делится на 360 равных частей.
- Радиан: Радиан — это угол, образуемый дугой длины радиуса того же круга в центре, и соотношение дает радианную меру угла.
- Оборот: Оборот — это мера угла, когда он поворачивается на одну сторону, завершая 360°.
Как лучше всего измерять углы?
Углы лучше всего измерять с помощью транспортира. Шаги:
- Поместите центр транспортира в вершину угла.
- Совместите одну сторону угла с нулевой линией транспортира.
- Угол равен количеству градусов, пересекаемых транспортиром.

Как измерить угол без транспортира?
Чтобы измерить угол без транспортира, воспользуемся простой линейкой. Сначала мы соединяем два луча в точке, образуя треугольник. Вот шаги:
- Нарисуйте линию, соединяющую два луча угла.
- Измерьте длину основания треугольника с помощью линейки. Также называется бегом.
- Измерьте длину прямой стороны треугольника с помощью линейки. Также называется подъемом.
- После того, как обе длины получены, мы используем простую формулу уклона, т.е. уклон = подъем/прогон.
- Введите значение наклона в научный калькулятор, затем нажмите кнопку обратного загара.
Каковы различные меры углов?
Различные меры или типы углов:
- Острый угол: Измерьте от 0° до 90°.
- Тупой угол: Измерьте от 90° до 180°
- Прямой угол: мера точно равна 90°.
- Прямой угол: мера точно равна 180°.
- Угол отражения: Измеряйте от 180° до 360°.

- Полный или полный угол: измерение точно равно 360°.
Какой инструмент используется для измерения углов?
Наиболее часто используемым инструментом для измерения углов является транспортир. Транспортир считается важным измерительным инструментом, имеющим форму полукруга.
Какие единицы используются для измерения углов?
Углы в геометрии можно измерять, в основном, двумя единицами измерения — радианами и градусами.
Что такое угол? Определение, транспортир, примеры, факты
Мера угла Определение
Угол образуется, когда две прямые или лучи пересекаются в одной точке. Общая точка называется вершиной.
В геометрии мера угла может быть определена как мера угла, образованного двумя лучами или плечами в общей вершине.
Например, на рисунке ниже желтая область измеряет размах угла.
Родственные игры
Как найти угол?
Углы измеряются в градусах (°) с помощью транспортира. Транспортир — это измерительное устройство, которое используется для вычисления или рисования углов в градусах.
Транспортир — это измерительное устройство, которое используется для вычисления или рисования углов в градусах.
Например, на изображении ниже мы видим, что с помощью транспортира черная стрелка указывает на 100°, пересекая 90°. Следовательно, мера угла равна 100°.
Чтобы определить угол с помощью транспортира, выполните следующие действия:
- Расположите среднюю точку или середину транспортира на вершине угла.
- Поместите одну сторону угла на отмеченную нулем линию транспортира (в точке, где вы видите цифру 0).
- Найдите градусную меру, при которой другая сторона транспортира указывает угол.
Связанные рабочие листы
Типы углов
В геометрии существует много видов углов: острые, тупые, изогнутые, прямые и прямые. Каждый угол имеет разную меру.
Существуют также специальные типы угловых пар. Давайте сначала посмотрим на различные типы углов.
Типы углов на основе измерения
Прямой угол
Угол между двумя лучами, равный ровно 90°, называется прямым углом.
Острый угол
Острый угол образуется, когда два луча пересекаются в вершине и образуют угол меньше 90°. Некоторые примеры острых углов: 20°, 40°, 60° и 80°.
Тупой угол
Тупые углы – это любые углы, градусная мера которых больше 90° и меньше 180°. Некоторые примеры тупых углов включают 110°, 130°, 145° и 165°.
Прямой угол
Прямой угол, как следует из названия, представляет собой прямую линию. Два луча, образующие прямой угол, направлены друг против друга. Угол между двумя лучами равен 180°. Два смежных прямых угла можно объединить, чтобы получился прямой угол.
Угол рефлекса
Угол рефлекса — это угол больше 180° или меньше 360°. Некоторые примеры рефлекторных углов включают
210° и 250°.
Типы углов на основе поворота
Положительные углы
Угол, определяющий степень поворота луча от его начальной точки до конечного положения в направлении против часовой стрелки, называется положительным углом. Направление против часовой стрелки считается положительным направлением в смысле угла.
Направление против часовой стрелки считается положительным направлением в смысле угла.
Отрицательные углы
Отрицательные углы — это углы, которые повернуты по часовой стрелке от основания.
Типы пар углов
Пара углов представляет собой комбинацию двух углов. Давайте узнаем больше о различных парах углов в геометрии.
Смежные углы
Чтобы два угла считались смежными, должны выполняться следующие условия:
- Два угла имеют одну и ту же вершину.
- Два угла имеют одно плечо.
Дополнительные углы
Дополнительные углы — это углы, сумма которых равна 90°. Дополнительные углы могут быть смежными или несмежными.
Например, на данном изображении показаны смежные и несмежные дополнительные углы.
На первом изображении сумма углов равна $30°+ 60°=90°$
На втором изображении сумма углов равна $50°+ 40°=90°$
Дополнительные углы
Дополнительные углы — это углы, сумма которых равна 180°, то есть сумма их угловых величин равна 180°.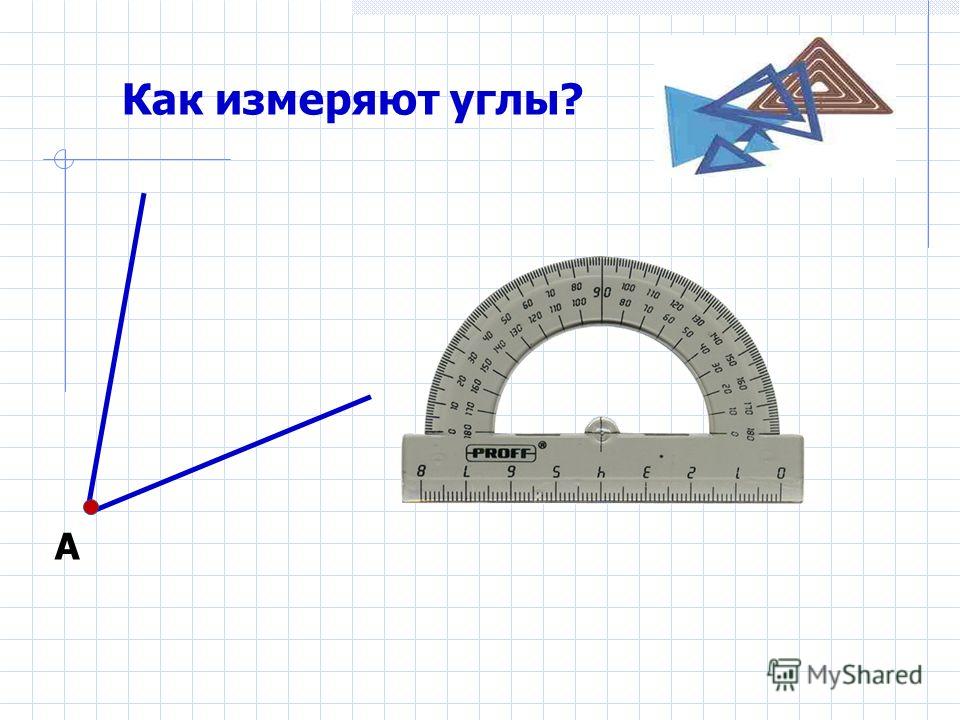
Если два дополнительных угла примыкают друг к другу, они называются «углами в линейной паре».
Например, на изображении выше углы в 140° и 40° являются дополнительными и смежными. Таким образом, они образуют линейную пару.
С другой стороны, углы 150° и 30° являются дополнительными, но не смежными.
Соответствующие углы
Рассмотрим две параллельные прямые. Когда они пересекаются другой линией, то есть секущей, углы, образующиеся в соответствующих углах, называются соответствующими углами.
Вертикальные уголки
При пересечении двух прямых углы, противоположные друг другу, равны. Они называются вертикальными углами или вертикально противоположными углами.
Давайте петь!
Острые углы немного меньше, чем обычно.
Угол стены прямой
Тупой угол 2.50 днем
Прямой изгиб в соломе из натриевой извести
Сколько углов, даже у мимов!
Решенные примеры
1. Если ∠A равно 55°, то какой это угол?
Если ∠A равно 55°, то какой это угол?
Решение : $∠A = 55°$
Острый угол образуется, когда два луча пересекаются в вершине и образуют угол, который меньше 90°. Так как угол 55° меньше 90°, то это острый угол.
2. Как называется пара углов размером 55° и 35°?
Решение : Дополнительные углы — это углы, сумма которых равна 90°.
Поскольку сумма этих углов равна $90 ° (55° + 35° = 90°)$, мы называем их дополнительными углами.
3. Если ∠P равно 210°, то какой это угол?
Решение : Угол рефлекса — это угол больше 180° или меньше 360°. Так как ∠ P измеряет 210 °, это рефлекторный угол.
Практические задачи
1
Как называется угол 90°?
Прямой угол
Прямой угол
Острый угол
Тупой угол
Правильный ответ: Прямой угол
В геометрии и тригонометрии прямым углом называется угол, равный точно 90°.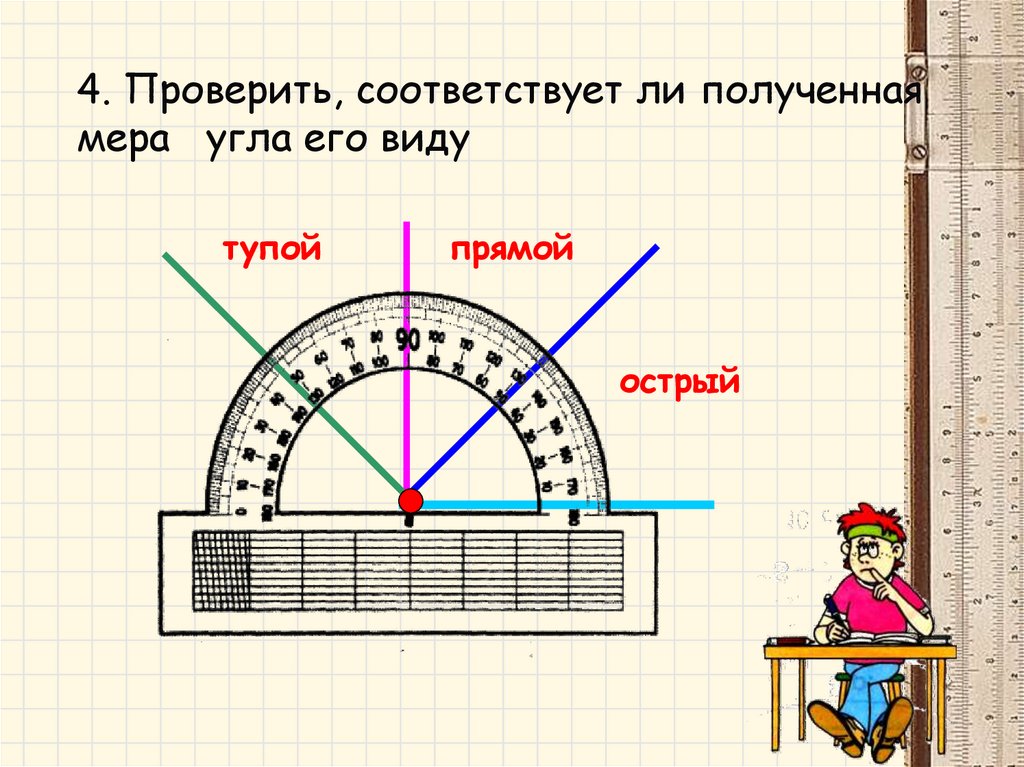

 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.: ил.
5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009. — 270 с.: ил.

 Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°.
Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°.