Коэффициент наклона прямой
Что такое линейная функция и как выглядит ее график мы подробно разбирали здесь.
В этой статье мы остановимся на том, как находить коэффициент наклона прямой.
Как мы знаем, уравнение прямой имеет вид . В этом уравнении коэффициент при отвечает за наклон прямой и называется коэффициентом наклона. Он равен тангенсу угла между прямой и положительным направлением оси .
Внимание! Не просто между прямой и осью , а именно между прямой и положительным направлением оси .
Например, в прямой коэффициент наклона равен , в прямой коэффициент наклона равен .
В уравнении прямой слагаемое, содержащее отсутствует, следовательно, коэффициент при равен нулю. Угол наклона этой прямой к оси равен нулю — прямая параллельна оси .
Если прямая наклонена вправо, то угол между прямой и положительным направлением оси — острый, соответственно, тангенс этого угла больше нуля, и коэффициент .
Например:
Здесь
Если прямая наклонена влево, то угол между прямой и положительным направлением оси — тупой, соответственно, тангенс этого угла меньше нуля, и коэффициент :
Здесь .
Решим две задачи на нахождение коэффициента наклона прямой.
1. Найдите угловой коэффициент прямой, проходящей через точки с координатами (-1;-1) и (1;3).
Решим эту задачу двумя способами.
А). Так как прямая проходит через точки (-1;-1) и (1;3), координаты этих точек удовлетворяют уравнению прямой . То есть если мы координаты каждой точки подставим в уравнение прямой, то получим верное равенство. Так как у нас две точки, получаем систему:
или
Вычтем из второго уравнения первое, и получим , отсюда .
Б). Построим график этой функции. Для этого нанесем данные точки А(-1;-1) и В(1;3) на координатную плоскость и проведем через них прямую:
Коэффициент равен тангенсу угла наклона между прямой и положительным направлением оси , на чертеже это угол :
Чтобы найти рассмотрим прямоугольный треугольник АВС с вершинами в данных точках.
Угол прямоугольного треугольника АВС равен углу (соответственные углы, полученный при пересечении параллельных прямых АС и ОХ секущей АВ):
равен отношению противолежащего катета к прилежащему, то есть
Отсюда
2. Найдите угловой коэффициент прямой, проходящей через точки с координатами (4;0) и (0;8).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (4;0) и (0;8).
Решение с помощью системы уравнений абсолютно аналогично решению предыдущей задачи, можете воспроизвести его самостоятельно.
Выполним это задание с помощью графика.
Нанесем данные токи на координатную плоскость и проведем через них прямую:
Угол между прямой и положительным направлением оси ОХ — это угол :
Коэффициент наклона прямой . Чтобы найти , построим прямоугольный треугольник ВОА:
В этом прямоугольном треугольнике угол — внешний. Мы можем найти тангенс внутреннего угла . .
. Отсюда .
Еще раз! Если прямая наклонена влево, то коэффициент наклона прямой отрицательный.
И.В. Фельдман, репетитор по математике.
Как определить угол наклона потолка?
Для подбора накладок на скошенный потолок вам необходимо знать диаметр основания светильника и угол наклона потолка, в статье расскажем про угол.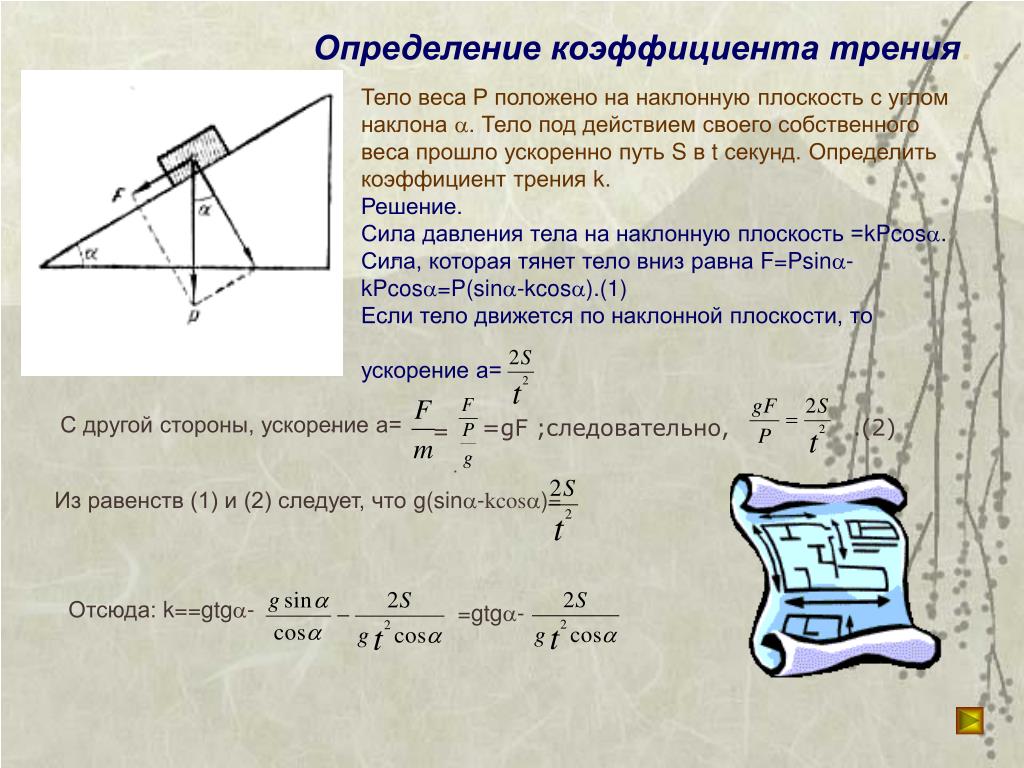
Несмотря на кажущуюся простоту вопроса, иногда вычисление угла наклона потолка вызывает некоторую сложность. Мы компания более чем клиентоориентированная, так что с удовольствием дадим пару вариантов как этот ваш угол мансардного потолка измерить. Перейти в Каталог продукции!
Способ первый и самый простой. В нашу цифровую эпоху многие пользуются смартфонами и в большинстве современных есть различные гироскопические датчики, в первую очередь это применяется в играх, чтобы определять положение телефона в пространстве ) но и для практических нужд этот функционал отлично применяется. Можно скачать (или просто открыть, например, на айфоне оно предустановлено) приложение и с его помощью простым прикладыванием к наклонной плоскости определить угол:
Но даже тут есть маленький нюанс, если вы делаете замеры телефоном именно в точке будущего крепежа накладки, то все хорошо.
Но если вы делаете замер в какой-то другой точке потолка, то может появиться некоторая погрешность, т. к. маленькая площадь поверхности измерения, именно в этом месте может быть, например, какой-то изгиб, незаметный глазу. В этом случае лучше взять какую-нибудь пряму рейку, приложить ее к потолку и уже к ней прикладывать телефон:
к. маленькая площадь поверхности измерения, именно в этом месте может быть, например, какой-то изгиб, незаметный глазу. В этом случае лучше взять какую-нибудь пряму рейку, приложить ее к потолку и уже к ней прикладывать телефон:
Вот уже разницу в 1 градус получили ) К слову, посмотреть ассортимент изделий из заказать можно в разделе Каталог.
Есть еще вариант как сделать замер скоса потолка. Нам понадобится раздвижной транспортир и обычный уровень. Этот способ более сложный, но будет актуален, если под рукой нет смартфона )
Также есть еще вот такие уровни, прикладываете к плоскости и крутите шкалу пока не поймаете баланс, вот и покажет ваш угол:
Надеюсь вам это упростит задачу подбора накладок на скошенный потолок для светильников и люстр.
теория, примеры, решение задач, угол наклона прямой к оси х
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси Ох с их угловым коэффициентом. Допустим, что задана декартова система координат Ох на плоскости.
Определение 1
Угол наклона прямой к оси Ох, расположенный в декартовой системе координат Оху на плоскости, это угол, который отсчитывается от положительного направления Ох к прямой против часовой стрелки.
Когда прямая параллельна Ох или происходит совпадение в ней, угол наклона равен 0. Тогда угол наклона заданной прямой α определен на промежутке [0, π).
Определение 2
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k.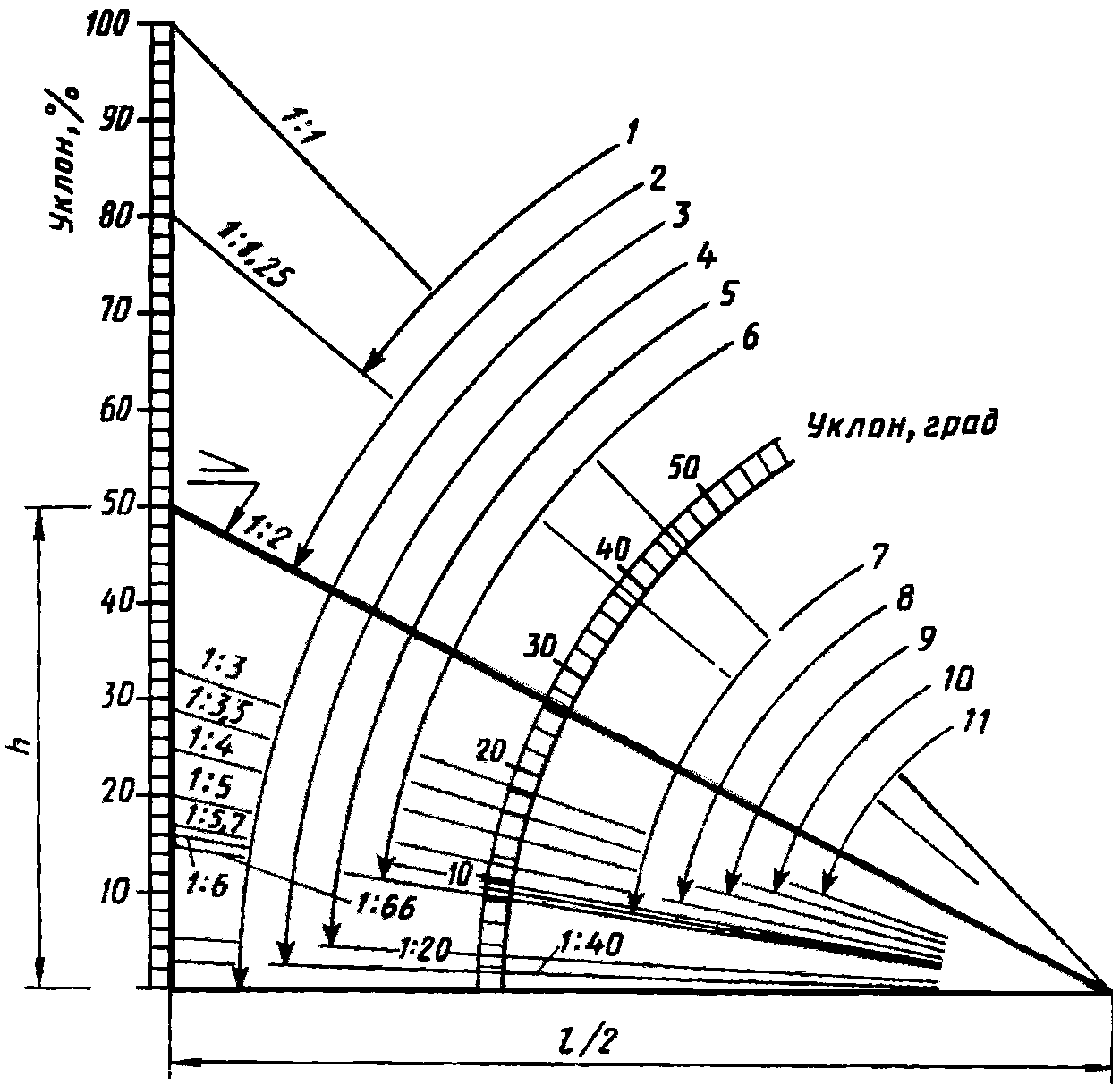 Из определения получим, что k=tg α. Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Из определения получим, что k=tg α. Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Пример 1
Посчитать угловой коэффициент прямой при угле наклона равном 120°.
Решение
Из условия имеем, что α=120°. По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k=tg α=120=-3.
Ответ: k=-3.
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k>0, тогда угол прямой острый и находится по формуле α=arctg k. Если k<0, тогда угол тупой, что дает право определить его по формуле α=π-arctgk.
Если k<0, тогда угол тупой, что дает право определить его по формуле α=π-arctgk.
Пример 2
Определить угол наклона заданной прямой к Ох при угловом коэффициенте равном 3.
Решение
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к Ох меньше 90 градусов. Вычисления производятся по формуле α=arctg k=arctg 3.
Ответ: α=arctg 3.
Пример 3
Найти угол наклона прямой к оси Ох, если угловой коэффициент = -13.
Решение
Если принять за обозначение углового коэффициента букву k, тогда α является углом наклона к заданной прямой по положительному направлению Ох. Отсюда k=-13<0, тогда необходимо применить формулу α=π-arctgkПри подстановке получим выражение:
α=π-arctg-13=π-arctg 13=π-π6=5π6.
Ответ: 5π6.
Уравнение с угловым коэффициентом
Уравнение вида y=k·x+b, где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом.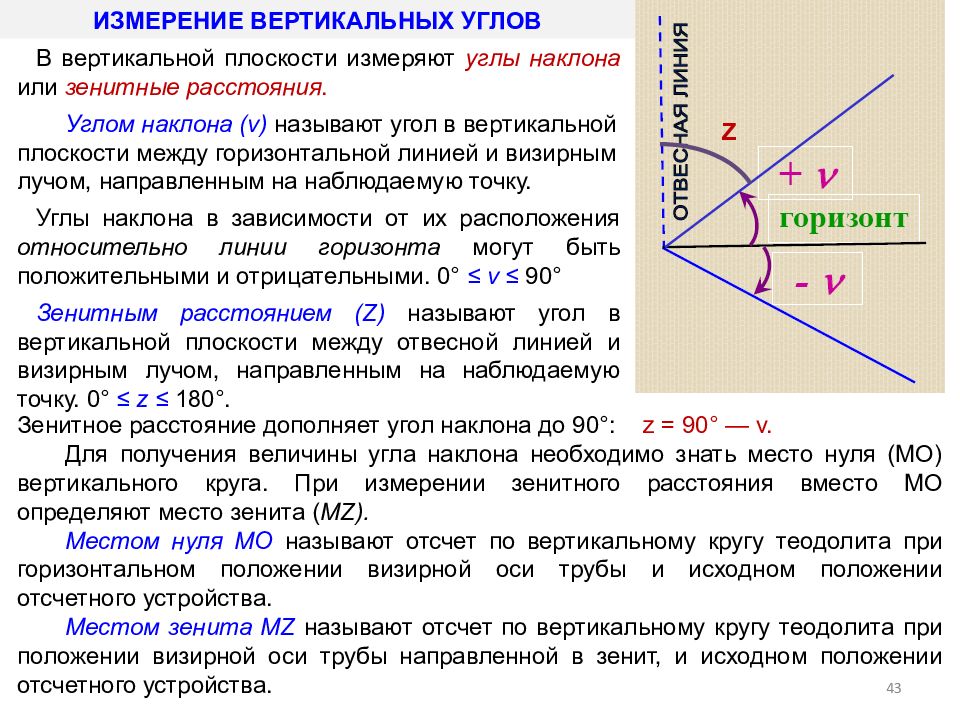 Уравнение характерно для любой прямой, непараллельной оси Оу.
Уравнение характерно для любой прямой, непараллельной оси Оу.
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y=k·x+b. В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М, M1(x1, y1), в уравнениеy=k·x+b, тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Пример 4
Задана прямая с угловым коэффициентом y=13x-1. Вычислить, принадлежат ли точки M1(3, 0) и M2(2, -2) заданной прямой.
Решение
Необходимо подставить координаты точки M1(3, 0) в заданное уравнение, тогда получим 0=13·3-1⇔0=0. Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M2(2, -2), тогда получим неверное равенство вида -2=13·2-1⇔-2=-13. Можно сделать вывод, что точка М2 не принадлежит прямой.
Ответ: М1 принадлежит прямой, а М2 нет.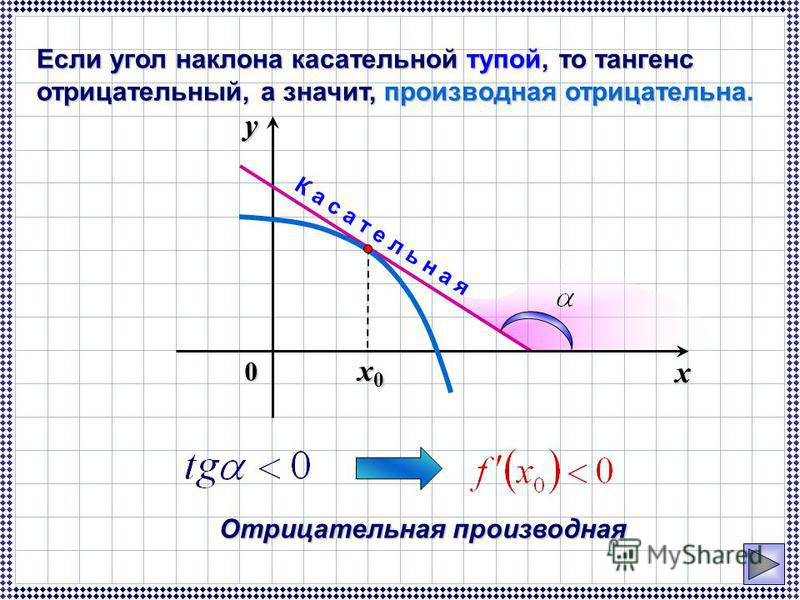
Известно, что прямая определена уравнением y=k·x+b, проходящим через M1(0, b), при подстановке получили равенство вида b=k·0+b⇔b=b. Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y=k·x+b на плоскости определяет прямую, которая проходит через точку 0, b. Она образует угол αс положительным направлением оси Ох, где k=tg α.
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y=3·x-1. Получим, что прямая пройдет через точку с координатой 0, -1 с наклоном в α=arctg3=π3 радиан по положительному направлению оси Ох. Отсюда видно, что коэффициент равен 3.
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M1(x1, y1).
Равенство y1=k·x+b можно считать справедливым, так как прямая проходит через точку M1(x1, y1). Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом.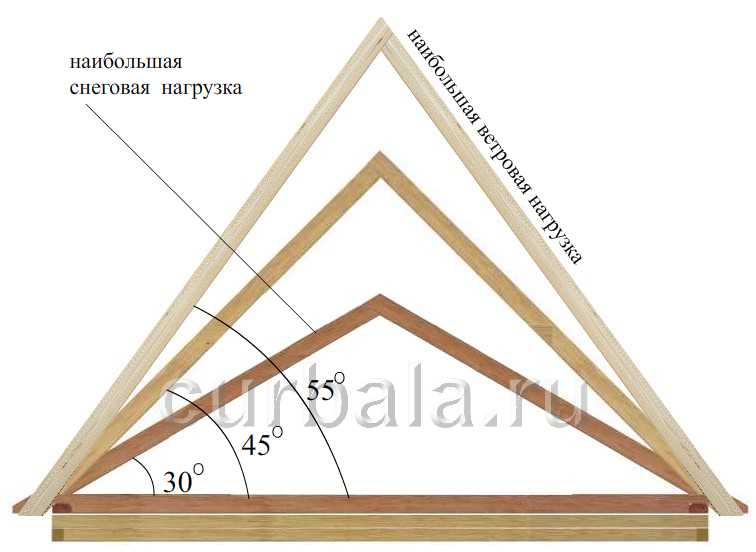 Из этого следует, что y-y1=k·(x-x1). Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M1(x1, y1).
Из этого следует, что y-y1=k·(x-x1). Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M1(x1, y1).
Пример 5
Составьте уравнение прямой, проходящей через точку М1 с координатами (4,-1), с угловым коэффициентом равным -2.
Решение
По условию имеем, что x1=4, y1=-1, k=-2. Отсюда уравнение прямой запишется таким образом y-y1=k·(x-x1)⇔y-(-1)=-2·(x-4)⇔y=-2x+7.
Ответ: y=-2x+7.
Пример 6
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М1 с координатами (3,5), параллельную прямой y=2x-2.
Решение
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y=2x-2, отсюда следует, что k=2. Составляем уравнение с угловым коэффициентом и получаем:
y-y1=k·(x-x1)⇔y-5=2·(x-3)⇔y=2x-1
Ответ: y=2x-1.
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y=k·x+b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x-x1ax=y-y1ay. Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y=k·x+b⇔y-b=k·x⇔k·xk=y-bk⇔x1=y-bk.
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Пример 7
Привести уравнение прямой с угловым коэффициентом y=-3x+12к каноническому виду.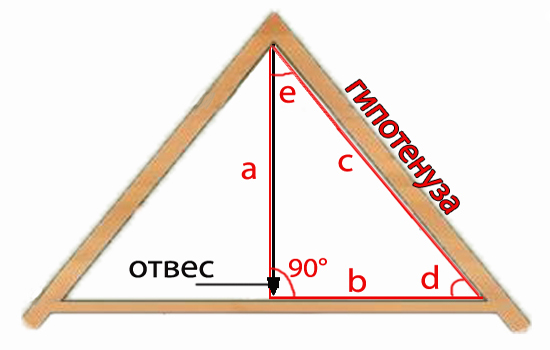
Решение
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y=-3x+12⇔-3x=y-12⇔-3x-3=y-12-3⇔x1=y-12-3
Ответ: x1=y-12-3.
Общее уравнение прямой проще всего получить из y=k·x+b, но для этого необходимо произвести преобразования: y=k·x+b⇔k·x-y+b=0. Производится переход из общего уравнения прямой к уравнениям другого вида.
Пример 8
Дано уравнение прямой видаy=17x-2. Выяснить, является ли вектор с координатами a→=(-1, 7) нормальным вектором прямой?
Решение
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y=17x-2⇔17x-y-2=0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n→=17, -1, отсюда 17x-y-2=0. Понятно, что вектор a→=(-1, 7) коллинеарен вектору n→=17, -1, так как имеем справедливое соотношение a→=-7·n→. Отсюда следует, что исходный вектор a→=-1, 7 — нормальный вектор прямой 17x-y-2=0, значит, считается нормальным вектором для прямой y=17x-2.
Ответ: Является
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения Ax+By+C=0, где B≠0, к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим Ax+By+C=0⇔-AB·x-CB.
Результат и является уравннием с угловым коэффициентом, который равняется -AB.
Пример 9
Задано уравнение прямой вида 23x-4y+1=0 . Получить уравнение данной прямой с угловым коэффициентом.
Решение
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
23x-4y+1=0⇔4y=23x+1⇔y=14·23x+1⇔y=16x+14.
Ответ: y=16x+14.
Аналогичным образом решается уравнение вида xa+yb=1, которое называют уравнение прямой в отрезках, или каноническое вида x-x1ax=y-y1ay. Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
xa+yb=1⇔yb=1-xa⇔y=-ba·x+b.
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔⇔ax·y=ay·x-ay·x1+ax·y1⇔y=ayax·x-ayax·x1+y1
Пример 10
Имеется прямая, заданная уравнением x2+y-3=1. Привести к виду уравнения с угловым коэффициентом.
Привести к виду уравнения с угловым коэффициентом.
Решение.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на -3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y-3=1-x2⇔-3·y-3=-3·1-x2⇔y=32x-3.
Ответ: y=32x-3.
Пример 11
Уравнение прямой вида x-22=y+15 привести к виду с угловым коэффициентом.
Решение
Необходимо выражение x-22=y+15 вычислить как пропорцию. Получим, что 5·(x-2)=2·(y+1). Теперь необходимо полностью его разрешить, для этого:
5·(x-2)=2·(y+1)⇔5x-10=2y+2⇔2y=5x-12⇔y=52x
Ответ: y=52x-6.
Для решения таких заданий следует приводит параметрические уравнения прямой вида x=x1+ax·λy=y1+ay·λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Пример 12
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x=λy=-1+2·λ.
Решение
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x=λy=-1+2·λ⇔λ=xλ=y+12⇔x1=y+12.
Теперь необходимо разрешить данное равенство относительно y, чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x1=y+12⇔2·x=1·(y+1)⇔y=2x-1
Отсюда следует, что угловой коэффициент прямой равен 2. Это записывается как k=2.
Ответ: k=2.
Как рассчитать угол зная длину и высоту. Как рассчитать угол наклона крыши
При проектировании стропил кровли частного дома нужно уметь правильно рассчитать угол наклона крыши. Как сориентироваться в различных единицах измерения, по каким формулам вести расчёт и как влияет угол наклона на ветровую и снеговую нагрузку крыши, мы и поговорим в этой статье.
Кровля частного дома, возводимого по индивидуальному проекту, может быть очень простой или удивительно причудливой. Угол уклона каждого ската зависит от архитектурного решения всего дома, наличия чердака или мансарды, используемого кровельного материала, климатической зоны, в которой располагается приусадебный участок. В компромиссе этих параметров нужно найти оптимальное решение, сочетающее прочность крыши с полезным использованием подкрышного пространства и внешним видом дома или комплекса построек.
Угол уклона каждого ската зависит от архитектурного решения всего дома, наличия чердака или мансарды, используемого кровельного материала, климатической зоны, в которой располагается приусадебный участок. В компромиссе этих параметров нужно найти оптимальное решение, сочетающее прочность крыши с полезным использованием подкрышного пространства и внешним видом дома или комплекса построек.
Единицы измерения угла наклона крыши
Угол наклона — это величина между горизонтальной частью конструкции, плитами или балками перекрытия, и поверхностью кровли или стропилами.
В справочниках, СНиП, технической литературе встречаются различные единицы измерения углов:
- градусы;
- соотношение сторон;
- проценты.
Ещё одна единица измерения углов — радиан — в таких расчётах не применяется.
Что такое градусы, все помнят из школьной программы. Соотношение сторон прямоугольного треугольника, который образован основанием — L, высотой — Н (см. на рисунок выше) и настилом крыши выражается, как Н:L. Если α = 45°, треугольник — равносторонний, и соотношение сторон (катетов) равно 1:1. В случае, когда соотношение не даёт чёткого представления о наклоне, говорят о проценте. Это то же отношение, но рассчитанное в долях с переводом в проценты. Например, при H = 2,25 м и L = 5,60 м:
на рисунок выше) и настилом крыши выражается, как Н:L. Если α = 45°, треугольник — равносторонний, и соотношение сторон (катетов) равно 1:1. В случае, когда соотношение не даёт чёткого представления о наклоне, говорят о проценте. Это то же отношение, но рассчитанное в долях с переводом в проценты. Например, при H = 2,25 м и L = 5,60 м:
- 2,25 м / 5,60 м · 100 % = 40%
Цифровое выражение одних единиц через другие наглядно изображено на диаграмме ниже:
Формулы для расчёта угла наклона крыши, длины стропил и площади покрытия кровельным материалом
Чтобы легко рассчитать размеры элементов крыши и стропильной системы , нужно вспомнить, как мы решали задачи с треугольниками в школе, пользуясь основными тригонометрическими функциями.
Как это поможет в расчёте крыши? Разбиваем сложные элементы на простые прямоугольные треугольники и находим решение для каждого случая, пользуясь тригонометрическими функциями и теоремой Пифагора.
Чаще встречаются более сложные конфигурации.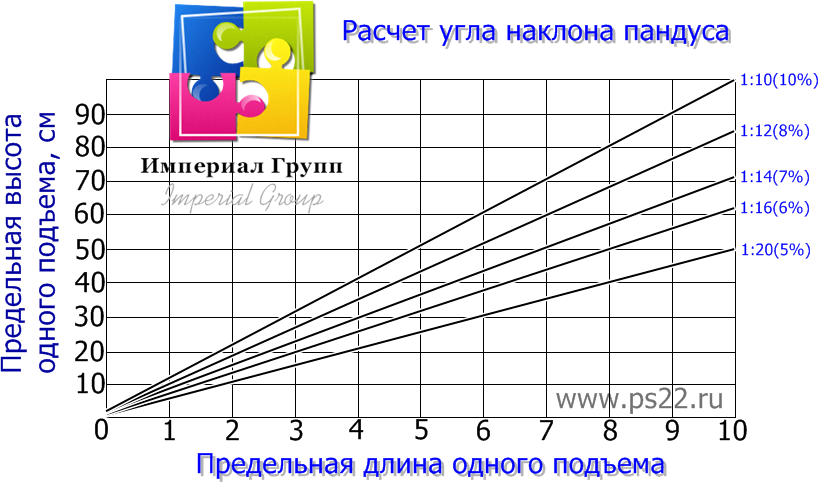
Например, нужно рассчитать длину стропил торцевой части вальмовой крыши, которая представляет собой равнобедренный треугольник. Из вершины треугольника опускаем перпендикуляр на основание и получаем прямоугольный треугольник, гипотенуза которого является средней линией торцевой части крыши. Зная ширину пролёта и высоту конька, из разбитой на элементарные треугольники конструкции можно найти угол наклона вальмы — α, угол наклона кровли — β и получить длину стропил треугольного и трапециевидного ската.
Формулы для расчёта (единицы измерения длин должны быть одинаковыми — м, см или мм — во всех расчётах, чтобы избежать путаницы):
Внимание! Расчёт длин стропил по этим формулам не учитывает величину свеса.
Пример
Крыша — четырёхскатная, вальмовая. Высота конька (СМ) — 2,25 м, ширина пролёта (W/2) — 7,0 м, глубина наклона торцевой части крыши (MN) — 1,5 м.
Получив значения sin(α) и tg(β), определить значение углов можно по таблице Брадиса. Полная и точная таблица с точностью до минуты представляет собой целую брошюру, а для грубых расчётов, которые в данном случае допустимы, можете воспользоваться небольшой таблицей значений.
Полная и точная таблица с точностью до минуты представляет собой целую брошюру, а для грубых расчётов, которые в данном случае допустимы, можете воспользоваться небольшой таблицей значений.
Таблица 1
| Угол наклона крыши, в градусах | tg(a) | sin(a) |
| 5 | 0,09 | 0,09 |
| 10 | 0,18 | 0,17 |
| 15 | 0,27 | 0,26 |
| 20 | 0,36 | 0,34 |
| 25 | 0,47 | 0,42 |
| 30 | 0,58 | 0,50 |
| 35 | 0,70 | 0,57 |
| 40 | 0,84 | 0,64 |
| 45 | 1,00 | 0,71 |
| 50 | 1,19 | 0,77 |
| 55 | 1,43 | 0,82 |
| 60 | 1,73 | 0,87 |
| 65 | 2,14 | 0,91 |
| 70 | 2,75 | 0,94 |
| 75 | 3,73 | 0,96 |
| 80 | 5,67 | 0,98 |
| 85 | 11,43 | 0,99 |
| 90 | ∞ | 1 |
Для нашего примера:
- sin(α) = 0,832, α = 56,2° (получено интерполяцией соседних значений для углов в 55° и 60°)
- tg(β) = 0,643, β = 32,6°(получено интерполяцией соседних значений для углов в 30° и 35°)
Запомним эти цифры, они пригодятся нам при выборе материала.
Для расчёта количества кровельного материала потребуется определить площадь покрытия. Площадь ската двускатной крыши — прямоугольник. Его площадь — произведение сторон. Для нашего примера — вальмовой крыши — это сводится к определению площадей треугольника и трапеции.
Для нашего примера площадь одного торцового треугольного ската при CN = 2,704 м и W/2 = 7,0 м (расчёт необходимо выполнить с учётом удлинения кровли за пределы стен, принимаем длину свеса — 0,5 м):
- S = ((2,704 + 0,5) · (7,5 + 2 х 0,5)) / 2 = 13,62 м 2
Площадь одного бокового трапециевидного ската при W = 12,0 м, H с = 3,905 м (высота трапеции) и MN = 1,5 м:
- L к = W — 2 · MN = 9 м
Вычисляем площадь с учётом свесов:
- S = (3,905 + 0,5) · ((12,0 + 2 х 0,5) + 9,0) / 2 = 48,56 м 2
Суммарная площадь покрытия четырёх скатов:
- S Σ = (13,62 + 48,46) · 2 = 124,16 м 2
Рекомендации по наклону крыши в зависимости от назначения и материала
Неэксплуатируемая крыша может иметь минимальный угол наклона 2-7°, что обеспечивает невосприимчивость к ветровым нагрузкам.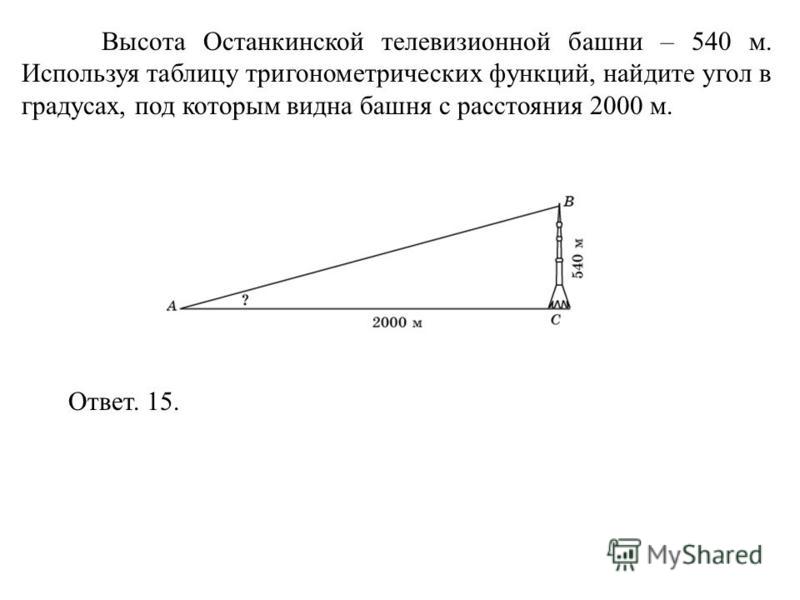 Для нормального схода снега угол лучше увеличить до 10°. Такие кровли распространены при строительстве хозяйственных построек, гаражей.
Для нормального схода снега угол лучше увеличить до 10°. Такие кровли распространены при строительстве хозяйственных построек, гаражей.
Если подкрышное пространство предполагается использовать в качестве чердака или мансарды , наклон одно- или двускатной крыши должен быть достаточно большим, иначе человек не сможет выпрямиться, а полезная площадь будет «съедена» стропильной системой. Поэтому целесообразно применить в таком случае ломаную крышу, например, мансардного типа. Минимальная высота потолков в таком помещении должна быть не менее 2,0 м, но желательно для комфортного пребывания — 2,5 м.
Варианты обустройства мансарды: 1-2. Двухскатная крыша классическая. 3. Крыша с переменным углом наклона. 4. Крыша с выносными консолями
Принимая тот или иной материал в качестве кровельного, необходимо учитывать требования по минимальному и максимальному уклону. В противном случае, возможны проблемы, требующие ремонта крыши или всего дома.
Таблица 2
| Тип кровли | Диапазон допустимых углов монтажа, в градусах | Оптимальный наклон кровли, в градусах |
| Кровля из толя с посыпкой | 3-30 | 4-10 |
| Толевая кровля, двухслойная | 4-50 | 6-12 |
| Цинковая кровля с двойными стоячими фальцами (из цинковых лент) | 3-90 | 5-30 |
| Толевая кровля, простая | 8-15 | 10-12 |
| Пологая кровля, крытая кровельной сталью | 12-18 | 15 |
| Шпунтованная черепица с 4-мя желобками | 18-50 | 22-45 |
| Гонтовая кровля | 18-21 | 19-20 |
| Шпунтованная черепица, нормальная | 20-33 | 22 |
| Профнастил | 18-35 | 25 |
| Волнистый асбестоцементный лист | 5-90 | 30 |
| Искусственный шифер | 20-90 | 25-45 |
| Шиферная кровля, двухслойная | 25-90 | 30-50 |
| Шиферная кровля, нормальная | 30-90 | 45 |
| Стеклянная кровля | 30-45 | 33 |
| Черепица, двухслойная | 35-60 | 45 |
| Желобчатая голландская черепица | 40-60 | 45 |
Полученные в нашем примере углы наклона находятся в диапазоне 32-56°, что соответствует шиферной кровле, но не исключает и некоторые другие материалы.
Определение динамических нагрузок в зависимости от угла наклона
Конструкция дома должна выдерживать статические и динамические нагрузки от крыши. Статические нагрузки — это вес стропильной системы и кровельных материалов, а также оборудования подкрышного пространства. Это постоянная величина.
Динамические нагрузки — величины переменные, зависящие от климата и времени года. Чтобы верно рассчитать нагрузки с учётом их возможной сочетаемости (одновременности), рекомендуем изучить СП 20.13330.2011 (разделы 10, 11 и Приложение Ж). В полном объёме этот расчёт с учётом всех возможных при конкретном строительстве факторах в этой статье не может быть изложен.
Ветровая нагрузка вычисляется с учётом районирования, а также особенностей расположения (подветренная, наветренная сторона) и угла наклона крыши, высоты здания. Основу расчёта составляет ветровое давление, средние значения которого зависит от региона строящегося дома. Остальные данные нужны для определения коэффициентов, корректирующих относительно постоянную для климатического района величину. Чем больше угол наклона, тем более серьёзные ветровые нагрузки испытывает крыша.
Чем больше угол наклона, тем более серьёзные ветровые нагрузки испытывает крыша.
Таблица 3
Снеговая нагрузка, в отличие от ветровой, связана с углом наклона крыши противоположным образом: чем меньше угол, тем больше снега задерживается на кровле, тем ниже вероятность схождения снежного покрова без применения дополнительных средств , и тем большие нагрузки испытывает конструкция.
Таблица 4
Подходите к вопросу определения нагрузок серьёзно. Расчёт сечений, конструкции, а значит, надёжности и стоимости стропильной системы зависит от полученных значений. Если вы не уверены в своих силах, лучше заказать расчёт нагрузок у специалистов.
1.
2.
3.
4.
5.
Процесс возведения крыши может остановиться, если заранее не подумать о таких вещах как угол наклона кровли и используемый кровельный материал. Так как эти два показателя имеют прямое влияние друг на друга, то их обязательно стоит учитывать наравне. Напомним, что кровли могут иметь один, два или четыре ската. В зависимости от типа, необходимо правильно подобрать углы скатов и материалы. В данной статье речь будет идти как раз о том, как рассчитать угол наклона крыши.
В зависимости от типа, необходимо правильно подобрать углы скатов и материалы. В данной статье речь будет идти как раз о том, как рассчитать угол наклона крыши.
Что влияет на угол ската крыши?
Точный угол зависит от ряда факторов:
- выбранного материала кровли;
- климатических особенностей региона;
- целевого назначения здания.
В случае двухскатной крыши и более сложной конструкции, на выбор угла влияет не только особенности климата, но также и цели использования чердака. Так, например, если он будет нежилым, то есть используется для хранения различных вещей, то не нужно организовывать большую высоту подкровельного помещения. Ну а если под крышей будет полноценная мансарда, то здесь не обойтись без высокой крыши с большими углами наклонов.
Но на что в итоге следует обратить внимание? На дизайнерское решение, то есть на проект здания, на выбранный материал кровли, на количество осадков и силу ветров.
Очевидно, что для регионов с сильными ветрами необходимо возводить крышу с малыми углами — это позволяет снизить нагрузки на стропильную систему, а также избежать неприятного эффекта «срывания» кровли. Такая же конструкция крыши пригодится и для домов, возведенных в солнечных регионах с высокой температурой воздуха и малым количеством осадков. Для регионов с выраженными атмосферными явлениями (дожди, град, снегопады) угол наклона кровли должен быть большим — вплоть до 60 градусов. Это позволяет разгрузить крышу и стропила от нагрузки снега и воды. Кроме того, благодаря быстрому удалению осадков с поверхности, снижается вероятность протекания кровельного материала в местах стыков.
Такая же конструкция крыши пригодится и для домов, возведенных в солнечных регионах с высокой температурой воздуха и малым количеством осадков. Для регионов с выраженными атмосферными явлениями (дожди, град, снегопады) угол наклона кровли должен быть большим — вплоть до 60 градусов. Это позволяет разгрузить крышу и стропила от нагрузки снега и воды. Кроме того, благодаря быстрому удалению осадков с поверхности, снижается вероятность протекания кровельного материала в местах стыков.
Для того, чтобы рассчитать угол наклона крыши необходимо принимать во внимание все вышесказанное. Как правило, оптимальными считаются углы наклона скатов в пределах 20-45 градусов. Перед тем, стоит учитывать ширину стены, то есть расстояние от начала скатов, так как при увеличении этого значения можно значительно снизить угол, при этом не ограничив чердак в высоте.
Кровля из металлочерепицы
Хорошо известно, что металлочерепица гораздо тяжелее других материалов. Именно поэтому стоит очень внимательно проводить расчеты несущей способности системы стропил.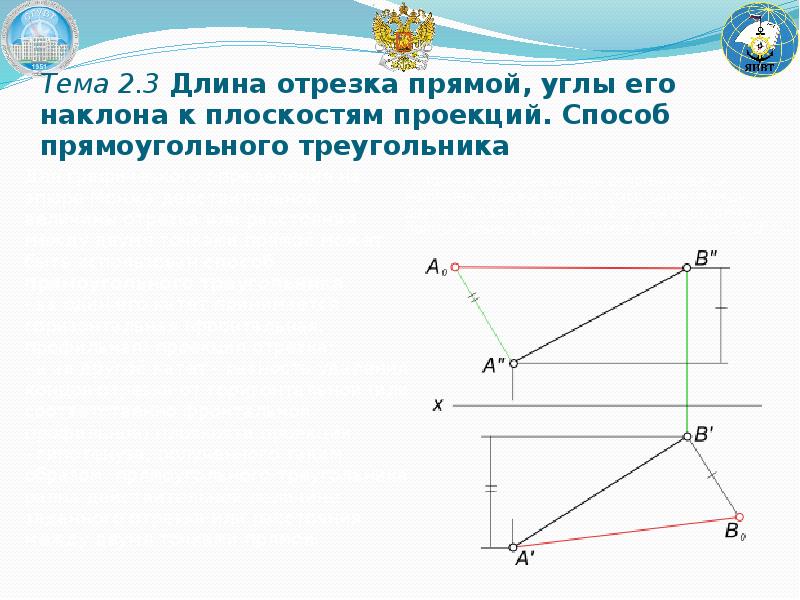 Особенно важно учитывать вес материала и в регионах с сильными ветрами. Динамические нагрузки оказывают крайне негативное влияние на материал и несущую конструкцию, особенно сильно это проявляется при больших углах наклона крыши.
Особенно важно учитывать вес материала и в регионах с сильными ветрами. Динамические нагрузки оказывают крайне негативное влияние на материал и несущую конструкцию, особенно сильно это проявляется при больших углах наклона крыши.
Для кровель, возводимых с использованием металлочерепицы, среднее значение угла наклона составляет 22 градуса. Согласно наблюдениям профессионалов именно такой уклон позволяет предотвратить скапливание и проникновение влаги на стыках, хорошо отводить снег и воду, а также противостоять нагрузкам ветра. при этом должен составлять не менее 14 градусов. Для мягкой черепицы этот показатель равен 11 градусам, при этом такая кровля требует организации сплошной обрешетки.
Кровля из профнастила
Данный материал пользуется огромной популярностью. Он отличается малым весом, простотой установки и ремонта. Кроме того, закрепить листы профнастила на обрешетке очень просто. Минимальный угол такой кровли составляет 12 градусов. Именно эта рекомендация указана в инструкции большинства производителей материала.
Кровля из рулонных «мягких» материалов
К таким материалам относят ондулин, рубероид, мембранные покрытия. В зависимости от количества слоев, используемых для покрытия крыши, угол наклона может колебаться от 2 до 15 градусов. Так, для двухслойной кровли уклон составляет 15 градусов, в то время как трехслойная конструкция позволяет покрывать плоскую крышу с углом наклона 2-5 градусов.
Мембранные покрытия могут использоваться для возведения крыш абсолютно любой конфигурации независимо от ее сложности. Так, угол наклона четырехскатной крыши (отдельных ее элементов) может составлять от 2 градусов.
Как можно понять из всего сказанного выше, выбранный угол наклона зависит от решения хозяина. Но при этом во внимание принимаются нагрузки на несущую конструкцию (статические и динамические). Также важно учесть тип обрешетки и ее шаг, так как эти параметры зависят именно от угла наклона. Для малых углов шаг обрешетки составляет в среднем 35-45 см.
Угол наклона крыши напрямую влияет и на расход кровельного материала.
Так, чем больший угол, тем больше потребуется материала для покрытия плоскостей.
Во время подбора кровельного материала можно воспользоваться следующими советами:
- при малом уклоне кровли (до 10 градусов), крышу можно покрыть с использованием гравия и крошки камня. При этом берут слой гравия равный 15 мм, а крошки камня — 5 мм;
- при более выраженных углах наклона крыши обязательно применяют гидроизоляцию с помощью битума. Для рулонных материалов, кроме всего прочего, необходимо провести покрытие защитным материалом;
- асбестоцементные листы и профнастил требуют обязательной герметизации швов. Все стыки при этом делаются двойными.
Проекты возводимых загородных особняков могут учитывать множество требований, пожеланий и даже причуд или «капризов» их владельцев владельца. Но всегда их «роднит» общая особенность — без надежной крыши никогда не обходится ни одно их зданий. И в этом вопросе на первый план должны выходить не столько архитектурные изыски заказчика, сколько специфические требования к этому элементу строения. Это надежность и устойчивость всей стропильной системы и кровельного покрытия, полноценное выполнение крышей своего прямого предназначения — защиты от проникновения влаги (а в ряде случаев, кроме того, еще и термо- и звукоизоляции), при необходимости — функциональность расположенных непосредственно под кровлей помещений.
Это надежность и устойчивость всей стропильной системы и кровельного покрытия, полноценное выполнение крышей своего прямого предназначения — защиты от проникновения влаги (а в ряде случаев, кроме того, еще и термо- и звукоизоляции), при необходимости — функциональность расположенных непосредственно под кровлей помещений.
Проектирование конструкции крыши — дело чрезвычайно ответственное и достаточно непростое, особенно при сложных ее конфигурациях. Разумнее всего будет доверить это дело профессионалам, которое владеют методикой проведения необходимых расчетов и соответствующим программным обеспечение для этого. Однако, владельцу дома тоже могут быть интересны некоторые теоретические моменты. Например, немаловажно знать, как рассчитать угол наклона крыши самостоятельно, хотя бы приблизительно — для начала. Это даст возможность сразу прикинуть возможность реализации своих «авторских прикидок» — по соответствию задуманного реальным условиям региона, по «архитектуре» самой крыши, по планируемому кровельному материалу, по использованию чердачного помещения. В определенной степени рассчитанный угол ската кровли поможет провести предварительный подсчет параметров и количества пиломатериалов для стропильной системы, общей площади кровельного покрытия.
В определенной степени рассчитанный угол ската кровли поможет провести предварительный подсчет параметров и количества пиломатериалов для стропильной системы, общей площади кровельного покрытия.
В каких величинах удобнее измерять угол ската крыши?
Казалось бы — совершенно излишний вопрос, так как все со школьной скамьи знают, что угол измеряется в градусах. Но ясность здесь все же нужна, потому что и в технической литературе, и в справочных таблицах, и в привычном обиходе некоторых опытных мастеров нередко встречаются и иные единицы измерения — проценты или же относительные соотношения сторон.
И еще одно необходимое уточнение — что принимается за угол наклона крыши?
Угол наклона — это угол, образованный пересечением двух плоскостей: горизонтальной и плоскостью ската кровли. На рисунке он показан буквой греческого алфавита α.
Интересующие нас острые углы (тупоугольных скатов не может быть просто по определению), лежит в диапазоне от 0 до 90°.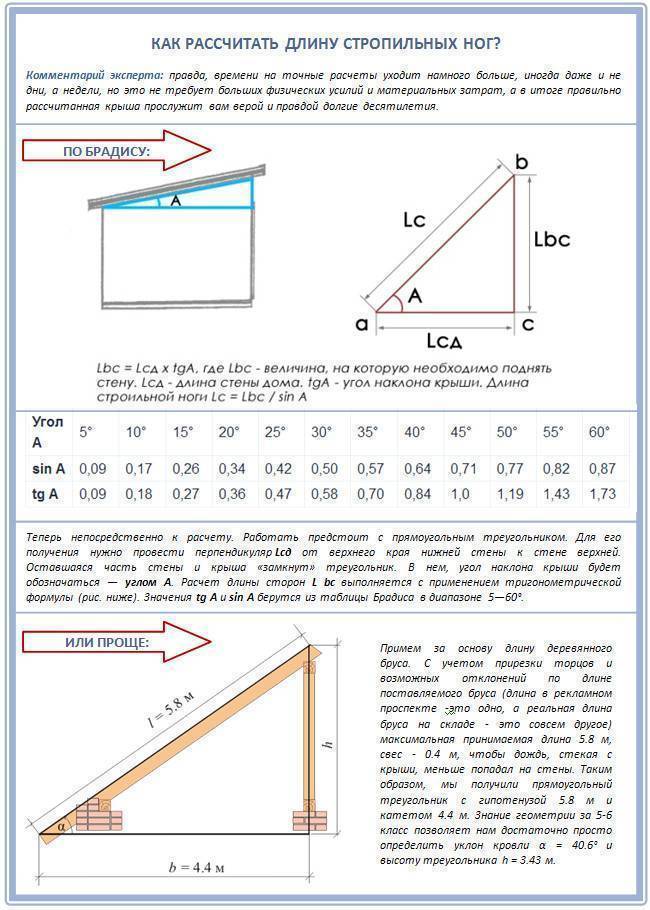 Скаты круче 50 ÷ 60 ° в «чистом» виде встречаются чрезвычайно редко и то, как правило, для декоративного оформления крыш — при строительстве остроконечных башенок в готическом стиле. Однако есть и исключение — такими крутыми могут быть скаты нижнего ряда стропил крыши мансардного типа.
Скаты круче 50 ÷ 60 ° в «чистом» виде встречаются чрезвычайно редко и то, как правило, для декоративного оформления крыш — при строительстве остроконечных башенок в готическом стиле. Однако есть и исключение — такими крутыми могут быть скаты нижнего ряда стропил крыши мансардного типа.
И все же чаще всего приходится иметь дело со скатами, лежащим в диапазоне от 0 до 45°
С градусами понятно — все, наверное, представляют транспортир с его делениями. А ка быть с другими единицами измерения?
Тоже ничего сложного.
Относительное соотношение сторон — это максимально упрощенная дробь, показывающая отношение высоты подъёма ската (на рисунке выше обозначена латинской Н) к проекции ската крыши на горизонтальную плоскость (на схеме — L).
L — это может быть, в зависимости от конструкции крыши, половина пролета (при симметричной двускатной крыше), пролет полностью (если крыша односкатная), либо, при сложных конфигурациях кровли, действительно линейный участок, определяемый проведенной к горизонтальной плоскости проекцией. Например, на схеме мансардной крыши такой участок хорошо показан — по горизонтальной балке от самого угла до вертикальной стойки, проходящей от верхней точки нижнего стропила.
Например, на схеме мансардной крыши такой участок хорошо показан — по горизонтальной балке от самого угла до вертикальной стойки, проходящей от верхней точки нижнего стропила.
Угол уклона так и записывается, дробью, например «1: 3».
Однако, на практике нередко случается так, что использовать величину угла уклона в таком представлении будет чрезвычайно неудобен, если, скажем, числа в дроби получаются некруглые и несокращаемые. Например, мало что скажет неопытному строителю соотношение 3: 11. На этот случай есть возможность воспользоваться еще одной величиной измерения уклона крыши — процентами.
Находится эта величина чрезвычайно просто — необходимо просто найти результат деления уже упомянутой дроби, а затем умножить его на 100. Например, в приведенном выше примере 3: 11
3: 11 = 0,2727 × 100 = 27,27 %
Итак, получена величина уклона ската кровли, выраженная в процентах.
А что делать, если требуется перейти от градусов к процентам или наоборот?
Можно запомнить такое соотношение.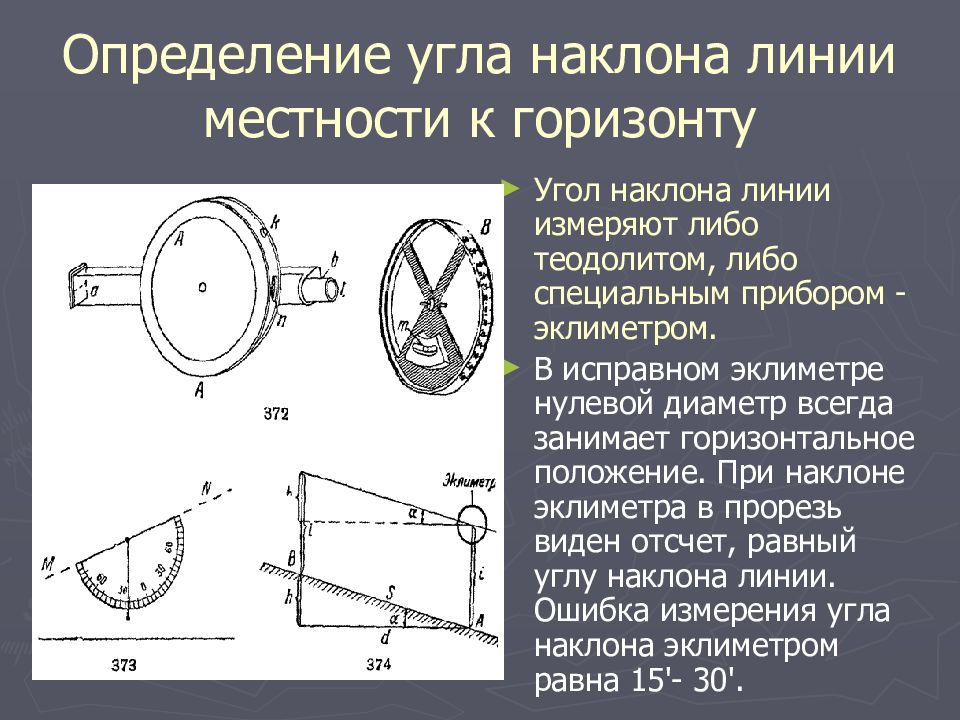 100 % — это угол 45 градусов, когда катеты прямоугольного треугольника равны между собой, то есть в нашем случае высота ската равна длине его горизонтальной проекции.
100 % — это угол 45 градусов, когда катеты прямоугольного треугольника равны между собой, то есть в нашем случае высота ската равна длине его горизонтальной проекции.
В таком случае, 45° / 100 = 0,45° = 27´. Один процент уклона равен 27 угловым минутам.
Если подойти с другой стороны, то 100 / 45° = 2,22 %. То есть получаем, что один градус — это 2, 22% уклона.
Для простоты перевода величин из одних в другие можно воспользоваться таблицей:
Для наглядности будет полезным привести графическую схему, которая очень доступно показывает взаимосвязь всех упомянутых линейных параметров с углом ската и величинами его измерения.
К этому рисунку еще предстоит вернуться, когда будут рассматриваться виды кровельных покрытий.
Зависимость типа кровельного покрытия от крутизны ската
Планируя постройку собственного дома, хозяин участка наверняка уже проводит «прикидку» и своей голове, и с членами семьи — как будет выглядеть их будущее жилье. Кровля в этом вопросе, безусловно, занимает одно из первостепенных значений. И вот здесь необходимо учитывать то, что далеко не всякий кровельный материал может использоваться на различных по крутизне скатах крыш. Чтобы не возникало недоразумений позднее, необходим заранее предусматривать эту взаимосвязь.
Крыши по углу наклона ската можно условно разделит на плоские (уклон до 5°), с малым уклоном (от 6 до 30°) и крутоуклонные, соответственно, с углом ската более 30°.
У каждого из типов крыш есть свои достоинства и недостатки. Например, плоские крыши имеют минимальную площадь, но потребуют особых мер гидроизоляции. На крутых крышах не задерживаются снежные массы, однако они больше подвержены ветровой нагрузке из-за своей «парусности». Так и кровельный материал — в силу собственных технологических или эксплуатационных особенностей имеет определенные ограничения на применения с разными уклонами скатов.
Обратимся к уже рассматриваемому ранее рисунку (схема A). Черными кружками с дугообразными стрелками и синими цифрами обозначены области применения различных кровельных покрытий (острие стрелки указывает на минимально допустимое значение крутизны ската):
1 — это дранка, щепа, натуральный гонт. В этой же области лежит и применение до сих пор используемых в южных краях камышовых кровель.
2 — натуральное штучное черепичное покрытие, битумно-полимерные плитки, сланцевые плитки.
3 — рулонные материалы на битумной основе, не менее четырёх слоев, с внешней гравийной посыпкой, утопленной в слой расплавленной мастики.
4 — аналогично пункту 3, но для надёжности кровли достаточно трех слоев рулонного материала.
5 — аналогичные вышеописанным рулонные материалы (не менее трех слоев), но без наружной защитной гравийной посыпки.
6 — рулонные кровельные материалы, наклеиваемые на горячую мастику не менее, чем в два слоя. Металлочерепица, профнастил.
7 — волнистые асбестоцементные листы (шифер) унифицированного профиля.
8 — черепичное глиняное покрытие.
9 — асбестоцементные листы усиленного профиля.
10 — кровельная листовая сталь с развальцовкой соединений.
11 — шиферное покрытие обычного профиля.
Таким образом, если есть желание покрыть крышу кровельным материалом определенного типа, угол уклона ската должен планироваться в указанных рамках.
Зависимость высоты конька от угла наклона крыши
Для тех читателей, которые хорошо помнят курс тригонометрии средней школы, этот раздел может показаться неинтересным. Они могут сразу его пропустить и перейти дальше. А вот подзабывшим это нужно освежить знания о взаимозависимости углов и сторон в прямоугольном треугольнике.
Для чего это надо? В рассматриваемом случае возведения крыши всегда в расчетах отталкиваются от прямоугольного треугольника. Два его катета — это длина проекции ската на горизонтальную плоскость (длина пролета, половины пролета и т.п. — в зависимости от типа крыши) и высота ската в высшей точке (на коньке или при переходе на верхние стропила — при расчете нижних стропил мансардной крыши). Понятно, что постоянная величина здесь одна — это длина пролета. А вот высоту можно изменять, варьируя угол наклона крыши.
В таблице приведены две основные зависимости, выраженные через тангенс и синус угла наклона ската. Существуют и иные зависимости (через косинус или котангенс) но в данном случае нам достаточно этих двух тригонометрических функций.
Зная эти тригонометрические тождества, можно решить практически все задачи по предварительному проектированию стропильной конструкции.
Так, если необходимо «плясать» от четко установленной высоты подъёма конька, то отношением tg α = H / L несложно будет определить угол.
По полученному делением числу в таблице тангенсов находят угол в градусах. Тригонометрические функции часто бывают заложены в инженерные калькуляторы, они есть в обязательном порядке в таблицах Exel (для тех, кто умеет работать с этим удобным приложением. Правда, там расчет ведется не в градусах, а в радианах). Но чтобы нашему читателю не приходилось отвлекаться на поиски нужных таблиц, приведем значение тангенсов в диапазоне от 1 до 80°.
В случае, наоборот, когда за основу берется угол наклона кровли, высота расположения конька определяется по обратной формуле:
Теперь, имея значения двух катетов и угла наклона кровли, очень просто вычислить и требуемую длину стропила от конька до карнизного свеса. Можно применить теорему Пифагора
S = √ (L² + H²)
Или же, что, наверное, проще, так как уже известна величина угла, применить тригонометрическую зависимость:
Значение синусов углов — в таблице ниже.
Умелое использование тригонометрических формул позволяет, при нормальном пространственном воображении и при умении выполнять несложные чертежи, провести расчеты и более сложным по конструкции крыш.
Например, даже кажущуюся такой «навороченной» вальмовую или мансардную крышу можно разбить на совокупности треугольников, а затем последовательно просчитать все необходимые размеры.
Зависимость размеров помещения мансарды от угла наклона скатов крыши
Если хозяевами будущего дома планируется использовать чердак в качестве функционального помещения, иначе говоря — сделать мансарду, то определение угла ската крыши приобретает вполне прикладное значение.
Чтобы стало несколько понятнее, лучше выполнить подобную схему в определенном масштабе. Вот, например, как будет выглядеть мансардное помещение в доме с шириной фронтонной части 10 метров. Следует учитывать, что высота потолка никак не может быть ниже 2 метров. (Откровенно говоря, и двух метров маловато для жилого помещения- потолок будет неизбежно «давить» на человека. Обычно исходят из высоты хотя-бы 2.5 метра).
Можно привести уже подсчитанные средние значения получаемой в мансарде комнаты, в зависимости от угла наклона обычной двускатной крыши. кроме того, в таблице приведены величины длины стропил и площади кровельного материала с учетом 0,5 метров карнизного свеса кровли.
Итак, чем круче наклон скатов, тем просторнее помещение. Однако, это сразу отзывается резким увеличением высоты стропильной конструкции, возрастанием размеров, а стало быть — и массы деталей для ее монтажа. Гораздо больше потребуется и кровельного материала — площадь покрытия также быстро растет. Плюс к этому, нельзя забывать и о возрастании эффекта «парусности» — большей подверженности ветровой нагрузке. Видам внешних нагрузок будет посвящена последняя глава настоящей публикации.
Чтобы в определенной степени нивелировать подобные негативные последствия, проектировщики и строители часто применяют особую конструкцию мансардной крыши — о ней уже упоминалось в настоящей статье. Она сложнее в расчетах и изготовлении, но дает существенный выигрыш в получаемой полезной площади мансардного помещения с уменьшением общей высоты здания.
Зависимость величины внешних нагрузок от угла наклона крыши
Еще одно важнейшее прикладное применение рассчитанного значения угла наклона кровли — это определение степени его влияния на уровень внешних нагрузок, выпадающих на конструкцию крыши.
Здесь прослеживается интересная взаимосвязь. Можно заранее рассчитать все параметры — углы и линейные размеры, но всегда в итоге приходят к деталировке. То есть необходимо определить, из какого материала будут изготавливаться детали и узлы стропильной системы, какова должна быть их площадь сечения, шаг расположения, максимальная длина между соседними точками опоры, способы крепления элементов между собой и к несущим стенам здания и многое другое.
Вот здесь на первый план выходят нагрузки, которые испытывает конструкция крыши. Помимо собственного веса, огромное значение имеют внешние воздействия. Если не брать в расчет несвойственные для наших краев сейсмические нагрузки, то главным образом надо сосредоточится на снеговой и ветровой. Величина обеих — напрямую связана с углом расположения кровли к горизонту.
Итак, трудно преуменьшить значение правильного расчета угла наклона крыши, влияние этого параметра на целый ряд важнейших характеристик стропильной системы, да и всего здания в целом. Хотя проведение настоящих архитектурных расчетов, конечно, является в большей мере прерогативой специалистов, умение ориентироваться в основных понятиях и проводить несложные базовые вычисления — будет очень полезным для каждого грамотного владельца дома.
И в завершение статьи — видео-урок по расчету стропильной системы обычной двускатной крыши:
Сложно представить себе любое здание без крыши. Кровля должна защищать здание от воздействия природных осадков, обладать огнестойкими и водонепроницаемыми свойствами, обеспечивать эффективный отвод атмосферных осадков. Долговечность эксплуатации здания и его отдельных элементов во многом зависит от качественной крыши. Для достижения лучших результатов стоит использовать более простые виды скатных крыш: односкатные, двухскатные, вальмовые, полувальмовые, мансардные.
Минимальный угол наклона крыши из металлочерепицы должен составлять 14 градусов.
Основные данные
График выбора кровельного материала в зависимости от уклона крыши.
Допустимый угол наклона металлической крыши обычно измеряют своими руками исходя из климатических условий того района, в котором ведется строительство, и кровельного материала. Минимально угол наклона должен составлять 110°, максимальный угол наклона можно определить путем анализа погодных условий, его значение может быть 45°. и больше. Для более теплого и сухого климата используется менее пологая крыша. Более крутой угол наклона дает возможность минимально скапливать снег и, соответственно, снижать снеговую нагрузку. Например, уклон 45° позволяет почти не учитывать вес снежного покрова.
Наряду с этим, увеличенный угол наклона резко повышает давление ветра на крышу. При уклоне в 45° давление ветра больше в 5 раз по сравнению с показателем в 11°. Следовательно, для большего угла наклона возникает необходимость в большем количестве реек для усиления обрешетки и стропил. От угла уклона крыши прямо зависит и ее стоимость.
Для кровли с углом наклона около 40-45° необходимо больше материалов (примерно в 1,5 раза), нежели для плоской крыши, а для 60° требуется в 2 раза больше кровельных материалов. При выборе конфигурации важно помнить, что от угла наклона напрямую зависит . Учет угла наклона позволяет определить материалы для кровли, а также произвести расчет слоев крыши и ее площади.
Материалы для кровли по своим свойствам (технические, экономические, физические) объединились в группе 1-11.
На графике они показаны дугообразными стрелками. Линии наклона показывают уклон ската. Выделенная (жирным) линия на графике обозначает отношение полной высоты данного конька h к половине его обычного заложения ½. Отношение 1/2 указывает, что вертикальный отрезок h располагается на горизонтальном отрезке ½ два раза. Наклонная линия на полукруглой шкале обозначает угол наклона в градусах, а шкала, расположенная вертикально, — уклон крыши в %.
Так рассчитывают минимальный уклон для тех или иных кровельных материалов. В качестве примера, с помощью данного графика проведем расчет нужного угла наклона для данной крыши с использованием металлической черепицы.
Как измерить уклон
На графике ищем наклонную линию, с которой стыкуется дугообразная стрела 2. Пересечение наклонной линии c вертикальной шкалой определяет уклон, минимально допустимый для данной крыши, который равен 50%. Нам известно, что уклон ската определяется отношением высоты конька к половине его заложения. Произведем расчет таким образом:
i = 10 метров (заложение)
h = 4 метра (высота конька)
получаем
i= h / (1/2) = 4 / (10/2) = 0,8
Для того чтобы измерить уклон в %, это отношение умножают на 100
Таким образом, уклон в 80% при соблюдении норм строительства обеспечит достаточный сброс дождевой воды со всей площади. Для кровли из рулонных полимерно-битумных, битумных и мастичных материалов с уклоном 10° необходим защитный слой для основного водоизоляционного покрова из гравия либо каменной крошки, у которой марка морозостойкости не меньше 100. Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки — 0,3-0,5 см.
Причем на крышах с уклоном примерно до 2,5% с использованием эластомерных пленочных материалов в рулонах, выполненных свободной кладкой, необходим утяжеляющий слой гравия из расчета 50 кгс/кв.м.
На крышах из битумно-полимерных или битумных покрытий в рулонах с углом наклона выше 10% верхний слой гидроизоляционного покрова выполняется из крупнозернистой посыпки. На крышах из мастичных материалов с углом больше 10% предусматривается защитный слой из красочных составов.
При создании крыши из асбестоцементных листов, а также профнастила и металлической черепицы с наклоном до 20% по всей площади необходимо производить герметизацию стыков. Не более чем на 5% можно допустить отклонение из мелкоштучных материалов. Производя эти расчеты, можно узнать площадь помещения мансарды или чердака.
Единицы измерения и инструменты
В основание металлической конструкции встроены цифровой дисплей с элементами управления.
Величина уклона на всех чертежах может обозначаться в градусах или в процентах, а сам он обозначается буквой «i». В настоящий момент нет строгих правил, как обозначать данную величину. Единицей измерения считают градусы или проценты (%).
Угол уклона измеряется двумя способами:
- Специальным уклономером.
- Математическим способом, с помощью вычислений.
Уклономер — это специальная рейка с рамкой, у которой между планками есть ось, на которой закреплен маятник, и своя шкала деления. Когда эта рейка расположена в горизонтальном положении, то маятник на ее шкале отклонен на ноль градусов. Для произведения измерения уклона ската рейку прибора располагают перпендикулярно коньку, в вертикальном положении.
По шкале определяют угол отклонения маятника, который указывает уклон этого ската данной крыши в градусах. Этот метод определения применяется очень и очень редко. На данный момент разработано множество геодезических приборов для определения этих величин и специальные уровни-уклономеры, как капельные, так и электронные.
Математический расчет
- Вертикальная высота (обозначается как H) — высота от верхней точки данного ската (обычно считают от конька) до самой нижней точки (так называемого карниза).
- Заложение — горизонтальный промежуток от самой нижней точки данного ската до самой верхней его точки.
Уклон крыши (его величину) с применением математического расчета находят так.
Угол наклона отдельного ската i выражается через отношение измеренной высоты крыши Н к расстоянию заложения L. Таким образом
Для точного определения этого значения в процентах отношение i умножают на 100. Затем, для определения его значения в градусах, мы производим перевод процентов в градусы.
Для полного понимания этого метода приведем наглядный расчет:
высота равна 3,0 м,
длина заложения равна 5 м.
По формуле вычисляем i:
Проводим расчет процентов
Переводим в градусы. Получаем 31 градус.
Онлайн-калькулятор двускатной крыши поможет вам рассчитать углы наклона стропил, необходимое количество обрешётки, предельную нагрузку на кровлю, а также материалы, необходимые для строительства крыши данного типа при заданных размерах. Вы сможете рассчитать кровлю из таких популярных кровельных материалов, как шифер, ондулин, керамическая, цементно-песчаная и битумная черепица, металлочерепица и других материалов.
При расчётах учитываются параметры, приведенные в ТКП 45-5.05-146-2009 и СНиП «Нагрузки и воздействия».
Двускатная крыша (также известная как двухскатная или щипцовая) – разновидность крыши, имеющая два наклонных ската, которые идут от конька к наружным стенам здания. Это самый распространённый вид крыши на сегодняшний день. Объясняется это её практичностью, малыми затратами на возведение, эффективной защитой помещений и эстетичным внешним видом.
Стропила в конструкции двухскатной крыши опираются друг на друга, соединяясь попарно. С торцевой стороны двускатные крыши имеют форму треугольника, такие торцы называются щипцами или фронтонами. Обычно под такой кровлей устраивается чердак, который освещается с помощью маленьких окон на фронтонах (чердачных окошек).
Вводя в калькулятор данные, непременно сверьтесь с дополнительной информацией, помеченной иконкой.
Внизу этой страницы вы можете оставить отзыв, задать свой собственный вопрос разработчикам или предложить идею по улучшению этого калькулятора.
Разъяснение результатов расчетов
Угол наклона крыши
Под этим углом наклонены стропила и скат крыши. Подразумевается, что планируется строительство симметричной двускатной крыши. Помимо расчета угла, калькулятор проинформирует, насколько угол соответствует нормам по выбранному вами кровельному материалу. Если потребуется изменить угол, то для этого нужно изменить ширину основания или высоту подъёма крыши, либо выбрать другой (более легкий) кровельный материал.
Площадь поверхности крыши
Суммарная площадь кровли (включая свесы заданной длины). Определяет количество кровельных и изоляционных материалов, которые понадобятся для работ.
Примерный вес кровельного материала
Суммарный вес кровельного материала, необходимого для полного покрытия площади крыши.
Количество рулонов изоляционного материала с нахлестом
Общее количество изоляционного материала в рулонах, которое потребуется для изоляции кровли. В расчетах за основу берутся рулоны длиной 15 метров и шириной 1 метр.
Максимальная нагрузка, приходящаяся на стропильную систему. В расчетах учитывается вес всей кровельной системы, форма крыши, а также ветровые и снеговые нагрузки указанного вами региона.
Длина стропил
Полная длина стропил от начала ската до конька крыши.
Количество стропил
Суммарное количество стропил, требуемых для строительства крыши с заданным шагом.
Минимальное сечение стропил, Вес и Объем бруса для стропил
В таблице представлены рекомендуемые размеры сечений стропил (по ГОСТ 24454-80 Пиломатериалы хвойных пород). Для определения соответствия во внимание берется тип кровельного материала, площадь и форма конструкции крыши, а также оказываемые на кровлю нагрузки. В соседних столбцах отображается общий вес и объем этих стропил для всей крыши.
Количество рядов обрешетки
Суммарное число рядов обрешётки для всей крыши. Чтобы определить количество рядов обрешетки для одного ската, достаточно разделить полученное значение на два.
Равномерное расстояние между досками обрешетки
Чтобы равномерно установить обрешетку, избежав лишнего перерасхода, используйте указанное здесь значение.
Количество досок обрешетки стандартной длиной
Для обрешетки всей крыши вам потребуется указанное здесь количество досок. При расчетах используется стандартная 6-метровая длина доски.
Объем досок обрешетки
Объем досок в метрах кубических поможет вам рассчитать стоимости затрат на обрешетку.
Примерный вес досок обрешетки
Предположительный общий вес досок обрешетки. В расчетах используется средние значения плотности и влажности для хвойных пород дерева.
Угол наклона рельефа на местности: как измерить
Те пользователи, которые работают с рельефом в программе Наш Сад и используют для этого редактор Рельефа, знают: чтобы наклонить поверхность нужно задать угол ее наклона в градусах. Как же определить угол наклона рельефа подручными средствами, если в «кустах», случайно нет теодолита?
Метод вешек
Нам понадобятся: 3 колышка, шнур, рейка жесткая, уровень.
Вбиваем две вешки (колышка) по краям на перепаде высот (см. схему). Забиваем гвоздь или вкручиваем шуруп в произвольной точке С одной из вешек. Замеряем расстояние d от поверхности земли. Привязываем в этом месте шнур и с натяжением закрепляем его к другой вешке в точке А на том же, одинаковом расстоянии d от земли. Берем жесткую рейку, такую, чтобы не прогибалась и закрепляем на ней уровень. Устанавливаем рейку так, чтобы один ее конец находился в точке С, а другой лежал на еще одной вешке. Эту вешку забиваем в землю таким образом, чтобы она касалась натянутого шнура. Рейка на ней должна лежать горизонтально по уровню. Измеряем расстояние DE от шнура до рейки по вертикали и расстояние DС по горизонтали. Согласно схеме это длина рейки. Нам нужно найти значение угла β в градусах. Это и будет искомый угол наклона.
Мы легко можем измерить и вычислить соотношение DE/DC. В тригонометрии это тангенс угла – число, которое определяется соотношением противолежащего и прилежащего к этому углу катетов треугольника CDE. Зная это соотношение можно вычислить величину угла, например, воспользовавшись тригонометрической функцией, обратной тангенсу – арктангенсом.
Вычисляем угол наклона на калькуляторе Windows
Значение арктангенса вычисляем, используя стандартный калькулятор из состава Windows. Щелкаем кнопку «Пуск», переходим в раздел «Все программы», находим «Стандартные» и жмем «Калькулятор». Этот же результат достигнем, нажав сочетание клавиш WIN + R, набрав в строке «Выполнить» команду calc и щелкнув кнопку «OK».
Переключаем калькулятор в режим вычисления тригонометрических функций. Для этого открываем меню «Вид» и находим пункт «Инженерный» или «Научный» (в зависимости от версии используемой операционной системы).
Вводим известное значение тангенса. Это делаем с клавиатуры или щелкая нужные кнопки интерфейса калькулятора.
При этом выбираем единицу измерения «Градусы» – DEG, чтобы получить результат вычисления именно в градусах, а не в радианах или градах. Ставим метку в checkbox (пустом квадратике) с надписью Inv. Так инвертируем значения вычисляемых функций, обозначенные на кнопках калькулятора. Если такого “квадратика” нет, зажимаем кнопку Shift или “↑”. На рисунке слева нужные нам параметры подчеркнуты красной линией.
Щелкаем кнопку с надписью tg или tan (тангенс) и далее « = ». Калькулятор вычисляет значение функции обратной тангенсу – арктангенс. Это значение и будет искомым углом.
Вместо Win-калькулятора можно использовать, например, онлайн-калькуляторы тригонометрических функций. Найти такие сервисы в интернете достаточно легко, задав поиск в браузере.
Важно помнить!
Измерения на местности проводим как можно точнее и рейку устанавливаем точно по уровню. Имейте в виду, что если длина рейки пусть даже полтора-два метра, а длина отрезка АВ метров 15-20, то даже незначительное отклонение уровня от горизонтали дает существенную погрешность. Тем не менее это разумный способ. Он позволяет, пусть и не совсем точно, определить угол наклона рельефа местности.
Используя подобие треугольников АВС и СDЕ можно вычислить также перепад высот: h=АВ*DE/ DС.
как узнать угол наклона ската в градусах, как рассчитать угол стропил двухскатной крыши, узнать и высчитать
Содержание:
Чтобы крыша здания могла в полной мере выполнять все возложенные на нее функции, необходимо при ее создании учесть ряд параметров. Одним из самых важных параметров крыши является ее уклон, который обеспечивает отвод атмосферных осадков с ее поверхности и влияет на способность выдерживать внешние нагрузки. О том, как посчитать наклон крыши, и пойдет речь в данной статье.
Определение наклона крыши — от чего зависит
Чтобы провести правильный расчет уклона крыши, необходимо учитывать несколько факторов, среди которых сильнее всего выделяются следующие:
- Ветровые нагрузки. На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать.
- Снеговые и дождевые нагрузки. Со снегом все довольно просто – повышение угла наклона упрощает его схождение с поверхности кровли. При наклоне крыши более 45 градусов снег почти не будет задерживаться на ней. При малом угле наклона кровли может появляться снеговой мешок, который увеличивает нагрузку на крышу. С дождевыми осадками такая же ситуация – если угол наклона кровли будет слишком низким, то вода сможет затекать в стыки или вообще застаиваться на поверхности крыши.
Отталкиваясь от этих факторов, можно рассчитывать угол наклона скатов. Кроме того, перед тем, как рассчитать угол двухскатной крыши, стоит обратить внимание на рекомендуемые показатели: для местности с сильными ветрами подойдет уклон в 15-20 градусов, а в остальных случаях оптимальная величина уклона составляет 35-40 градусов. Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.
Методика проведения расчетов
При проектировании крыши нужно в обязательном порядке проводить ряд расчетов, среди которых всегда должен присутствовать расчет угла наклона скатов. Данный параметр напрямую влияет на конструкцию крыши: при увеличении наклона снижается снеговая нагрузка, но увеличивается воздействие ветра, поэтому стропильную систему приходится дополнительно усиливать. Для обустройства скатов под большим углом требуется еще и большее количество материалов, что негативно сказывается на стоимости строительства.
Перед тем, как узнать градус наклона крыши, нужно рассчитать эксплуатационную нагрузку на крышу, для чего требуется два параметра:
- Общую массу кровельной конструкции;
- Пиковые уровни снежных осадков, свойственные региону, где проходит строительство.
Упрощенный алгоритм расчетов сводится к следующим действиям:
- Сначала нужно определить вес одного квадратного метра кровельного пирога;
- Полученное значение умножается на общую площадь кровли;
- Масса кровли умножается на коэффициент 1,1.
Пример расчета уклона кровли в градусах
Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.
Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.
Как узнать угол наклона крыши
Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.
Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.
Высота крыши в коньке определяется следующим образом:
- Первым делом нужно рассчитать ширину пролета;
- Полученная величина делится на 2;
- Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.
На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.
Выбор кровельного покрытия в зависимости от наклона крыши
На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.
Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:
- Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
- При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
- Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
- Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.
Заключение
Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода.
Как найти тангенс угла наклона
Под угла наклона обычно понимают угловой коэффициент касательной прямой какой-либо функции. Однако вам может понадобиться также умение найти тангенс угла наклона обычной прямой, например, одной из сторон треугольника по отношению к другой. Определив, что вам надо найти, действуйте одним из следующих способов.
Если вам нужно посчитать угол наклона прямой к оси абсцисс, а вы не знаете уравнение прямой, опустите из любой точки этой прямой (кроме точки пересечения с осью) перпендикуляр на ось. Затем измерьте катеты полученного прямоугольного треугольника и найдите отношение прилежащего катета к противолежащему. Полученное число будет равно тангенсу угла наклона. Этот способ удобно использовать не только для изучения угла наклона прямой, но и для измерения любых углов, как на чертеже, так и в жизни (например, угол ската кровли).
Если вы знаете уравнение прямой, и вам нужно найти тангенс угла наклона этой прямой к оси абсцисс, выразите у через х. В результате вы получите выражение типа у=kх+b. Обратите внимание на коэффициент k – это и есть тангенс угла наклона между положительным направлением оси ох и лучом прямой, расположенным надо этой осью.2+3х, посчитав ее производную, вы получите выражение у`=2х+3. Чтобы найти угловой коэффициент в точке х=3, подставьте это значение в уравнение. В результате несложных вычислений легко можно получить у=2*3+3=9, это и есть искомый тангенс.
Для того чтобы найти тангенс угла наклона одной из сторон треугольника к другой, поступите следующим образом. Найдите синус (sin) этого угла и разделите его на косинус (cos), в результате вы получите тангенс этого угла.
Угол наклона прямой
— Concept
Угол наклона прямой — это угол, образованный пересечением прямой и оси x. Использование горизонтального «пробега» 1 и m для наклона, угла наклона, theta = tan-1 (m) или m = tan (theta). Следовательно, если угол или наклон известны, другое можно найти с помощью одного из уравнений. Если угол наклона отрицательный, то и наклон линии отрицательный.
Какой угол наклона лески? Итак, у меня есть линия, нарисованная здесь уравнением y = mx + b, оно должно быть вам знакомо. Это угол наклона тета, это угол между линией и горизонтом. Теперь я хочу выяснить, как я могу вычислить эту линию, как она соотносится с уравнением линии, поэтому я нарисовал здесь маленький треугольник, а затем я обозначу стороны, скажем, я обозначу это 1, что будет с этой стороны быть? Теперь я знаю, что наклон, наклон линии равен подъему над пробегом, поэтому наклон будет равен вопросительному знаку над 1, так что это будет наклон.
Теперь, если я посмотрю на этот прямоугольный треугольник, и это прямоугольный треугольник, я могу использовать тригонометрию прямоугольного треугольника, чтобы найти связь между тета и m, верно? m — это длина по вертикали этой стороны, поэтому тангенс теты равен m по касательной к 1, тета равен m, так что это соотношение между углом наклона и наклоном, тангенс угла наклона — это наклон, а угол наклона равен арктангенс угла наклона, поэтому вы можете рассчитать наклон по углу наклона, а угол наклона можно рассчитать по углу наклона.
Теперь давайте посмотрим на другой, на несколько частных случаев. Горизонтальные или вертикальные линии. Теперь горизонтальная линия не обязательно будет пересекать ось x, конечно, для линии до y = 0 это ось x, но мы определяем ее угол наклона равным 0, и, конечно же, тангенс 0 равен 0, поэтому наклон будет тангенсом 0, который равен 0, и это то, что мы, как мы определяем наклон горизонтальной линии, это 0.
А как насчет вертикальной? Что ж, я бы сказал, что угол наклона здесь пи больше 2, поэтому тета равен пи больше 2, каков наклон? Касательная к тэте, прямая касательная к пи более 2, но, конечно, это не определено, и это именно то, что мы хотели бы, чтобы наклон вертикальной линии не был определен, нет наклона, поэтому просто для просмотра, угол наклона линии угол, на который Линия определяет отношение к горизонтали, а наклон — это тангенс теты, угол наклона равен наклону, а угол наклона равен обратному тангенсу наклона.
Наклон лески | Аналитическая геометрия
4.3 Наклон прямой (EMBGD)
На диаграмме показано, что прямая линия составляет угол \ (\ theta \) с положительной осью \ (x \). Это называется углом наклона прямой линии.
Мы замечаем, что если градиент изменяется, то значение \ (\ theta \) также изменяется, поэтому угол наклона линии связан с ее градиентом. Мы знаем, что градиент — это отношение изменения направления \ (y \) к изменению направления \ (x \):
\ [m = \ frac {\ Delta y} {\ Delta x} \]
Из тригонометрии мы знаем, что тангенциальная функция определяется как отношение:
\ [\ tan \ theta = \ frac {\ text {противоположная сторона}} {\ text {смежная сторона}} \]
А из схемы видим, что
\ begin {align *}
\ tan \ theta & = \ dfrac {\ Delta y} {\ Delta x} \\
\ поэтому m & = \ tan \ theta \ qquad \ text {for} \ text {0} \ text {°} \ leq \ theta <\ text {180} \ text {°}
\ end {align *}
Следовательно, градиент прямой линии равен касательной к углу, образованному между прямой и положительным направлением оси \ (x \) -.
Вертикальные линии
- \ (\ theta = \ text {90} \ text {°} \)
- Градиент не определен, поскольку нет изменений в \ (x \) — значениях (\ (\ Delta x = 0 \)).
- Следовательно, \ (\ tan \ theta \) также не определено (график \ (\ tan \ theta \) имеет асимптоту в \ (\ theta = \ text {90} \ text {°} \)).
Горизонтальные линии
- \ (\ theta = \ text {0} \ text {°} \)
- Градиент равен \ (\ text {0} \), поскольку нет изменений в \ (y \) — значениях (\ (\ Delta y = 0 \)).
- Следовательно, \ (\ tan \ theta \) также равно \ (\ text {0} \) (график \ (\ tan \ theta \) проходит через начало координат \ ((\ text {0} \ text { °}; 0)) \).
Линии с отрицательными градиентами
Если прямая линия имеет отрицательный градиент (\ (m <0 \), \ (\ tan \ theta <0 \)), то угол, образованный между линией и положительным направлением оси \ (x \) - тупой.
Из диаграммы CAST в тригонометрии мы знаем, что функция касательной отрицательна во втором и четвертом квадранте.Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \ (\ text {180} \ text {°} \), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол во втором квадранте. {- 1} (- \ text {0,7}) \\
& = — \ текст {35,0} \ текст {°}
\ end {align *}
Этот отрицательный угол лежит в четвертом квадранте.Мы должны добавить \ (\ text {180} \) \ (\ text {°} \), чтобы получить тупой угол во втором квадранте:
\ begin {align *}
\ theta & = — \ text {35,0} \ text {°} + \ text {180} \ text {°} \\
& = \ текст {145} \ текст {°}
\ end {align *}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \ (\ theta = \ text {145} \ text {°} \) дает градиент \ (m = — \ text {0,7} \).
Вы справитесь! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки
Угол наклона
Упражнение 4.5
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {60} \ text {°} \\
\ поэтому m & = \ text {1,7}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {135} \ text {°} \\
\ поэтому m & = — \ text {1}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {0} \ text {°} \\
\ поэтому m & = \ text {0}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {54} \ text {°} \\
\ поэтому m & = \ text {1,4}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {90} \ text {°} \\
\ поэтому m & \ text {не определено}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {45} \ text {°} \\
\ поэтому m & = \ text {1}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {140} \ text {°} \\
\ поэтому m & = — \ text {0,8}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {180} \ text {°} \\
\ поэтому m & = \ text {0}
\ end {выровнять *}
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {75} \ text {°} \\
\ поэтому m & = \ text {3,7}
\ end {выровнять *}
строка с \ (m = \ dfrac {3} {4} \)
\ begin {align *}
\ тан \ тета & = м \\
& = \ frac {3} {4} \\
\ theta & = \ tan ^ {- 1} \ left (\ text {0,75} \ right) \\
\ поэтому \ theta & = \ text {36,8} \ text {°}
\ end {выровнять *}
\ begin {align *}
2у — х & = 6 \\
2у & = х + 6 \\
y & = \ frac {1} {2} x + 3 \\
\ тан \ тета & = м \\
& = \ frac {1} {2} \\
\ theta & = \ tan ^ {- 1} \ left (\ text {0,5} \ right) \\
\ поэтому \ theta & = \ text {26,6} \ text {°}
\ end {выровнять *}
прямая проходит через точки \ ((- 4; -1) \) и \ ((2; 5) \)
\ begin {align *}
m & = \ frac {y_2 — y_1} {x_2 — x_1} \\
& = \ frac {5 + 1} {2 + 4} \\
& = \ frac {6} {6} \\
\ поэтому m & = 1 \\
\ тан \ тета & = 1 \\
\ theta & = \ tan ^ {- 1} \ left (\ text {1} \ right) \\
\ поэтому \ theta & = \ text {45} \ text {°}
\ end {выровнять *}
\ begin {align *}
x & = 3y + \ frac {1} {2} \\
x — \ frac {1} {2} & = 3y \\
\ frac {1} {3} x — \ frac {1} {6} & = y \\
\ поэтому m & = \ frac {1} {3} \\
\ theta & = \ tan ^ {- 1} \ left (\ frac {1} {3} \ right) \\
\ поэтому \ theta & = \ text {18,4} \ text {°}
\ end {выровнять *}
линия проходит через точки \ ((2; 5) \) и \ ((\ frac {2} {3}; 1) \)
\ begin {align *}
m & = \ frac {y_2 — y_1} {x_2 — x_1} \\
& = \ frac {1–5} {\ frac {2} {3} -2} \\
& = \ frac {-4} {- \ frac {4} {3}} \\
\ поэтому m & = 3 \\
\ theta & = \ tan ^ {- 1} \ left (\ text {3} \ right) \\
\ поэтому \ theta & = \ text {71,6} \ text {°}
\ end {выровнять *}
линия с градиентом, равным \ (\ text {0,577} \)
\ begin {align *}
m & = \ text {0,577} \\
\ theta & = \ tan ^ {- 1} \ left (\ text {0,577} \ right) \\
\ поэтому \ theta & = \ text {30} \ text {°}
\ end {выровнять *}
Рабочий пример 8: Наклон прямой
Определите угол наклона (с точностью до десятичного знака \ (\ text {1} \)) прямой, проходящей через точки \ ((2; 1) \) и \ ((- 3; -9) \) . {- 1} 2 \\
& = \ текст {63,4} \ текст {°}
\ end {align *}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусов).
Напишите окончательный ответ
Угол наклона прямой равен \ (\ text {63,4} \) \ (\ text {°} \).
Рабочий пример 9: Наклон прямой
Определите уравнение прямой, проходящей через точку \ ((3; 1) \) с углом наклона \ (\ text {135} \ text {°} \).
Используйте угол наклона для определения уклона линии
\ begin {align *}
м & = \ загар \ тета \\
& = \ tan \ text {135} \ text {°} \\
\ поэтому m & = -1
\ end {align *}
Запишите градиентно-точечную форму уравнения прямой линии
\ [y — y_1 = m (x — x_1) \]
Заменитель \ (m = -1 \)
\ [y — y_1 = — (x — x_1) \]
Заменить данную точку \ ((3; 1) \)
\ begin {align *}
у — 1 & = — (х — 3) \\
у & = -x + 3 +1 \\
& = -x + 4
\ end {align *}
Напишите окончательный ответ
Уравнение прямой: \ (y = -x + 4 \).
Рабочий пример 10: Наклон прямой
Определите острый угол (с точностью до десятичного знака \ (\ text {1} \)) между линией, проходящей через точки \ (M (-1; 1 \ frac {3} {4}) \) и \ (N (4; 3) \) и прямая \ (y = — \ frac {3} {2} x + 4 \).
Нарисуйте эскиз
Проведите линию через точки \ (M (-1; 1 \ frac {3} {4}) \) и \ (N (4; 3) \) и линию \ (y = — \ frac {3} { 2} x + 4 \) на подходящей системе осей. Метки \ (\ alpha \) и \ (\ beta \), углы наклона двух линий.Обозначьте \ (\ theta \), острый угол между двумя прямыми линиями.
Обратите внимание, что \ (\ alpha \) и \ (\ theta \) — острые углы, а \ (\ beta \) — тупой угол.
\ [\ begin {array} {rll}
\ hat {B} _1 & = \ text {180} \ text {°} — \ beta & (\ angle \ text {on str. line}) \\
\ text {and} \ theta & = \ alpha + \ hat {B} _1 \ quad & (\ text {ext.} \ angle \ text {of} \ треугольник = \ text {sum int. opp}) \\
\ поэтому \ theta & = \ alpha + (\ text {180} \ text {°} — \ beta) \\
& = \ text {180} \ text {°} + \ alpha — \ beta
\ конец {массив} \]
Используйте градиент, чтобы определить угол наклона \ (\ beta \)
Из уравнения \ (y = — \ frac {3} {2} x + 4 \) мы видим, что \ (m <0 \), поэтому \ (\ beta \) - тупой угол такой, что \ (\ text {90} \ text {°} <\ beta <\ text {180} \ text {°} \). {- 1} \ left (\ frac {1} {4} \ right) \\ & = \ текст {14,0} \ текст {°} \ end {align *}
Напишите окончательный ответ
\ begin {align *}
\ theta & = \ text {180} \ text {°} + \ alpha — \ beta \\
& = \ text {180} \ text {°} + \ text {14,0} \ text {°} — \ text {123,7} \ text {°} \\
& = \ текст {70,3} \ текст {°}
\ end {align *}
Острый угол между двумя прямыми равен \ (\ text {70,3} \) \ (\ text {°} \).{-1} \ left (- \ frac {9} {2} \ right) \\
& = — \ text {77,5} \ text {°} \\
\ поэтому \ theta & = \ text {180} \ text {°} — \ text {77,5} \ text {°} \\
\ поэтому \ theta & = \ text {102,5} \ text {°}
\ end {выровнять *}
линия, проходящая через \ ((- 1; -6) \) и \ ((- \ frac {1} {2}; — \ frac {11} {2}) \)
\ begin {align *}
m & = \ frac {y_2 -y_1} {x_2 — x_1} \\
& = \ frac {- \ frac {11} {2} + 6} {- \ frac {1} {2} +1} \\
& = \ frac {\ frac {1} {2}} {\ frac {1} {2}} \\
\ поэтому m & = 1 \\
\ theta & = \ tan ^ {- 1} \ left (1 \ right) \\
\ поэтому \ theta & = \ text {45} \ text {°}
\ end {выровнять *}
\ begin {align *}
5 & = 10л — 15х \\
5 + 15x & = 10л \\
\ frac {1} {2} + \ frac {3} {2} x & = y \\
\ поэтому m & = \ frac {3} {2} \\
\ theta & = \ tan ^ {- 1} \ left (\ frac {3} {2} \ right) \\
\ поэтому \ theta & = \ text {56,3} \ text {°}
\ end {выровнять *}
\ begin {align *}
m & = \ frac {y_2 -y_1} {x_2 — x_1} \\
& = \ frac {3 + 1} {2–0} \\
& = \ frac {4} {2} \\
\ поэтому m & = 2 \\
\ theta & = \ tan ^ {- 1} \ left (2 \ right) \\
\ поэтому \ theta & = \ text {63,4} \ text {°}
\ end {выровнять *}
\ begin {align *}
m & = \ frac {y_2 -y_1} {x_2 — x_1} \\
& = \ frac {2 — 0} {0 — 6} \\
& = \ frac {2} {- 6} \\
\ поэтому m & = — \ frac {1} {3} \\
\ theta & = \ tan ^ {- 1} \ left (- \ frac {1} {3} \ right) \\
\ поэтому \ theta & = — \ text {18,4} \ text {°} \\
\ поэтому \ theta & = \ text {180} \ text {°} — \ text {18,4} \ text {°} \\
\ поэтому \ theta & = \ text {161,6} \ text {°}
\ end {выровнять *}
Градиент undefined
Определите острый угол между прямой, проходящей через точки \ (A (-2; \ frac {1} {5}) \) и \ (B (0; 1) \), и прямой, проходящей через точки \ ( C (1; 0) \) и \ (D (-2; 6) \).{-1} \ влево (-2 \ вправо) \\
\ поэтому \ alpha & = — \ text {63,4} \ text {°} \\
\ поэтому \ alpha & = \ text {180} \ text {°} — \ text {63,4} \ text {°} \\
\ поэтому \ alpha & = \ text {116,6} \ text {°} \\
\ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ angle \ треугольник) \\
\ поэтому \ theta & = \ text {21,8} \ text {°} + (\ text {180} \ text {°} — \ text {116,6} \ text {°}) \\
& = \ текст {85,2} \ текст {°}
\ end {выровнять *}
Определите угол между линией \ (y + x = 3 \) и линией \ (x = y + \ frac {1} {2} \).{-1} \ left (1 \ right) \\
\ поэтому \ beta & = \ text {45} \ text {°} \\
\ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ angle \ треугольник) \\
\ поэтому \ theta & = \ text {45} \ text {°} + (\ text {180} \ text {°} — \ text {135} \ text {°}) \\
& = \ текст {90} \ текст {°}
\ end {выровнять *}
Найдите угол между прямой \ (y = 2x \) и прямой, проходящей через точки \ ((- 1; \ frac {7} {3}) \) и \ ((0; 2) \).
Пусть угол наклона линии \ (y = 2x \) равен \ (\ beta \), а угол наклона другой линии равен \ (\ alpha \).{-1} \ left (2 \ right) \\
\ поэтому \ beta & = \ text {63,4} \ text {°} \\
m & = \ frac {y_2 -y_1} {x_2 — x_1} \\
& = \ frac {2 — \ frac {7} {3}} {0 + 1} \\
& = \ frac {- \ frac {1} {3}} {1} \\
\ поэтому m & = — \ frac {1} {3} \\
\ поэтому \ alpha & = — \ text {18,4} \ text {°} \\
\ поэтому \ alpha & = \ text {180} \ text {°} — \ text {18,4} \ text {°} \\
\ поэтому \ alpha & = \ text {161,6} \ text {°} \\
\ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ угол \ треугольник) \\
\ поэтому \ theta & = \ text {63,4} \ text {°} + (\ text {180} \ text {°} — \ text {161,6} \ text {°}) \\
& = \ текст {81,8} \ текст {°}
\ end {выровнять *}
Градиент (или наклон) линии и наклон
Приложение: Дорожный знак, обозначающий крутой уклон.
Уклон дороги «15%» эквивалентен «m = 0,15».
Уклон (также известный как уклон ) линии определяется как
`» gradient «= текст (вертикальный подъем) / текст (горизонтальный бег`
На следующей диаграмме градиент линии AB определяется как: `a / b`
Как правило, для линии, соединяющей точки ( x 1 , y 1 ) и ( x 2 ,
у 2 ) имеем:
Теперь мы можем написать формулу для наклона прямой.
Градиент линии формулы
Как видно из диаграммы выше, угол наклона (обычно обозначается как м ) определяется как:
`m = (y_2-y_1) / (x_2-x_1`
Интерактивный график — наклон прямой
Вы можете изучить концепцию наклона линии на следующем интерактивном графике (это не фиксированное изображение).
Перетащите либо точку A ( x 1 , y 1 ) или точку B ( x 2 , y 2 градиент), чтобы исследовать, как градиент работает.Числа будут обновляться по мере взаимодействия с графиком.
Обратите внимание, что происходит со знаком (плюс или минус) наклона, когда точка B находится выше или ниже A.
Наклон `= (y_2 — y_1) / (x_2 — x_1)`
`= (BC) / (AC)`
Авторские права © www.intmath.com
Вы можете перемещать график вверх-вниз, влево-вправо, если удерживаете клавишу «Shift», а затем перетаскиваете график.
Если заблудились, всегда можно обновить страницу.
Пример
Найдите наклон прямой, соединяющей точки (−4, −1) и (2, −5).
Ответ
Это задействованные точки:
Итак, уклон:
`m = (y_2-y_1) / (x_2-x_1`
`= (- 5 — (- 1)) / (2 — (- 4)`
`= (- 4) / 6`
`= -2 / 3`
Обратите внимание, что наклон отрицательный . Линия идет «вниз по склону», когда мы движемся слева направо.
Положительные и отрицательные склоны
Как правило, положительный наклон указывает на значение зависимой переменной (обычно y ) увеличивается на при движении слева направо:
Зависимая переменная на приведенном выше графике — это значение y , а независимая переменная — x .
Отрицательный наклон означает, что значение зависимой переменной (обычно y ) равно , уменьшаясь на при движении слева направо:
Наклон
У нас есть линия с уклоном м и углом, который линия составляет с
x — ось α.
Из тригонометрии напомним, что тангенс угла α определяется как:
`tan \ alpha = текст (напротив) / текст (рядом)`
Теперь, поскольку наклон также определяется как противоположный / смежный, мы имеем:
Это дает нам результат:
tan α = м
Тогда мы можем найти угол α , используя
α = arctan м
(то есть α = tan -1 м )
Этот угол α называется наклоном линии.@ `
ПРИМЕЧАНИЕ: Размер угла α составляет (по определению) только
между `0 °` и `180 °`.
Упражнение 2
Найдите наклон прямой α = 137 °.
Ответ
Ситуация следующая:
Итак, уклон:
м = tan α
= загар 137 °
= -0,933
Обратите внимание, что наклон отрицательный.
Уголки Углы подъема или наклона
Две десятых мили составляют 0,2 × 5280 футов = 1056 футов, так что это мое горизонтальное расстояние. Мне нужно найти высоту х кактуса.Я рисую прямоугольный треугольник и маркирую все, что знаю: .
До ближайшей ноги г.
Мне нужно выполнить это упражнение Чтобы минимизировать ошибку округления, я буду использовать Теперь, когда у меня есть длина основания, Отлично! Сохраняя все цифры Вверх | Вернуться к индексу
| НАЙТИ УРОК Этот урок можно распечатать для личного пользования. | |
Угол наклона склона
Проще говоря, угол наклона — это мера расстояния между двумя линиями на графике. Поскольку линии на графике часто рисуются по диагонали, это пространство обычно имеет треугольную форму. Поскольку все треугольники измеряются их углами, это пространство между двумя линиями часто должно быть представлено «углами» наклона. Когда наклон линии не может быть измерен обычным способом, мы можем использовать угол наклона, потому что угол наклона и наклон линии фактически равны.
Наклон
Наклон — это отношение отклонения от вертикали к горизонтали линии на графике. Обычно это обозначается буквой m. Чем больше наклон линии, тем она круче. Если наклон представлен отрицательным числом, тогда линия на графике движется не вверх, а вниз.
Наклонение
На обычном графике оси x и y делят пополам друг друга на перпендикуляре и образуют четыре прямых угла.На графике, где единственными линиями являются x и y, наклон всегда будет составлять 90 градусов. Это связано с тем, что наклон является мерой положительного участка оси x (два верхних квадранта графика) до тех пор, пока он не достигнет линии. В этом случае, поскольку единственная другая линия является осью Y, наклон охватывает весь верхний правый квадрант графика, составляя наклон 90 градусов. Любая горизонтальная линия имеет наклон 0, а любая вертикальная линия имеет наклон 90. Следует отметить, что горизонтальные линии отражают ось x, а вертикальные линии — ось y.
Функция тангенса
Функция тангенса используется в тригонометрии для определения меры угла в треугольнике. Касательная измеряет только угол между двумя линиями треугольника, которые не являются гипотенузой. Эту функцию не следует путать с другой касательной в математике, которая также имеет отношение к наклонам. Эта касательная — это точка, в которой наклон касается кривой другой функции. Что касается угла наклона склона, тангенс используется только для измерения угла и не используется никаким другим способом.
Угол наклона
Угол наклона откоса — это мера наклона от оси x к линии или наклона на графике. Как и в случае с мерой наклона на графике, это мера угла, образованного между положительным участком оси x, движущимся против часовой стрелки, пока не достигнет наклона линии. Если наклон линии положительный, она проходит через правый верхний квадрант графика, и угол будет небольшим. Если наклон линии отрицательный, она проходит через верхний левый квадрант, и угол будет большим.Функция касательной используется для измерения этого угла и рассматривает ось x как одну линию треугольника, а наклон этой линии — как другую касательную линию. Наклон прямой и касательная всегда будут равны друг другу.
Расчет уклона, уклона, наклона или уклона
Карта сайта> Строительство> Расчет уклона
Расчет уклона по длине и высоте
Расчет уклона с использованием ширины и высоты для определения процента, угла или длины уклона (гипотенуза *) часто используется во многих областях, особенно в строительной отрасли, такой как лестницы или крыши.
Определение уклона
Наклон соответствует наклону поверхности или линии по отношению к горизонтали. Его можно измерить как угол в градусах, радианах или градусах или в процентах (отношение ширины к высоте, умноженное на 100).
Вы можете получить все необходимые значения для наклона крыши, уклона дренажа, крутого пути, аппарели и т. Д.
Расчет уклона
Наклон, гипотенуза и углы прямоугольного треугольника
Квартир:
дюймфутюрдмайлммсмдммдмхмкм
знаков после запятой:
012345678910
| Наклон: | 75,00% |
Длина откоса: | 5,00 м |
Угол 1: | 36,87 ° |
Угол 2: | 53,13 ° |
Периметр треугольника: | 12,00 м |
Поверхность треугольника: | 6,00 м 2 |
* Гипотенуза: Абсолютно варварский термин, означающий «длину третьей стороны» или «длину склона».
Формула для расчета уклона
Длина откоса рассчитывается по теореме Пифагора. Эта теорема получается путем умножения квадратного корня на сумму квадрата ширины и возведенной в квадрат высоты.
Итак: Квадратный корень ((ширина x ширина) + (высота x высота)) = длина уклона
Наклон 100%
Следует отметить, что уклон в 100% не является вертикальным, но он эквивалентен одинаковой высоте и ширине, что приводит к углу наклона 45 °.Например: горная тропа со 100% уклоном будет подниматься на 100 метров на каждые 100 метров, когда она идет вперед. Расстояние по этому склону составит 141,4 метра.
Пандусы для инвалидов
Уклоны пандуса для инвалидов должны быть:
- максимум 12% при длине менее 50 см
- максимум 8% для длины менее 8 м
- от 4% до 5% для максимальной длины 10 м
Лестницы должны устанавливаться каждые 10 м и иметь минимальную длину 1.40 мес.
Наклон ширины, известный как поперечный уклон, предпочтительно должен быть нулевым и во всех случаях менее 2%. Ширина пандуса должна быть не менее 1,40 м. Его можно уменьшить до 1,20 м, если нет стены с одной или другой стороны.
Наклон ширины, также известный как поперечный наклон, предпочтительно должен быть нулевым и никогда не должен превышать 2%. Ширина пандуса должна быть не менее 1,40 м. Его можно уменьшить до 1,20 м, если одна сторона не прикреплена к стене.
Средний наклон и высота трассы
Вполне возможно рассчитать средний угол наклона пути, используя значения, заданные горизонтальным расстоянием (пробег) и высотой (подъемом), достигнутыми в конце уклона.Если путь ветреный, пройденное расстояние будет больше, чем длина склона.
Рисование под прямым углом
Длина ската соответствует диагонали прямоугольного треугольника. Вы также можете использовать это измерение для вычисления диагонали, чтобы нарисовать прямой угол, метод, широко используемый в строительной отрасли. Обычно используются следующие значения: 3 метра, 4 метра и 5 метров до , чтобы получить прямой угол . К сожалению, использовать такие измерения не всегда возможно.Подставив значения 3 метра и 4 метра на значения, полученные на месте, и результат длины склона (используемый в качестве диагонали), позволит вам правильно нарисовать прямой угол.
Калькулятор уклона
По определению, уклон или уклон линии описывает ее крутизну, уклон или уклон. Где м — уклон |
Если известны 2 точки
Если известны 1 точка и наклон
Уклон, иногда называемый в математике градиентом, — это число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается м .Как правило, крутизна линии измеряется абсолютным значением ее уклона, м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , на основе ее знака и значения:
- Линия увеличивается и идет вверх слева направо, когда m> 0
- Линия убывает и идет вниз слева направо, когда m <0
- Линия имеет постоянный наклон и является горизонтальной при m = 0
- Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в знаменателе.См. Приведенное ниже уравнение.
Наклон — это, по сути, изменение высоты при изменении горизонтального расстояния, и его часто называют «подъем за счет пробега». Он находит применение в градиентах в географии, а также в гражданском строительстве, например, в строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница расстояний между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы учитывать кривизну земли. как фактор.Математически наклон представлен как:
В приведенном выше уравнении y 2 — y 1 = Δy или вертикальное изменение, а x 2 — x 1 = Δx или горизонтальное изменение, как показано на представленном графике. Также можно увидеть, что Δx и Δy — это отрезки прямых, которые образуют прямоугольный треугольник с гипотенузой d , причем d — это расстояние между точками (x 1 , y 1 ) и (x 2 , y 2 ) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , указанный в калькуляторе выше. Кратко:
d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2
Приведенное выше уравнение является теоремой Пифагора в своем корне, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками. .Учитывая две точки, можно найти θ , используя следующее уравнение:
м = тангенс угла (θ)
По точкам (3,4) и (6,8) найдите наклон линии, расстояние между двумя точками и угол наклона:
d = √ (6-3) 2 + (8-4) 2 = 5
Хотя это выходит за рамки данного калькулятора, помимо его основного линейного использования, концепция наклона важна в дифференциальном исчислении.
 Так, чем больший угол, тем больше потребуется материала для покрытия плоскостей.
Так, чем больший угол, тем больше потребуется материала для покрытия плоскостей.