Как уклон считается: Как посчитать уклон в процентах. Угол уклона кровли для различных условий и кровельных материалов

Уклон и Конусность — Определение, обозначение на чертеже, формула расчёта уклона и конусности ChertimVam.Ru

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.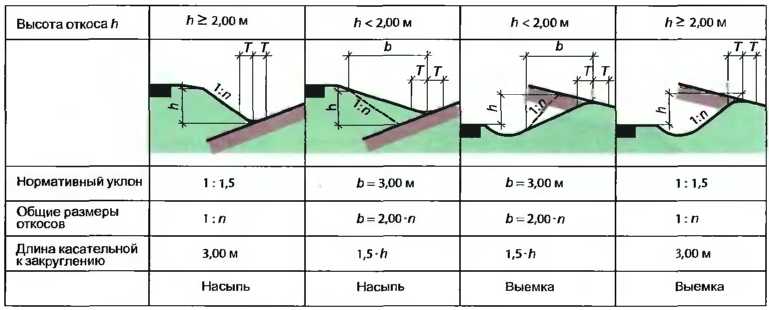
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Уклон плоских крыш — База знаний ТЕХНОНИКОЛЬ

Уклон крыши необходим для эффективного отвода воды с поверхности ската.

При нарушении уклона крыши образуются застойные зоны, которые способствуют сокращению срока службы водоизоляционного ковра.

Крыша с большим уклоном «прощает» мелкие ошибки при монтаже и увеличивает срок службы конструкции.

В чем измеряется уклон крыши

Уклоном называют величину крутизны ската крыши.

Если представить крышу в разрезе, то получится прямоугольный треугольник. Уклоном будет считаться тангенс угла α, который равен отношению противолежащего катета к прилежащему.

Уклон может измеряться в градусах – °, процентах – %, а также может быть выражен коэффициентом уклона i.

Крыши с уклоном до 12° принято считать плоскими, а с уклоном 12° и более — скатными.

Перевод уклона из градусов в проценты

Для перевода уклона из градусов в проценты следует тангенс угла в градусах умножить на 100:

Для перевода уклона из процентов в градусы следует вычислить функцию арктангенса угла в процентах, умноженного на 0,01:

Сводная таблица с уклонами в различных величинах

Минимальный уклон крыши

В соответствии с действующими нормативными документами в строительстве, устройство скатов крыши необходимо выполнять с уклоном не менее 1,5% (i=0,015, 0,9°), т. е. 1,5 см подъема ската крыши на 100 см длины.

9. Уклон

Уклон – это мера изменения высоты. Это важный параметр в нескольких известных прогностических моделях, используемых для управления окружающей средой, включая универсальное уравнение потери почвы и сельскохозяйственные модели загрязнения из неточечных источников.

Один из способов выразить наклон в процентах. Чтобы вычислить уклон в процентах, разделите разницу между высотами двух точек на расстояние между ними, а затем умножьте частное на 100. Разница в высотах между точками называется подъемом. Расстояние между точками называется пробегом. Таким образом, процент уклона равен (подъем/спуск) x 100.

Рисунок 7.10.1 Расчет наклона в процентах. Подъем на 100 футов над пробегом в 100 футов дает 100-процентный уклон. Подъем на 50 футов над 100-футовым пробегом дает 50-процентный уклон.

Еще один способ выразить наклон – это угол наклона или градус наклона. Как показано ниже, если вы визуализируете подъем и бег как стороны прямоугольного треугольника, то градус наклона — это угол, противоположный подъему. Поскольку степень наклона равна тангенсу дроби подъем/набег, ее можно рассчитать как арктангенс подъема/набега.

Рисунок 7.10.2 Подъем на 100 футов на участке длиной 100 футов дает угол наклона 45°. Подъем на 50 футов на протяжении 100 футов дает угол наклона 26,6°.

Вы можете рассчитать уклон на контурной карте, анализируя расстояние между горизонталями. Однако, если вам нужно рассчитать много значений уклона, вы захотите автоматизировать процесс. Оказывается, расчеты уклона гораздо проще выполнять для данных высот с координатной сеткой, чем для векторных данных, поскольку высоты более или менее равномерно распределены в растровых сетках.

Было разработано несколько алгоритмов для расчета процента наклона и степени наклона. Самый простой и распространенный метод называется методом соседства . Метод соседства вычисляет уклон в одной точке сетки путем сравнения высот восьми точек сетки, которые ее окружают.

Рисунок 7.10.3 Алгоритм соседства оценивает процентный уклон в ячейке 5 путем сравнения высот соседних ячеек сетки.

Алгоритм соседства оценивает процентный уклон в ячейке сетки 5 (Z ₅ ) в виде суммы абсолютных значений уклона восток-запад и уклона север-юг и умножения суммы на 100. На рис. 7.10.4 показано, как рассчитываются уклон восток-запад и уклон север-юг. По существу, уклон с востока на запад оценивается как разница между суммами высот в первом и третьем столбцах матрицы 3 x 3. Точно так же наклон с севера на юг представляет собой разницу между суммами высот в первой и третьей строках (обратите внимание, что в каждом случае среднее значение взвешивается в два раза).

Рисунок 7.10.4 Алгоритм соседства для расчета процентного уклона.

Щелкните здесь, чтобы просмотреть текстовую версию уравнения, показанного на изображении выше.

На иллюстрации показано, как уклон местности в заданной ячейке сетки высот можно рассчитать на основе высот восьми окружающих ее ячеек сетки. Во-первых, наклон север-юг рассчитывается из столбцов сетки. Затем по рядам сетки рассчитывается уклон с востока на запад. Квадратный корень из суммы наклона с севера на юг и уклона с востока на запад, умноженный на 100, равен наклону в процентах в исходной ячейке сетки. Причудливый технический термин для этой процедуры — «алгоритм соседства».

Алгоритм окрестности вычисляет уклон для каждой ячейки в сетке высот путем анализа каждой окрестности 3 x 3. Процентный уклон можно преобразовать в градусы позже. Результатом является сетка значений уклона, подходящая для использования в различных моделях потери почвы и гидрологических моделях.

Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона
(Бесплатный онлайн-инструмент вычисляет уклон по 2 точкам)

Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.

Разные слова, та же формула

Учителя используют разные слова для координат y и координат x.

1. Некоторые называют координаты у подъемом, а координатами х — бег.
2. Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .

Все эти слова означают то же самое, что и , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!

Пример 1

Наклон прямой , проходящей через точку (1, 2) и точку (4, 3), равен $$ \frac{1}{3}$$.

Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.

Может ли любая из точек быть $$( x_1 , y_1 ) $$ ?

Есть только один способ узнать!

Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .

Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .

Работа рядом

точка (4, 3) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$

точка (1, 2) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$

Ответ: , а не не имеет значения, какую точку поставить первой. Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом!
$$ \фракция{1}{3} $$

Пример 2 наклона линии А

Наклон прямой , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Видеоруководство по наклону линии

Наклон вертикальных и горизонтальных линий

Наклон вертикальной линии не определен

Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).

Наклон горизонтальной линии равен нулю

Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль. Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».

Любые две точки на прямой имеют одинаковый наклон?

Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.

Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать 90 155 любых 90 156 2 точек на линии.

Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.

Как вы можете видеть ниже, наклон одинаков независимо от того, какие 2 точки вы выбрали.

Наклон линии

Никогда не меняется

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона
(Бесплатный онлайн-инструмент вычисляет уклон по 2 точкам)

Практика Проблемы

Проблема 1

Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$

$
\frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3}
\\
= \ в коробке {-2 }
$

Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$

$ \frac{3- \red 9{10- \красное 7}
\\ =\ гидроразрыв{-6}{3}
\\
= \в коробке{-2}
$

Проблема 2

Прямая проходит через (4, -2) и (4, 3). Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$

$
= \frac{-2 — \red 3}{4- \red 4}
«=»
\frac{-5}{\color{red}{0}}
\\ = \text{неопределенный}
$

Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$

$
= \frac{3- \red{-2}}{4- \red 4}
«=»
\frac{5}{\color{red}{0}} \\
= \текст{неопределенный}
$

Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.

Проблема 3

Прямая проходит через (2, 10) и (8, 7). Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$

$
\frac{10 — \red 7}{2 — \red 8}
\\ = \ гидроразрыва {3}{-6}
\\ = -\фракция{1}{2}
$

Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$

$
\frac{7 — \red {10}}{8- \red 2}
\\ = \ гидроразрыв {-3} {6}
\\ = -\фракция{1}{2}
$

Проблема 4

Прямая проходит через (7, 3) и (8, 5). Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$

$$
\frac{ 5- \red 3}{8- \red 7}
\\
= \ гидроразрыва {2} {1}
\\ = 2
$$

Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$

$$
\frac{ 3- \red 5}{7- \red 8}
\\= \фракция{-2}{-1}
\\ = 2
$$

Проблема 5

Прямая проходит через (12, 11) и (9, 5) .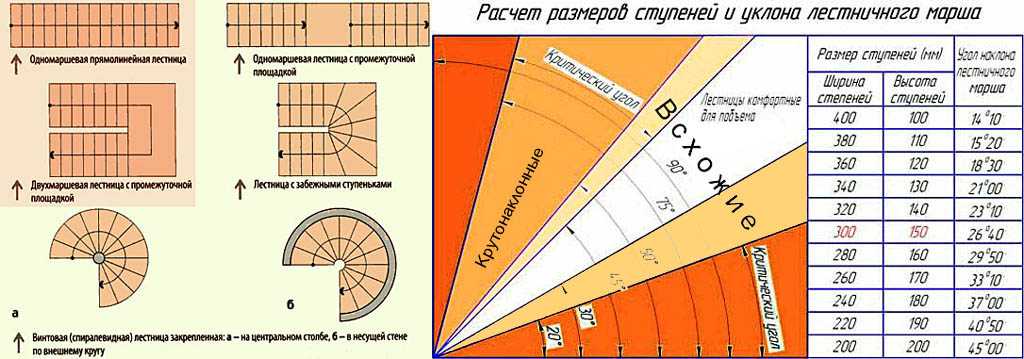 Каков его наклон?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$

$$
\frac{ 11 — \red 5}{12- \red 9}
\\ = \ гидроразрыва {6} {3}
\\ =2
$$

Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$

$$ \frac{ 5- \red{ 11} }{9- \red { 12}}
\\ = \фракция{-6}{-3}
\\ = 2$$

Проблема 6

Каков наклон линии, проходящей через (4, 2) и (4, 5)?

$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

$

Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$

$$
\frac{ 2 — \red 5}{4- \red 4}
\\ = \frac{-3}{\color{red}{0}}
\\ = не определено
$$

Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$

$$
\frac{ 5 — \red 2}{4- \red 4}
\\ = \frac{ 3}{\color{red}{0}}
\\ = не определено
$$

ПРЕДУПРЕЖДЕНИЕ! Уловите ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ . У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?

Задача-вызов

Найдите наклон прямой через две точки.

Попытка №1

$
наклон = \ гидроразрыв {подъем} {бег}
\\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}}
«=»
\ гидроразрыв {6-3} {1-2}
\\= \фракция{3}{-1}
=\в коробке{-3}
$

Попытка №2

$$
наклон = \ гидроразрыв {подъем} {бег}
\\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}}
«=»
\фракция{6-3}{2-1}
\\= \фракция{3}{1}
\\
= \в коробке{3}
$$

Попытка №3

$$
уклон = \ гидроразрыв {подъем} {бег}
\\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}}
\\ =\ гидроразрыва {2-1} {6-3}
\\ =\в коробке{ \frac{1}{3}}
$$

Правильный ответ — попытка №2.

В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:

$$
\frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}}
$$

Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!

$$
\ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}}
$$

Slope Practice Генератор проблем

Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.