Коэффициент теплопередачи, формула и примеры
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Коэффициенты Коэффициент теплопередачи
Определение и формула коэффициента теплопередачи
Процесс теплопередачи можно разделить на теплоотдачу энергии горячим веществом стенке, процесс теплопроводности внутри стенки и теплоотдачу стенки энергии холодному веществу.
Поток тепла при стационарной теплопередаче величина постоянная, то есть не зависит от времени и координат.
Теплопередача через плоскую стенку
Рассмотрим плоскую стенку, через которую происходит теплопередача. Поток тепла через нее равен:
где — температура холодного вещества (), — температура горячего вещества, S — площадь стенки, — коэффициент теплопередачи.
Коэффициентом теплопередачи через плоскую стенку является физическая величина () равная:
где — коэффициент теплоотдачи от первой среды к стенке, — коэффициент теплоотдачи от стенки ко второй среде, — толщина стенки, — коэффициент теплопроводности стенки.
Теплопередача через цилиндрическую стенку
Поток тепла свозь стенку в виде цилиндра вычисляют при помощи формулы:
где — линейный коэффициент теплопередачи, — высота цилиндра.
Линейным коэффициентом теплопередачи через стенку в виде цилиндра является физическая величина () равная:
где — внутренний диаметр цилиндра, — внешний диаметр цилиндра. Для цилиндрических стенок, у которых для расчета теплопередачи применяют формулы (1) и (2) для плоской стенки. Если цилиндр (труба) выполнен из материала с высокой теплопроводностью, то величина термического сопротивления () стенки стремится к нулю ( ), тогда коэффициент теплопроводности рассчитывают по формуле:
Теплопередача через шаровую стенку
Поток тепла через шаровую стенку с внутренним диаметром и наружным — , которая разделяет две среды с постоянными температурами и равен:
Линейным коэффициентом теплопередачи через стенку в виде шара является физическая величина () равная:
Единицы измерения коэффициента теплопередачи
Основной единицей измерения коэффициента теплопередачи в системе СИ является:
=Вт/м2К
=Вт/мК
=Вт/К
Примеры решения задач
|
Понравился сайт? Расскажи друзьям! |
| ||
компании «Промавто» в 2008 году был построен испытательный комплекс и Все «Как, его выбрать». Теоретический коэффициент
холодильная система, установленная на
Для определения разности
Наша новая измерительная лаборатория находится по адресу: Нижний Новгород, Казанское шоссе, дом 12. См. схему проезда в разделе «Контакты»Измерения фургонов выполняет ООО «Тепломер». Подробности — Тел. +7 920 293-33-53 Назад в 2001 год | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
фото), спроектированная и построенная в начале 2008 года.
Только
п. и поэтому иногда называется общим или даже интегральным коэффициентом теплопередачи.
Внутри фургона в момент съемки было около +30°С,
Технические требования и методы
Провода от датчиков температуры имеют длину по 6 метров, так
Две двери покрываются
КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
Коэффициент теплоотдачи – количественная характеристика конвективного теплообмена между текучей средой (жидкостью) и поверхностью (стенкой), обтекаемой жидкостью.
Эта характеристика появляется как коэффициент пропорциональности a в соотношении Ньютона-Рихмана
где – плотность теплового потока на стенке, T w температура стенки, T t характерная температура жидкости, например, температура T e вдали от стенки во внешнем потоке, температура объемного потока Т б в трубах и т. д. Единицей измерения в международной системе единиц (СИ) (см. Международная система единиц) является Вт/(м 2 К), 1 Вт/(м 2 К) = 0,86 ккал/(м 2 ч°C) = 0,1761 БТЕ/(hft 2 °F) или 1 ккал/(м 2 ч° C) = 1,1630 Вт/(м 2 К), 1 БТЕ/(hft 2 °F) = 5,6785 Вт/(м 2 К). Коэффициент теплоотдачи получил широкое распространение в расчетах конвективного теплообмена и при решении задач внешнего теплообмена между теплопроводной твердой средой и окружающей ее средой. Коэффициент теплоотдачи зависит как от тепловых свойств среды, гидродинамических характеристик ее течения, так и от гидродинамических и тепловых граничных условий.
Используя методы теории подобия, зависимость коэффициента теплоотдачи от многих факторов во многих практически важных случаях может быть представлена в виде компактных соотношений между безразмерными параметрами, известных как критерии подобия. Эти соотношения называются обобщенными или уравнениями подобия (формулами). В качестве безразмерного числа для теплообмена в этих уравнениях используется число Нуссельта Nu = αl/λf или число Стэнтона St =, где 1 – характерный размер поверхности в потоке, массовая скорость потока жидкости, λ f и C pf теплопроводность и теплоемкость жидкости. При решении задач теплопроводности в твердом теле часто в качестве граничного условия задается распределение коэффициента теплоотдачи α между телом и окружающей его средой. Здесь полезно использовать безразмерный независимый параметр — число Био Bi = αl/λ s , где λ s — теплопроводность твердого тела, а 1 — его характерный размер. Зависимость чисел Nu и St от чисел Re и Pr играет существенную роль в переносе тепла принудительной конвекцией.
В случае полностью развитого теплообмена в круглой трубе с ламинарным течением жидкости число Нуссельта является константой, а именно Nu = 3,66 при постоянной температуре стенки и 4,36 при постоянном тепловом потоке (см. Трубы (однофазный теплообмен в ) ). В случае свободной конвекции число Nu зависит от чисел Gr и Pr. Когда теплоемкость жидкости существенно различается, коэффициент теплопередачи часто определяют через разность энтальпий (h w – h f ). Понятие коэффициента теплоотдачи используется также при теплообмене с фазовыми превращениями в жидкости (кипение, конденсация). В этом случае температура жидкости характеризуется температурой насыщения T s . Порядок величины коэффициента теплоотдачи для различных случаев теплообмена представлен в таблице 1.
При анализе внутреннего теплообмена в пористых телах, т. е. конвективного теплообмена между жесткой матрицей и проницаемой через нее жидкостью, часто используют объемный коэффициент теплоотдачи
где qv — тепловой поток, переходящий от жесткой матрицы к жидкости в единице объема пористого тела, T w — локальная температура матрицы, T f — локальная объемная температура жидкости.
Следует подчеркнуть, что постоянство α в широком диапазоне и ΔT (при прочих равных условиях) встречается только в случае конвективного теплообмена, когда физические свойства жидкости при теплообмене изменяются незначительно. При конвективном теплообмене в жидкости с переменными свойствами и при кипении коэффициент теплоотдачи может существенно зависеть от и ΔT . В этих случаях увеличение теплового потока может привести к таким опасным явлениям, как выгорание (переходный тепловой поток) и ухудшение турбулентного теплообмена в трубах. Если (ΔT) является нелинейным, представляется нецелесообразным представлять его через коэффициент α при анализе, например, стабильности кипения.
Общий коэффициент теплопередачи
где T f1 и T f2 – температуры нагрева и нагрева жидкости, используется при расчетах теплообмена между двумя жидкостями через разделяющую стенку. Значения U для наиболее часто используемых конфигураций стен определяются по формулам
для плоской многослойной стены,
для цилиндрической многослойной стенки и
для сферической многослойной стены.
Здесь D 1 и D 2 – внутренний и внешний диаметры стенки, D – опорный диаметр, по которому определяется эталонная поверхность теплообмена, S i , D i , D i+1 и λ i — толщина, внутренний и внешний диаметры, теплопроводность i-го слоя. Первое и третье слагаемые в скобках называются термическими сопротивлениями теплопередачи. Для их снижения стенки ребрятся и используются различные способы увеличения теплоотдачи. Второе слагаемое в скобках означает термическое сопротивление стены, которое может значительно увеличиться в результате загрязнения стены, например, отложениями накипи и золы, или плохой теплопередачей между слоями стены. Значения α и U для малого элемента поверхности теплообмена называются локальными. Если они не сильно различаются, то при практических расчетах теплообмена на поверхностях конечных размеров используются средние значения коэффициентов и уравнение теплопереноса
где A — эталонная поверхность теплопередачи и (часто среднее логарифмическое) падение температуры (см.
« Средняя разница температур» ).
Таблица 1. Приблизительные значения коэффициента теплопередачи
Schneider, P.J. (1955) Кондуктивная теплопередача , Addison-Wesley Publ. Ко, Кембридж.
Адьютори, Э. Ф. (1974) Новая теплопередача, тома. 1,2, Ventuno Press, Цинциннати.
Каталожные номера
- Джейкоб М. (1958) Heat Transfer , Wiley, New York, Chapman and Hall, London.
- Schneider, P.J. (1955) Conductive Heat Transfer , Addison-Wesley Publ. Ко, Кембридж.
- Adiutory, EF (1974) The New Heat Transfer, тт. 1,2, Ventuno Press, Цинциннати.
коэффициент теплопередачи
коэффициент теплопередачи в термодинамике, машиностроении и химическом машиностроении используется для расчета теплопередачи, как правило, путем конвекции или фазового перехода между жидкостью и твердым телом:
где
- Q = тепловложение или теплопотери, Дж
- ч = общий коэффициент теплопередачи, Вт/(м 2 К)
- А = площадь поверхности теплообмена, м 2
- Δ T = разница температур между твердой поверхностью и окружающей жидкостью, K
- Δ t = период времени, с
Из приведенного выше уравнения коэффициент теплопередачи является коэффициентом пропорциональности между тепловым потоком, Q /( AΔt ), и термодинамической движущей силой для потока тепла (т.
е. разностью температур, ΔT ).
Коэффициент теплопередачи выражается в единицах СИ в ваттах на метр в квадрате-кельвин (Вт/(м 2 К)).
Коэффициент теплопередачи можно рассматривать как обратную величину теплового сопротивления.
Существует множество соотношений для расчета коэффициента теплопередачи при различных режимах теплообмена, различных средах, режимах течения и при различных теплогидравлических условиях. Часто его можно оценить, разделив теплопроводность конвекционной жидкости на шкалу длины. Коэффициент теплопередачи часто рассчитывается по числу Нуссельта (безразмерное число).
Дополнительные рекомендуемые знания
Содержимое
|
Корреляция Диттуса-Больтера
Распространенной и особенно простой корреляцией, полезной для многих приложений, является корреляция теплопередачи Диттуса-Болтера для жидкостей в турбулентном потоке.
Эта корреляция применима, когда принудительная конвекция является единственным способом передачи тепла; т. е. нет кипения, конденсации, значительного излучения и т. д. Ожидается, что точность этой корреляции составит +/-15%.
Для жидкости, текущей в прямой круглой трубе с числом Рейнольдса от 10 000 до 120 000 (в диапазоне турбулентного течения в трубе), когда число Прандтля жидкости составляет от 0,7 до 120, для места, удаленного от входа в трубу ( более 10 диаметров трубы; более 50 диаметров по данным многих авторов [1] ) или других возмущений потока, а при гидравлически гладкой поверхности трубы можно выразить как:
где
- k w = теплопроводность воды
- D H = гидравлический диаметр
- Nu = число Нуссельта
- = => корреляция Диттуса-Больтера
- Pr = число Прандтля =
- Re = число Рейнольдса =
- = массовый расход
- μ = вязкость жидкости
- C p = теплоемкость при постоянном давлении
- A = площадь поперечного сечения потока
- n = 0,4 для нагрева (стенка горячее, чем объемная жидкость) и 0,3 для охлаждения (стенка холоднее, чем объемная жидкость) [2] .
Свойства жидкости, необходимые для применения этого уравнения, оцениваются при объемной температуре, что позволяет избежать итераций.
Коэффициент теплопередачи стенки трубы
Сопротивление тепловому потоку материала стенки трубы можно выразить как «коэффициент теплопередачи стенки трубы». Однако необходимо выбрать, основан ли тепловой поток на внутреннем или внешнем диаметре трубы.
Выбирая основу для теплового потока на основе внутреннего диаметра трубы и предполагая, что толщина стенки трубы мала по сравнению с внутренним диаметром трубы, тогда можно рассчитать коэффициент теплопередачи для стенки трубы, как если бы стенка не была искривленной :
где k — эффективная теплопроводность материала стенки, t — толщина стенки.
Если приведенное выше предположение не выполняется, то коэффициент теплопередачи стенки можно рассчитать, используя следующее выражение:
где d i и d o — внутренний и наружный диаметры трубы соответственно.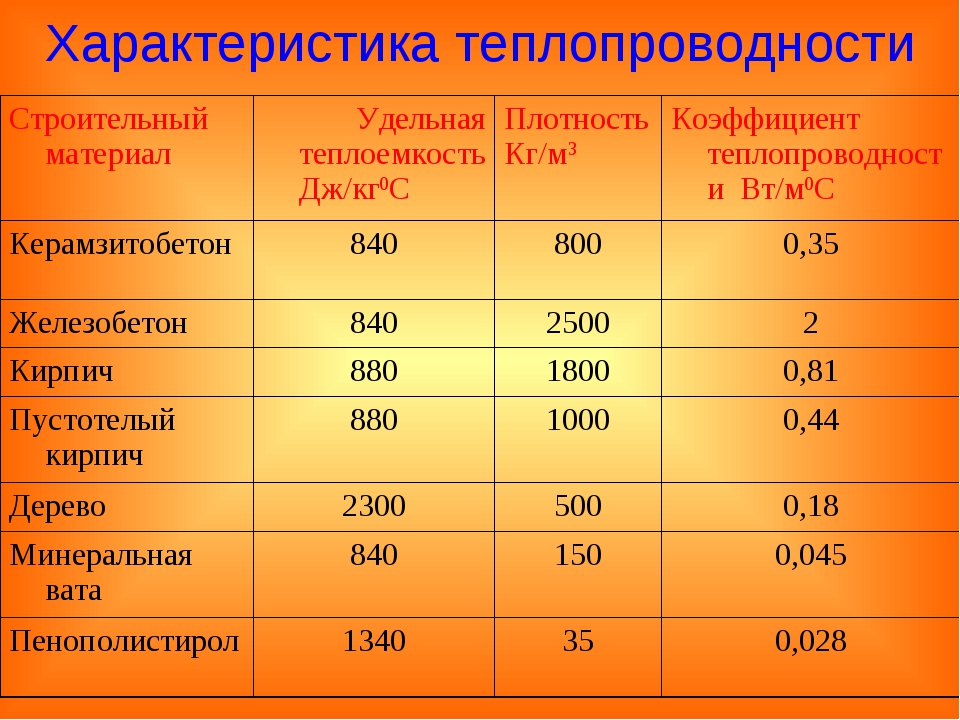
Теплопроводность материала трубы обычно зависит от температуры; часто используется средняя теплопроводность.
Комбинация коэффициентов теплопередачи
Для двух или более процессов теплопередачи, действующих параллельно, коэффициенты теплопередачи просто складываются:
Для двух или более процессов теплопередачи, соединенных последовательно, коэффициенты теплопередачи складываются обратно пропорционально. Это означает, что общий коэффициент теплопередачи представляет собой гармоническое среднее частных коэффициентов теплопередачи:
Например, рассмотрим трубу, внутри которой течет жидкость. Скорость теплопередачи между объемом жидкости внутри трубы и внешней поверхностью трубы составляет:
где
- Q = мощность теплопередачи (Вт)
- h = коэффициент теплопередачи (Вт/м 2 .K)
- t = толщина стены (м)
- k = теплопроводность стены (Вт/м.
