Расчет перемычек: Как подобрать перемычки в кирпичных стенах

Как подобрать перемычки в кирпичных стенах

В кирпичной кладке над оконными и дверными проемами необходимо укладывать перемычки — обычно это железобетонные элементы заводского изготовления по типовой серии 1.038.1-1 или в случае больших пролетов — по серии 1.225-2. Также, если нет возможности купить готовые перемычки, можно в условиях стройки выполнить армированные монолитные железобетонные перемычки или балки из металлических элементов — все зависит от размеров проема и нагрузки на стену.

Железобетонные перемычки по серии 1.038.1-1

. Подобрать перемычки по данной серии просто. Нужно знать:

— ширину проема,

— нагрузку на перемычку от собственного веса, веса стены и перекрытия (обычно для жилых домов, в которых нет больших нагрузок, можно выделить три типа: 1 — случай, когда на стену опирается перекрытие; 2 — когда стена самонесущая и перекрытие не опирается; 3 — когда перемычка укладывается в кирпичной перегородке толщиной 120 мм).

Все перемычки в серии имеют обозначение, например 2ПБ18-8 и приведены в виде таблицы, в которой указаны необходимые характеристики — размеры, вес и допустимая нагрузка на перемычку.

Что зашифровано в названии перемычки 2ПБ18-8?

ПБ — это марка. Есть марка ПБ — перемычки брусковые шириной 120 или 250 мм, которые нужно набирать по несколько штук в зависимости от ширины стены и толщины перемычки (для перегородки толщиной 120 мм укладывается одна перемычка, для стены толщиной 380 мм — уже две или три перемычки). А есть марка ПП — это перемычки плитные шириной 380 или 510 мм, рассчитанные на то, чтобы перекрыть сразу всю стену по ширине.

2 — это шифр, скрывающий в себе размеры сечения перемычки. Так перемычка с шифром 1ПБ имеет сечение 120х65 мм, где 120 мм — это ширина перемычки; шифр 2ПБ — 120х140 мм; шифр 3ПБ — 120х220 мм; шифр 4ПБ — 120х290 мм; шифр 5ПБ — 250х220 мм (250 мм — ширина). Для плитных перемычек свои значения. Все это можно посмотреть в таблицах серии 1. 038.1-1.

18 — в этом шифре заложена длина перемычки 1810 мм. Если вычесть глубину опирания на стену с двух сторон по 100 мм, получим максимальную ширину проема для данной перемычки 1610 мм.

8 — это нагрузка, которую перемычка выдерживает (в данном случае 800 кг/м). Например, если это 8, то перемычка отлично справится с самонесущей стеной, если 1 — это только для перегородок, а начиная с 27 и выше можно применять для стен, на которые опирается перекрытие.

Как просто подобрать перемычку по серии 1.038.1-1? Разберем на примерах:

Пример 1. Проем в кирпичной перегородке толщиной 120 мм размером 900 мм. Кладка в летних условиях.

Нагрузка на такую перемычку небольшая, для перегородок подходят три типа перемычек:

1ПБ10-1 (длиной 1030 мм), 1ПБ13-1 (длиной 1290 мм) и 1ПБ16-1 (длиной 1550 мм). Минимальная глубина опирания перемычки на стену 100 мм.

Определим длину перемычки: 900 + 100 + 100 = 1100. Таким образом, нам подходит перемычка длиной 1290 мм марки 1ПБ13-1.

Другие примеры подбора перемычке в перегородках здесь.

Пример 2. Самонесущая стена (перекрытие на нее не опирается) толщиной 250 мм, над проемом высота стены 900 мм, проем размером 1400 мм. Кладка в зимних условиях.

Так как ширина стены 250 мм, перемычек нужно две по ширине стены.

В зимних условиях на самонесущую перемычку берется нагрузка от высоты стены, равной расчетному пролету перемычки. Предварительно принимаем расчетный пролет равным 1400 + 2*100/3 = 1470 мм (здесь 100 мм — глубина опирания перемычки). Т.к. 1470 мм > 900 мм (высоты кладки над перемычкой), то в расчете будет участвовать величина 900мм.

Определим нагрузку на 1 погонный метр перемычки:

0,25*0,9*1,8*1,1/2 = 0,23 т/м = 230 кг/м (здесь 1,8 т/м3 — вес кирпича, 1,1 — коэффициент надежности, 2 – количество перемычек), при этом собственный вес перемычки еще не был добавлен. С учетом того, что нужно будет учесть собственный вес перемычки, выберем нагрузку в таблице серии 300 кг/м. Выбираем перемычку с индексом 3. Для этих перемычек минимальная глубина опирания 100 мм.

Определим наименьшую возможную длину перемычки: 1400 + 100 + 100 = 1600 мм.

Подбираем перемычку длиной 1940 мм 2ПБ19-3.

Нагрузка от собственного веса этой перемычки равна 81/1,94 = 42 кг/м, таким образом, несущей способности 300 кг/м достаточно, чтобы выдержать нагрузку, равную 230 + 42 = 272 кг/м.

Еще примеры подбора перемычек в самонесущих стенах здесь.

Пример 3. Несущая стена толщиной 380 мм с опиранием перекрытия пролетом 3 м с одной стороны, над проемом высота стены 900 мм, проем размером 1350 мм. Кладка в летних условиях.

Для этого варианта нужно подобрать две разные перемычки — несущую со стороны опирания перекрытия и менее мощную с другой стороны. Чем больше несущая способность перемычки, тем она дороже.

При кладке в летних условиях нагрузка от перемычки берется от 1/3 расчетного пролета перемычки. Но для несущей перемычки берется вся высота кладки — от верха перемычки до низа перекрытия, т. е. нагрузку будем рассчитывать от высоты 900 мм. А вот для ненесущей перемычки предварительно примем расчетный пролет равным 1350 + 2*100/3 = 1420 мм, тогда 1420/3 = 470 мм — высота кладки, от которой определим нагрузку для ненесущей перемычки.

Определим нагрузку на 1 погонный метр стены со стороны опирания перекрытия:

1,1*0,3*0,5*3 + 1,2*0,15*0,5*3 + 0,66*1,1*1,8*0,38*0,9 = 1,21 т/м = 1210 кг/м (здесь 1,1 и 1,2 — коэффициенты, 0,3 — нагрузка от 1 кв. м перекрытия, 0,5*3 — половина пролета перекрытия, 0,15 — временная нагрузка, 0,66*1,1*1,8*0,38*0,9 — две трети нагрузки от веса стен, определяется как в примере 2). Ближайшая большая нагрузка в таблицах серии 2800 кг/м. Выбираем перемычку с индексом 27. Для этих перемычек минимальная глубина опирания 230 мм, ширина перемычки 250 мм.

Определим наименьшую возможную длину перемычки: 1350 + 230 + 230 = 1810 мм.

Подбираем перемычку длиной 1810 мм 5ПБ18-27. Нагрузка от веса этой перемычки равна 250/1,81 = 138 кг/м, итого нагрузка на перемычку 1210 + 138 = 1348 кг/м, что значительно меньше допустимой нагрузки 2800 кг/м – прочность обеспечена.

Нагрузка на 1 погонный метр стены со стороны, на которую перекрытие не опирается равна:

0,33*1,1*1,8*0,38*0,47 = 0,117 т/м = 117 кг/м (здесь 0,33 — 1/3 ширины стены). Ближайшая большая нагрузка 250 кг/м.

Выбираем перемычку с индексом 2, для нее глубина опирания 100 мм.

Определим наименьшую возможную длину перемычки: 1350 + 100 + 100 = 1550 мм.

Максимальная длина перемычек с индексом 2 равна 1480 мм, что меньше требуемой. Подбираем наиболее подходящую перемычку 2ПБ19-3 (длиной 1940 мм) или 3ПБ18-8 (длиной 1810 мм). Если добавить к полученной нагрузке 223 кг/м собственный вес любой из выбранных перемычек, мы убедимся, что их несущей способности достаточно.

Другие примеры подбора перемычек в несущих стенах можно найти здесь.

Пример 4. Несущая стена толщиной 380 мм с опиранием перекрытия пролетом 6 м с одной стороны и 4,2 м с другой, над проемом высота стены 900 мм, проем размером 1200 мм. Кладка в зимних условиях.

В зимних условиях нагрузка берется от части стены, высота которой равна расчетному пролету перемычки. Т.к. ширина проема 1200 мм больше высоты стены над проемом 900 мм, то в расчете будет участвовать величина 900 мм.

Определим нагрузку на 1 погонный метр:

1,1*0,3*5,1 + 1,2*0,15*5,1 + 0,68 = 3,3 т/м = 3300 кг/м (здесь 1,1 и 1,2 — коэффициенты, 0,3 — нагрузка от 1 кв. м перекрытия, 5,1 = (6+4,2)/2 м — длина сбора нагрузки от перекрытия, 0,15 — временная нагрузка, 0,68 = 0,38*0,9*1,8*1,1 т/м — нагрузки от веса стены).

Подберем плитную перемычку. Нагрузка на нее без учета собственного веса 3300 кг/м.

Ближайшая большая нагрузка 7200 кг/м. Выбираем перемычку с индексом 71. Минимальная глубина опирания для таких перемычек 170 мм.

Определим длину перемычки: 1200 + 170 + 170 = 1540 мм. Подбираем плитную перемычку 3ПП16-71 длиной 1550 мм.

Скачать серии железобетонных перемычек можно здесь:

Серия 1.038.1-1, выпуск 1 «Перемычки брусковые для жилых и общественных зданий»

Серия 1.038.1-1, выпуск 2 «Перемычки плитные для жилых и общественных зданий.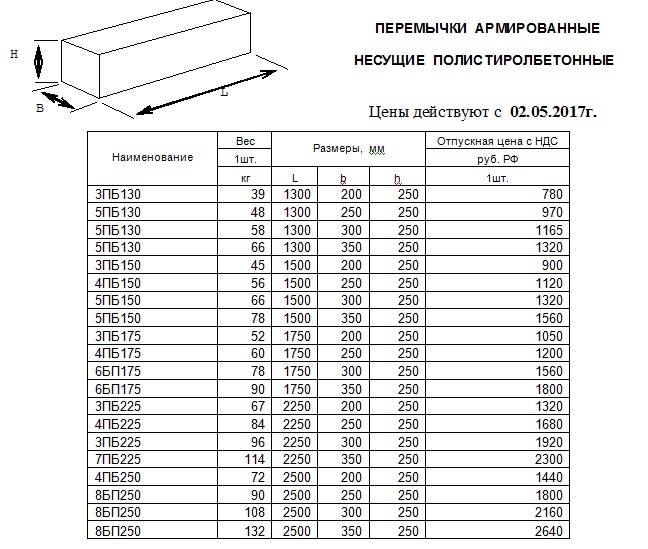 Рабочие чертежи»

Серия 1.038.1-1 Перемычки железобетонные вып.4

Серия 1.038.1-1 Перемычки железобетонные для зданий с кирпичными стенами Выпуски 3,5-13

И напоследок, цитата из СНиП «Каменные и армокаменные конструкции» (для тех, кто подходит к вопросу подбора перемычек более тщательно:

Еще статьи на тему перемычек:

Как подобрать перемычки в частном доме — примеры расчета.

«Подбираем перемычки в кирпичных перегородках – примеры расчета. Проемы №1-3.»

Подбираем перемычки в самонесущих кирпичных стенах — примеры расчета. Проемы №4-6.

Подбираем перемычки в несущих кирпичных стенах — примеры расчета. Проемы №7-11.

Как выполнить чертеж перемычек — схему перекрытия оконных и дверных проемов

Устройство металлической перемычки

Еще полезные статьи:

«Выбор материала для стен»

«Расчет кладки из газобетона на смятие под действием нагрузки от перекрытия.»

«Как рассчитать стены из кладки на устойчивость. »

«Как пробить проем в существующей стене.»

Расчет железобетонных перемычек. Виды железобетонных перемычек.

Содержание:

• Расчет железобетонных перемычек.
• Виды железобетонных перемычек.
• Как подбирать железобетонные перемычки.
• Заключение.
• Полезная информация:

При возведении кирпичных стен неизбежно возникает необходимость установки над оконным проемом железобетонной перемычки. Они представляют собой железобетонные балки с различным сечением и длиной, изготовленные на заводе. Чтобы выбрать необходимый типоразмер изделия, необходимо произвести предварительные расчеты, которые будут учитывать такие данные как нагрузка на перемычку и ширина проема. Расчет железобетонных перемычек.

При этом, говоря о нагрузке, имеют в виду собственный вес перемычки суммарно с весом стены и перекрытия. В случае с жилыми домами, где нагрузки не так высоки, все случаи принято разбивать на три группы:

1. На стену опирается перекрытие.
2. Перекрытие на стену не опирается, а сам она является самонесущей.
3. Перемычку укладывают в перегородке из кирпича толщиной 12 см.

Виды железобетонных перемычек.

Прежде чем приступить к расчетам, давайте немного ознакомимся с видами самих перемычек. Чтобы понимать, какие варианты вам доступны, следует открыть сайт любого производителя ЖБИ и посмотреть, какие виды перемычек железобетонных присутствуют в их номенклатуре. Перейдя по ссылке, вы увидите длинный список типоразмеров с их характеристиками. Чтобы научиться быстро ориентироваться в нем, следует научиться расшифровывать маркировку. Сделаем это на примере перемычки 2ПБ 16-2:

• 2ПБ – эта часть маркировки означает принадлежность изделия к какому-то виду и типу сечения. В данном случае – перемычка брусковая второго типа сечения.
  • Брусковые перемычки (ПБ) могут иметь ширину 120 или 250 мм, что делает необходимым использование сразу нескольких изделий в случаях, когда толщина перегородки превышает 120 мм. Производят также плитные перемычки (ПП), ширина которых бывает 380 и 510 мм.
  • Второй тип сечения (2ПБ) имеет размеры 120х140 мм. Другие типы имеют следующие габариты: 1ПБ – 120х65 мм, 3ПБ – 120х220 мм, 4ПБ – 120х290 мм, 5ПБ – 50х220 мм.
• 16 – эта часть шифра говорит о длине изделия, которая равняется 1550 мм. Размер выражен в дециметрах и округлен.
• 2 – последняя цифра условного обозначения означает нагрузку, на прием которой рассчитана перемычка. В данном случае это 200 кг/м. Приблизительно понимать эти данные следует так: перемычки с индексом нагрузки 1 обычно используют для перегородок; индекс 8, говорит о том, что такие изделия с легкостью справляются с самонесущими стенами; индексом 27 обладают перемычки, применяемые в стенах, на которые опираются перекрытия.

Теперь, зная разнообразие железобетонных перемычек, можно переходить непосредственно к расчету.

Как подбирать железобетонные перемычки.

Расчет железобетонных перемычек. Итак, давайте сперва введем какие-то исходные данные. Допустим, нам надо рассчитать, какую перемычку следует брать для перекрытия пролета шириной 1350 мм в самонесущей стене толщиной 240 мм при высоте стены над проемом – 800 мм. Стройка ведется в зимних условиях.

Толщина стены 240 мм говорит о том, что нам понадобятся две брусковые перемычки шириной по 12 мм. В зимний период на самонесущую перемычку берут нагрузку от высоты стены, равной расчетному пролету. Расчетный пролет считается так:

1350 + 2*100/3 = 1420 мм

100 мм в данном случае – это минимальная глубина опирания перемычки. Так как высота кладки оказалась меньше расчетного пролета, в дальнейшем в расчетах будем использовать именно ее – 800 мм.

Далее определяем нагрузку на 1 погонный метр изделия:

0,24*0,8*1,8*1,1/2  = 0,19 т/м = 190 кг/м

В этих расчетах 1,8 т/м3 – это вес кирпича, 1,1 – коэффициент надежности, 2 – количество перемычек. Итак, нам необходимо выбирать перемычку из тех, чей индекс нагрузки не менее 2-х.

Как мы уже говорили выше, минимальная глубина опирания данных перемычек составляет 10 см, значит наименьшая возможная длина перемычки в нашем случае равна:

1350 + 100*2 = 1550 мм

Из списка типоразмеров нам могла бы подойти перемычка 2ПБ 16-2 длиной как раз 1550 мм и расчетной нагрузкой до 200 кг/м. Однако нам еще следует учесть нагрузку от собственного веса балки, которая равна 70/1,55 = 45 кг/м. То есть суммарная нагрузка будет составлять 190 + 45 = 235 кг/м, что превышает максимально допустимую для данной перемычки.

В нашем случае подойдет перемычка 2ПБ 19-3. Собственная нагрузка для нее составляет 80/1,94 = 41 кг/м. Тогда суммарная будет равна 190 + 41 = 231 кг/м, что не превышает допустимые 300 кг/м для этой балки. Длина перемычки составляет 1940 мм, и это тоже подходит для наших условий.

Заключение.

Приведенный пример основан на конкретных данных, которые могут значительно отличаться в зависимости от изменяющихся условий. В отдельных случаях должны учитываться другие дополнительные данные. Например, длина перекрытия пролетом или летний период строительства. Все это будет отражаться на расчетах, но базовый принцип, изложенный в этой статье, является их основой.

Расчет силы вертикального прыжка

Тесты на вертикальный прыжок обычно записываются как пройденное расстояние в сантиметрах или дюймах. Это не всегда говорит о полной истории. Более тяжелому человеку, прыгающему на ту же высоту, что и более легкому, приходится совершать гораздо большую работу, чтобы переместить большую массу. Поэтому иногда бывает полезно преобразовать оценку в единицы мощности или работы.

Механическая работа, выполняемая для совершения вертикального прыжка, может быть определена с использованием измеренного расстояния высоты прыжка (работа = сила x расстояние, где сила = масса x ускорение). Однако Власть не может
вычислить (мощность = работа/время), поскольку время действия силы на тело неизвестно. Мощность можно измерить напрямую с помощью силовой пластины, хотя они не всегда доступны. Со временем было разработано несколько различных формул, которые оценивают силу на основе измерений вертикального прыжка. Некоторые из них представлены ниже с примерами.

Во всех приведенных ниже примерах используется гипотетический вертикальный прыжок на 60 см (0,6 метра или 23,5 дюйма) человеком весом 75 кг и ростом 180 см. Как видите, достигнуты совершенно разные результаты. Отчасти это связано с тем, что не всегда ясно, оценивается ли пиковая мощность или средняя мощность.

Формула Льюиса

Формула Льюиса или номограмма (Fox & Mathews, 1974) является широко используемой формулой (найдена во многих учебниках для средней школы). Эта формула оценивает только среднюю мощность и основана на модифицированном уравнении падающего тела. В исходной формуле использовались единицы кг·м·сек-1. Чтобы преобразовать его в ватты, стандартную единицу мощности, умножьте на 9..81 был добавлен.

Средняя мощность (Ватт) = √ 4,9 x масса тела (кг) x √ показатель вылета в прыжке (м) x 9,81 

Пример

• Средняя мощность =
  (квадратный корень из 4,9) x масса тела (кг) x (квадратный корень из расстояния прыжка (м)) x 9,81
• Средняя мощность = 2,2136 х 75 х 0,7746 х 9,81
• Средняя мощность = 1261,6 Вт

Формула Harman

Чтобы устранить ограничения формулы Льюиса, Harman et al. (1991) установлены уравнения для
как пиковую, так и среднюю мощность с помощью нескольких процедур регрессии. Два уравнения
перечислены ниже. В первом уравнении это может быть -1,822 вместо + 1,822 , см. комментарии ниже.

Пиковая мощность (Вт) = 61,9 · высота прыжка (см) + 36,0 · масса тела (кг) + 1,822

Средняя мощность (Вт) = 21,2 · высота прыжка (см) + 23,0 · масса тела (кг) – 1,393

Примеры

• Пиковая мощность (Вт) = (61,9 х высота прыжка (см)) + (36 х масса тела (кг)) + 1822
• Пиковая мощность (Вт) = (61,9 х 60) + (36 х 75) + 1822
• Пиковая мощность (Вт) = 3714 + 2700 + 1822
• Пиковая мощность (Вт) = 8236 Вт
• Средняя мощность (Вт) = (21,2 х высота прыжка (см)) + (23,0 х масса тела (кг)) – 1393
• Средняя мощность (Вт) = (21,2 х 60) + (23 х 75) — 1393
• Средняя мощность (Вт) = 1272 + 1725 — 1393
• Средняя мощность (Вт) = 1604 Вт

Джонсон и Бахамонд Формула

Джонсон и Бахамонд
(1996) также разработали формулу для расчета пиковой и средней мощности в тесте вертикального прыжка с использованием прыжка в обратном направлении. В этих уравнениях используется дополнительный фактор роста.

Пиковая мощность (Вт) = 78,6 · VJ (см) + 60,3 · масса (кг) — 15,3 · высота (см) — 1,308

Средняя мощность (Вт) = 43,8 · VJ (см) + 32,7 · масса (кг) — 16,8 · высота (см) + 431

Примеры

• Пиковая мощность (Вт) = (78,6 x VJ (см)) + (60,3 x масса (кг)) — (15,3 x высота (см)) -1308
• Пиковая мощность (Вт) = (78,6 х 60) + (60,3 х 75) — (15,3 х 180) — 1308
• Пиковая мощность (Вт) = 4716 + 4522,5 — 2754 — 1308
• Пиковая мощность (Вт) = 5176,5 Вт
• Средняя мощность (Вт) = (43,8 x VJ (см)) + (32,7 x масса (кг)) — (16,8 x высота (см)) + 431
• Средняя мощность (Вт) = (43,8 х 60) + (32,7 х 75) — (16,8 х 180) + 431
• Средняя мощность (Вт) = 2628 + 2452,5 — 3024 + 431
• Средняя мощность (Вт) = 2487,5

Формула Sayers

Уравнение Sayers (Sayers et al. 1999) также оценивает пиковую выходную мощность (пиковую анаэробную выходную мощность или
PAPw) от вертикального прыжка.

PAPw (Ватт) = 60,7 · высота прыжка (см) + 45,3 · масса тела (кг) — 2055

Пример

• PAPw = (60,7 x высота прыжка (см)) + (45,3 x масса тела (кг)) — 2055
• PAPw = (60,7 х 60) + (45,3 х 75) — 2055
• PAPw = 3642 + 3397,5 — 2055
• PAPw = 4984,5 Вт

Формула Bosco

Была определена формула для измерения средней мощности теста Bosco с повторным вертикальным прыжком. Средняя генерируемая мощность (Вт) рассчитывается исходя из продолжительности испытания (Ts от 15 до 60 с), количества прыжков (n), общего времени полета (Ft) и где g — ускорение свободного падения, так что;

W = (Ft Ts g2) / 4n (Ts — Ft)

Другое

Я также встречал эту формулу для расчета мощности от высоты вертикального прыжка. Эта формула до недавнего времени использовалась на Комбинате НХЛ.

Мощность (фут-фунт/сек) = 4 x вес (фунт) x
√ высота прыжка (футы)

Ссылки

• Bosco C, Luhtanen P, Komi PV (1983) Простой метод измерения механической силы в прыжках . Европейский журнал прикладной физиологии 50:273-282.
• Harman, E.A., Rosenstein, MT, Frykman, P.N., Rosenstein, R.M., and Kraemer, WJ
  (1991). Оценка выходной мощности человека при вертикальном прыжке . Журнал
  Прикладные спортивные исследования, 5(3), 116-120.
• Джонсон, Д.Л., и Бахамонд, Р. (1996). Оценка выходной мощности в университете
  Спортсмены. Journal of Strength and Conditioning Research, 10(3), 161-166.
• Кейр, П.Дж., В.К. Джамник и Н. Гледхилл. (2003) Технико-методологический отчет: Номограмма пиковой выходной мощности ног в вертикальном прыжке , Журнал исследований силы и физической подготовки Том: 17 Выпуск: 4 Страницы: 701-703.
• Sayers, S., et al. (1999) Перекрестная проверка трех уравнений мощности прыжка. Медицинские спортивные упражнения . 31: 572.

Связанные страницы

• Расчет мощности во время работы
• Физика вертикального прыжка
• Процедура тестирования вертикального прыжка и использование метода хронометража
• Результаты теста вертикального прыжка.
• Преобразование единиц вертикального перехода между сантиметрами и дюймами.
• Устройства для вертикального прыжка в магазине фитнес-тестирования.
• О силовых плитах

Старые комментарии

Комментирование закрыто на этой странице, хотя вы можете прочитать некоторые предыдущие комментарии ниже, которые могут ответить на некоторые ваши вопросы.

• Если мы конвертируем ватты в кг/метры/сек, это даст нам (в кг/метры секунд) 
  (a) Lewis: 128
  (b) Harman:peak839-avrg163
  (c) Johnson&Bahamonde:peak527 -avrg253
  (d) Sayers : 508
  Значит, спортсмен должен поднять в «жиме ногами» вышеуказанные результаты, в кг.
  Если мое «отношение/уравнение» верно, это означает, что только формула ЛЬЮИСа может быть действительной.
  (из Geo, июнь 2022 г.)
• Вертикальные прыжки являются составной частью большинства видов спорта. Часто считается само собой разумеющимся, что спортсмен инстинктивно умеет прыгать вертикально. На самом деле, вертикальные прыжки — это навык, которому можно и нужно обучать спортсменов. Исследования доказали, что тяжелая атлетика и плиометрические тренировки эффективно улучшают выходную мощность. Комбинация обоих может привести к улучшению вашего вертикального прыжка.
  Мишель Бивенс (2013)
• Я не силен в математике, так что может кто-нибудь сказать мне, если у моего сына 46-дюймовая вертикаль, во сколько футов это конвертируется. Джозеф Барнс (2019)
• привет. спасибо за все мысли. но я не смог найти нормы номограммы Льюиса. Вы можете помочь мне? Дженгиз Олмез (2018)
• Хотелось бы узнать, какая будет единица мощности, если не добавить 9,81? И не могли бы вы помочь мне с тестом верхней конечности с замкнутой кинетической цепью для верхней конечности. .. в какой единице он дает оценку мощности?? Михаил (2013)
• Вы уверены, что уравнение Хармана равно +1822, а не -1822. Колин (2013)
  • Роб Админ Колин (2013)
    глядя на исходную статью, в которой указано +1822, даже несмотря на то, что она кажется завышенной по сравнению с другими перечисленными уравнениями.
  • Колин Роб (2013)
    Я знаю, я тоже это видел… но в статье Сэйерса (которая включает Хармана в качестве одного из исследователей) используется -1822…
  • Я упомянул об этом просто потому, что в моей статье уравнение Хармана дает очень большую пиковую выходную мощность по сравнению со всеми другими формулами… и я нашел много исследовательских работ, в которых также используется -1822
  • Но, возможно, уравнение Хармана неверно из-за малого размера выборки (n=17)… в любом случае, спасибо за информацию
  • Колин Роб (2013)
    Привет, Роб, я могу ошибаться. Я всего лишь студент, который пытается написать исследовательскую работу о вертикальном прыжке с помощью Vertec® и силовых платформ. .. и формула Хармана полностью отбрасывает его. -1822 приблизит данные к другим формулам, и я обнаружил, что +1822 полностью завышает… но до сих пор не могу найти окончательный ответ… буду очень признателен за любую имеющуюся у вас информацию…
• привет спасибо за информацию. у меня к вам вопрос: как вы упомянули в начале, «более тяжелый человек, прыгающий на ту же высоту, что и более легкий, должен совершить гораздо больше работы, чтобы переместить большую массу. Поэтому иногда полезно перевести счет в единицы сила или работа». скажем, 2 человека весят 75 кг/180 см с вертикальным прыжком 60 см, однако у 1 человека 10% жира, а у другого 30%. если я хочу знать, какая сила им нужна для прыжка до 80 см, какая формула работает лучше всего? Спасибо за ваше время! J11 (2013)
• Сила каждого человека для прыжка на 60 см будет одинаковой, но для человека с более высоким уровнем жира в организме (и, следовательно, меньшей мышечной массой) это будет гораздо более впечатляющее усилие. Что касается лучшей формулы для использования, я понятия не имею. Просто прыжки J11 (2013)

Расчет зазора между перемычками линии электропередачи и расчет минимального угла линии

Чтобы обеспечить электрические зазоры в тупиковых конструкциях линии электропередачи, иногда требуются опоры для перемычек, такие как горизонтальные стойки или изоляторы двутавровой струны, опирающиеся на рычаги шлюпбалки, чтобы держите перемычку подальше от конструкции. Чаще всего они требуются для линейных тупиков (сооружений без линейных углов) или тупиков с малыми линейными углами; в то время как конструкции с большими углами линий, такие как показанные на рисунке 1, не требуют поддержки перемычек, поскольку только длина изоляторов обеспечивает достаточное расстояние смещения от конструкции.

В этом посте представлены уравнения, помогающие оценить зазор между перемычкой и опорой с опорами для перемычек и без них. Кроме того, будет представлено уравнение для расчета минимального угла линии, необходимого для поддержания электрических зазоров до опоры для конструкции без опоры перемычек, поскольку это значение может быть полезным при принятии общих проектных решений или определении ограничений для конструкций в рамках проекта. стандарты.

Рисунок 1: Структура без поддержки перемычек

Расстояние до конструкции без опоры перемычки

Упрощенная геометрия в плане конструкции без опоры перемычки показана на рис. 2. Показаны следующие переменные:

• $C=$ зазор между перемычкой и опорой.
• $I=$ горизонтальное смещение креплений изолятора от опоры.
• $P=$ радиус полюса в интересующей позиции.
• $\Delta=$ угол отклонения линии.

Рис. 2: Расстояние до конструкции без поддержки перемычки

На этом рисунке предполагается, что перемычка проходит по прямой линии между креплениями изолятора на правых концах сегментов $I$. Для коротких перемычек это, вероятно, консервативно, даже если учитывать разрыв провода, поскольку, скорее всего, деформационные зажимы или клеммы перемычек на концах перемычек установлены таким образом, что оборудование отводит перемычку от конструкции и обеспечивает достаточную жесткость. для предотвращения сдувания провода в сторону столба. В случае, если выброс перемычки в сторону конструкции является конструктивной проблемой, например, в случае длинных перемычек, могут быть добавлены дополнительные буферы для требуемого зазора. Кроме того, в случае крутых уклонов, когда изоляторы наклонены вниз, расстояние, используемое для $I$, должно быть горизонтальным смещением точки крепления изолятора, а не полной длиной изолятора.

Исходя из этой простой геометрии, расстояние $C$ до конструкции можно рассчитать как:

\[C = (P+I)\sin\bigg(\frac{\Delta}{2}\bigg) — P\]

Вероятно, минимальное расстояние до конструкции известно для данного сетевого напряжения. Следовательно, вместо расчета конкретных зазоров для всех интересующих конструкций может оказаться более полезным вычислить минимальный угол наклона линии, необходимый для поддержания требуемого зазора. Преобразование приведенного выше выражения приводит к следующему уравнению для минимального угла линии для конструкции без опоры перемычки.

\[\Delta_{min} = 2 \text{asin}\bigg(\frac{P+C}{P+I}\bigg)\]

Расстояние до конструкции с опорой-перемычкой

Упрощенная геометрия в плане конструкции с опорой-перемычкой показана на рис.