Расчет толщины плиты перекрытия железобетонной и монолитной | Статья завода БЗСК
Содержание:
- Для чего делается расчет плиты перекрытия в строительстве
- Основные данные для расчета плит перекрытия
- Виды расчетных нагрузок на плиту перекрытия
- Почему мы приводим самые простые примеры расчета железобетонных плит
Метод используется при проектировании и разработке раздела «Конструкции железобетонные» и представляет собой вычисление максимальной допустимой распределительной нагрузки на плиту для определения наименьшей и наибольшей толщины, ширины и длины детали. Расчет имеет экономическое значение с точки зрения выбора плиты по характеристикам и стоимости и технологическое значение, поскольку позволяет определить методы монтажа ЖБ конструкций с перекрытиями.
Для чего делается расчет плиты перекрытия в строительстве
В промышленном, гражданском и частном строительстве используется несколько способов перекрытия железобетонными плитами. Для правильного расчета необходимо определиться с методом монтажа и особенностями конструкции.
Для правильного расчета необходимо определиться с методом монтажа и особенностями конструкции.
Основные виды конструкций перекрытия с использованием монолитной железобетонной плиты:
- балочное применяется, когда перекрываемый пролет больше длины одной плиты, при этом учитывается тип плиты — для ребристой балки укладываются перпендикулярно ребрам, для гладкой выбирается направление, перпендикулярное направлению укладки плиты;
- безбалочное перекрытие представляет собой создание конструкции, опирающейся на несущие стены, а при значительных расстояниях на капители несущих колонн с креплением по закладным сваркой;
- кессонное перекрытие формируется за счет пересечения ребер, создающих несущую сетку с распределенной по ребрам нагрузкой;
- шарнирное бесконсольное или перекрытие с защемлением балок применяется в зависимости от расчетной нагрузки на узлы конструкции.
В проектном и частном строительстве могут возникать разные ситуации, когда уровни строения имеют разную конфигурацию. Поэтому расчет монолитной плиты перекрытия делается с поправкой на разброс параметров в виде коэффициента.
Поэтому расчет монолитной плиты перекрытия делается с поправкой на разброс параметров в виде коэффициента.
Основные данные для расчета плит перекрытия
Железобетонная плита для перекрытия этажей и проемов является несущей частью конструкции, для которой характерно распределение нагрузок по нескольким направлениям. В основе расчетов толщины и прочности лежит необходимость получить значения размеров и толщины, при которых:
- плита ляжет на опорные точки стен (балок, колонн) с необходимым для устойчивости нахлестом;
- на железобетонную конструкцию будут воздействовать нагрузки, не вызывающие критического изгиба плиты под действием веса частей конструкции и собственной массы;
- нагрузка на изгиб будет ограничена таким образом, чтобы на растяжение работала арматурная сетка, а не бетонный монолит;
- общий вес конструктивной части сооружения вместе с плитой не превышал допустимые нагрузки на основание и расположенные ниже части.

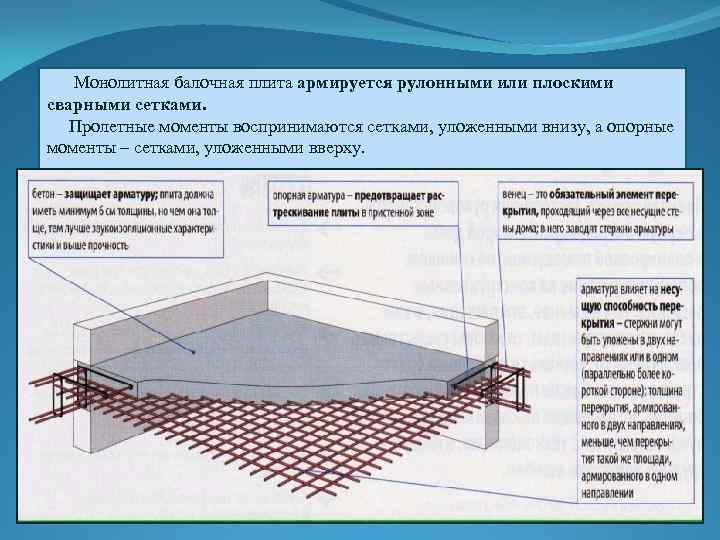
При корректном расчете можно получить результат, позволяющий подобрать готовую ЖБ плиту по размерам, весу и прочности относящуюся к одной из категорий стандартных ЖБИ. В практике современного строительства расчет монолитной плиты перекрытия делается с учетом пространственного армирования, так как подавляющее большинство изделий этого типа выпускается с применением арматуры.
Виды расчетных нагрузок на плиту перекрытия
Принято классифицировать нагрузки на плиту перекрытия как длительные, кратковременные, статические и динамические. Например , весовая нагрузка при эксплуатации строения относится к длительным (вес мебели, техники, других элементов конструкции), нагрузка от строительного оборудования и техники будет кратковременной и динамической, воздействие на плиту со стороны других деталей будет долговременным и статическим. При этом могут возникать кратковременные деформирующие воздействия при усадке здания, температурных колебаниях, от проезда транспорта.
Особенностью расчета железобетонных плит считается основной упор на распределительные нагрузки. Самый простой расчет при известных значениях будет выглядеть так: основная нагрузка 400 кг/м.кв, вес плиты 250 кг/м.кв, стяжка и конструкция пола — 100 кг/м.кв. Итого нагрузка составит 750 кг/м.кв, значит, можно подобрать плиту по размерам и прочности, применив страховочный коэффициент 1,2 на непредвиденное нагружение. Важно! — в приведенном примере расчета железобетонной плиты перекрытия указаны именно нагрузки на квадратный метр, то есть не абсолютные цифры веса каких-то предметов.
Почему мы приводим самые простые примеры расчета железобетонных плит
В практике строительства распространены стандартные ЖБ плиты. Расчет размеров и прочности для заливки монолитной плиты перекрытия без армирования и с использованием опалубки не может быть сделан на месте, без применения специальных программ. При таких вычисления необходимо учитывать сечение и тип арматуры, качество и марку прочности бетона, особенности конструкции монолитного здания.
Для того, чтобы избежать ошибок в расчетах для определения размеров и несущей способности плит перекрытия, можно выбрать один из путей:
- использовать стандартные ЖБ плиты с армированием и известными характеристиками, сделав предварительный расчет нагрузки с учетом веса плиты и деформаций;
- использовать программы для проектирования ЖБ узлов и конструкций с базой данных доступных по СНиП 52-01-2003 и СП 52-101-2003 значений и параметров.
Приводим пример расчетов плиты для пустотной плиты перекрытия для жилого помещения при размерах пролета 6 м и ширине 1,5 м. В качестве опоры используются поперечные стены здания, что делает расчет аналогичным расчету двутавровой профильной балки, свободно уложенной на две опоры.
Высота сечения многопустотной предварительно напряженной плиты по конструктивным соображениям:
h = (1/15÷1/30)l0 = 0,385÷0,19
принимаем h = 0,22м
Рабочая высота сечения:
h0 = h – as = 0,22 – 0,03 = 0,19м
Расчетная нагрузка на 1 м при ширине плиты 1,5 м с учетом коэффициента надежности по назначению здания γn = 0,95
- · постоянная q = 6,266·1,5 = 9,399 kH/м
- · временная p = 0,98 ·1,5 = 1,47 kH/м
- · полная q + p = 7,246·1,5 = 10,869 kH/м
Нормативная нагрузка на 1м
- · постоянная qn = 5,399·1,5 = 8,099 kH/м
- · временная pn = 0,7·1,5 = 1,05 kH/м
- · полная qn + pn = 6,099·1,5 = 9,149 kH/м
Если вы не располагаете опытом проектирования и выполнения расчетов для разных типов монолитных и железобетонных плит, то выполнение этой задачи будет невозможно.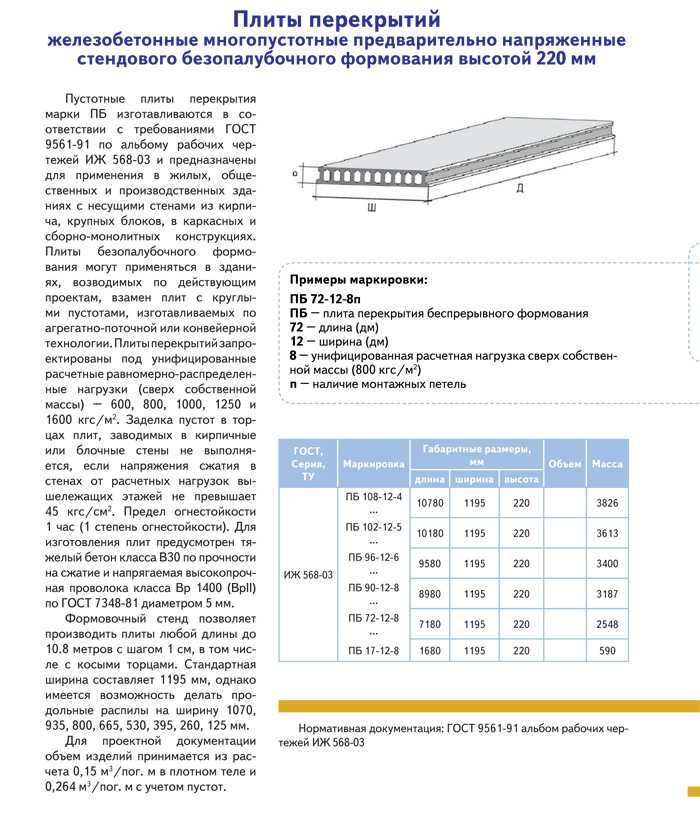 Именно поэтому в жилом строительстве отдается предпочтение готовым ЖБИ с известными параметрами.
Именно поэтому в жилом строительстве отдается предпочтение готовым ЖБИ с известными параметрами.
Расчет монолитной плиты перекрытия пример
12 апреля 2021
16202
Оглавление: [скрыть]
- Определение параметров плиты
- Расчет максимального изгибающего момента
- Сечение арматуры
- Основные параметры
- Расчет прямоугольной плиты
- Формулы и коэффициенты
- Пример варианта при конкретной ширине плиты
Частные строители в процессе возведения своего дома часто сталкиваются с вопросом: когда необходимо произвести расчет монолитной железобетонной плиты перекрытия, лежащей на 4 несущих стенах, а значит, опертой по контуру? Так, при расчете монолитной плиты, имеющей квадратную форму, можно взять в расчет следующие данные. Кирпичные стены, возведенные из полнотелого кирпича, будут иметь толщину 510 мм. Такие стены образуют замкнутое пространство, размеры которого равны 5х5 м, на основания стен будет опираться железобетонное изделие, а вот опорные площадки по ширине будут равны 250 мм.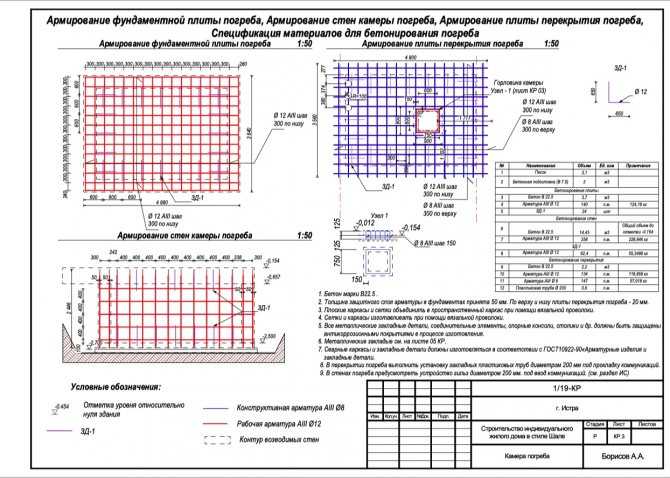 Так, размер монолитного перекрытия будет равен 5.5х5.5 м. Расчетные пролеты l1 = l2 = 5 м.
Так, размер монолитного перекрытия будет равен 5.5х5.5 м. Расчетные пролеты l1 = l2 = 5 м.
Схема армирования монолитного перекрытия.
Кроме собственного веса, который прямо зависит от высоты плиты монолитного типа, изделие должно выдерживать еще некоторую расчетную нагрузку.
Схема монолитного перекрытия по профнастилу.
Отлично, когда данная нагрузка уже известна заранее. Например, по плите, высота которой равна 15 сантиметрам, будет производиться выравнивающая стяжка на основе цемента, толщина стяжки при этом равна 5 сантиметрам, на поверхность стяжки будет укладываться ламинат, его толщина равна 8 миллиметрам, а финишное напольное покрытие будет удерживать мебель, расставленную вдоль стен. Общий вес мебели при этом равен 2000 килограммов вместе со всем содержимым. Предполагается также, что помещение иногда будет умещать стол, вес которого равен 200 кг (вместе с закуской и выпивкой). Стол будет умещать 10 человек, общий вес которых равен 1200 кг, включая стулья. Но такое предусмотреть чрезвычайно сложно, поэтому в процессе расчетов используют статистические данные и теорию вероятности. Как правило, расчет плиты монолитного типа жилого дома производят на распределенную нагрузку по формуле qв = 400 кг/кв.м. Данная нагрузка предполагает стяжку, мебель, напольное покрытие, людей и прочее.
Но такое предусмотреть чрезвычайно сложно, поэтому в процессе расчетов используют статистические данные и теорию вероятности. Как правило, расчет плиты монолитного типа жилого дома производят на распределенную нагрузку по формуле qв = 400 кг/кв.м. Данная нагрузка предполагает стяжку, мебель, напольное покрытие, людей и прочее.
Эта нагрузка условно может считаться временной, т. к. после строительства могут осуществляться перепланировки, ремонты и прочее, при этом одна из частей нагрузки считается длительной, другая — кратковременной. По той причине, что соотношения кратковременной и длительной нагрузок неизвестны, для упрощения процесса расчетов можно считать всю нагрузку временной.
Добавка в бетон для гидроизоляции.
Монтаж сборно монолитного перекрытия.
Цементный раствор: пропорции. Подробнее>>
Определение параметров плиты
Схема сборной плиты перекрытия.
По причине, что высота монолитной плиты остается неизвестной, ее можно принять за h, этот показатель будет равен 15 см, в этом случае нагрузка от своего веса плиты перекрытия будет приблизительно равна 375 кг/кв. м = qп = 0.15х2500. Приблизителен этот показатель по той причине, что точный вес 1 квадратного метра плиты будет зависеть не только от диаметра и количества примененной арматуры, но и от породы и размеров мелкого и крупного наполнителей, которые входят в состав бетона. Будут иметь значение и качество уплотнения, а также другие факторы. Уровень данной нагрузки будет постоянным, изменить его смогут лишь антигравитационные технологии, но таковых на сегодняшний день нет. Таким образом можно определить суммарную распределенную нагрузку, оказываемую на плиту. Расчет: q = qп + qв = 375 +400 = 775 кг/м2.
м = qп = 0.15х2500. Приблизителен этот показатель по той причине, что точный вес 1 квадратного метра плиты будет зависеть не только от диаметра и количества примененной арматуры, но и от породы и размеров мелкого и крупного наполнителей, которые входят в состав бетона. Будут иметь значение и качество уплотнения, а также другие факторы. Уровень данной нагрузки будет постоянным, изменить его смогут лишь антигравитационные технологии, но таковых на сегодняшний день нет. Таким образом можно определить суммарную распределенную нагрузку, оказываемую на плиту. Расчет: q = qп + qв = 375 +400 = 775 кг/м2.
Схема монолитной плиты перекрытия.
В процессе расчета следует взять во внимание, что для плиты перекрытия будет использован бетон, который относится к классу В20. Этот материал обладает расчетным сопротивлением сжатию Rb = 11.5 МПа или 117 кгс/см2. Будет применена и арматура, относящаяся к классу AIII. Ее расчетное сопротивление растяжению равно Rs = 355 МПа или 3600 кгс/см2.
При определении максимального уровня изгибающего момента следует учесть, что в том случае, если бы изделие в данном примере опиралось лишь на пару стен, то его можно было бы рассмотреть в качестве балки на 2-х шарнирных опорах (ширина опорных площадок на данный момент не учитывается), при всем при этом ширина балки принимается как b = 1 м, что необходимо для удобства производимых расчетов.
Вернуться к оглавлению
Расчет максимального изгибающего момента
Схема расчета монолитного перекрытия.
В вышеописанном случае изделие опирается на все стены, а это означает, что рассматривать лишь поперечное сечение балки по отношению к оси х будет недостаточно, так как можно рассматривать плиту, которую отражает пример, так же как балку по отношению к оси z. Таким образом, растягивающие и сжимающие напряжения окажутся не в единой плоскости, нормальной к х, а сразу в 2-х плоскостях. Если производить расчет балки с шарнирными опорами с пролетом l1 по отношению к оси х, тогда получится, что на балку будет действовать изгибающий момент m1 = q1l12/8. При всем при этом на балку с пролетом l2 будет действовать такой же момент m2, т. к. пролеты, которые отображает пример, равны. Однако расчетная нагрузка одна: q = q1 + q2, а если плита перекрытия имеет квадратную форму, то можно допустить, что: q1 = q2 = 0.5q, тогда m1 = m2 = q1l12/8 = ql12/16 = ql22/16. Это значит, что арматура, которая укладывается параллельно оси х, и арматура, укладываемая параллельно z, может быть рассчитана на идентичный изгибающий момент, при этом момент окажется в 2 раза меньше, чем для той плиты, которая опирается только на 2 стены.
При всем при этом на балку с пролетом l2 будет действовать такой же момент m2, т. к. пролеты, которые отображает пример, равны. Однако расчетная нагрузка одна: q = q1 + q2, а если плита перекрытия имеет квадратную форму, то можно допустить, что: q1 = q2 = 0.5q, тогда m1 = m2 = q1l12/8 = ql12/16 = ql22/16. Это значит, что арматура, которая укладывается параллельно оси х, и арматура, укладываемая параллельно z, может быть рассчитана на идентичный изгибающий момент, при этом момент окажется в 2 раза меньше, чем для той плиты, которая опирается только на 2 стены.
Схема кровли профнастилом.
Так, уровень максимального расчета изгибающего момента окажется равен: Ма = 775 х 52/16 = 1219.94 кгс.м. Но такое значение может быть использовано лишь при расчете арматуры. По той причине что на поверхность бетона станет действовать сжимающие напряжения в двух взаимно перпендикулярных плоскостях, то значение изгибающего момента, применимое для бетона, следующее: Мб = (m12 + m22)0.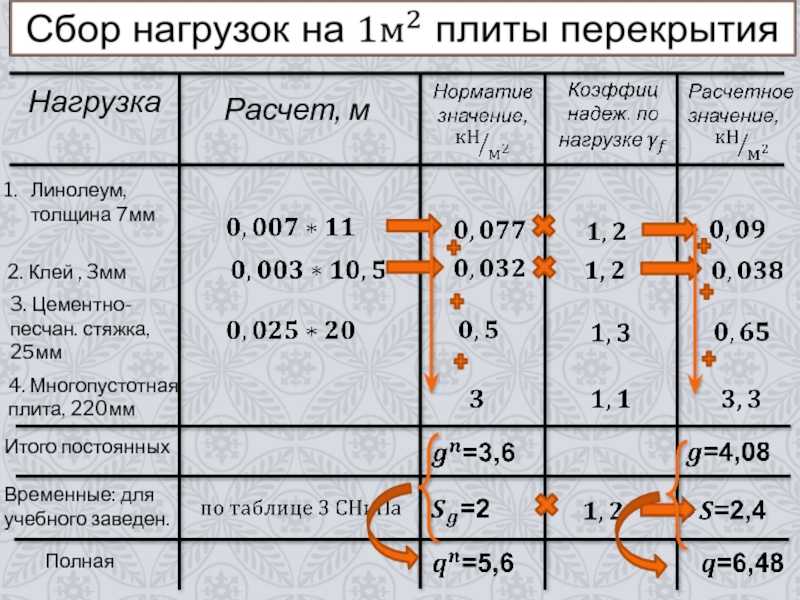 5 = Mа√2 = 1219.94.1.4142 = 1725.25 кгс.м. Так как в процессе расчета, который предполагает данный пример, необходимо какое-то одно значение момента, можно взять во внимание среднее расчетное значение между моментом для бетона и арматуры: М = (Ма + Мб)/2 = 1.207Ма = 1472.6 кгс.м. Следует брать во внимание, что при отрицании такого предположения можно рассчитать арматуру по моменту, который действует на бетон.
5 = Mа√2 = 1219.94.1.4142 = 1725.25 кгс.м. Так как в процессе расчета, который предполагает данный пример, необходимо какое-то одно значение момента, можно взять во внимание среднее расчетное значение между моментом для бетона и арматуры: М = (Ма + Мб)/2 = 1.207Ма = 1472.6 кгс.м. Следует брать во внимание, что при отрицании такого предположения можно рассчитать арматуру по моменту, который действует на бетон.
Вернуться к оглавлению
Сечение арматуры
Схема перекрытия по профлисту.
Данный пример расчета монолитной плиты предполагает определение сечения арматуры в продольном и в поперечном направлениях. В момент использования какой бы то ни было методики следует помнить о высоте расположения арматуры, которая может быть разной. Так, для арматуры, которая располагается параллельно оси х, предварительно можно принять h01 = 13 см, а вот арматура, располагаемая параллельно оси z, предполагает принятие h02 = 11 см. Такой вариант верен, так как диаметр арматуры пока неизвестен. Расчет по старой методике проиллюстрирован в ИЗОБРАЖЕНИИ 2. А вот используя вспомогательную таблицу, которую вы увидите на ИЗОБРАЖЕНИИ 3, можно найти в процессе расчета: η1 = 0.961 и ξ1 = 0.077. η2 = 0.945 и ξ2 = 0.11.
Такой вариант верен, так как диаметр арматуры пока неизвестен. Расчет по старой методике проиллюстрирован в ИЗОБРАЖЕНИИ 2. А вот используя вспомогательную таблицу, которую вы увидите на ИЗОБРАЖЕНИИ 3, можно найти в процессе расчета: η1 = 0.961 и ξ1 = 0.077. η2 = 0.945 и ξ2 = 0.11.
Схема примера несъемной опалубки.
В таблице указаны данные, необходимые в ходе расчета изгибаемого элемента прямоугольного сечения. Элементы при этом армированы одиночной арматурой. А как производится расчет требуемой площади сечения арматуры, можно увидеть на ИЗОБРАЖЕНИИ 4. Если для унификации принять продольную, а также поперечную арматуру, диаметр которой будет равен 10 мм, пересчитав показатель сечения поперечной арматуры, приняв во внимание h02 = 12 см, мы получим то, что вы сможете увидеть, взглянув на ИЗОБРАЖЕНИЕ 5. Таким образом, для армирования одного погонного метра можно применить 5 стержней поперечной арматуры и столько же продольной.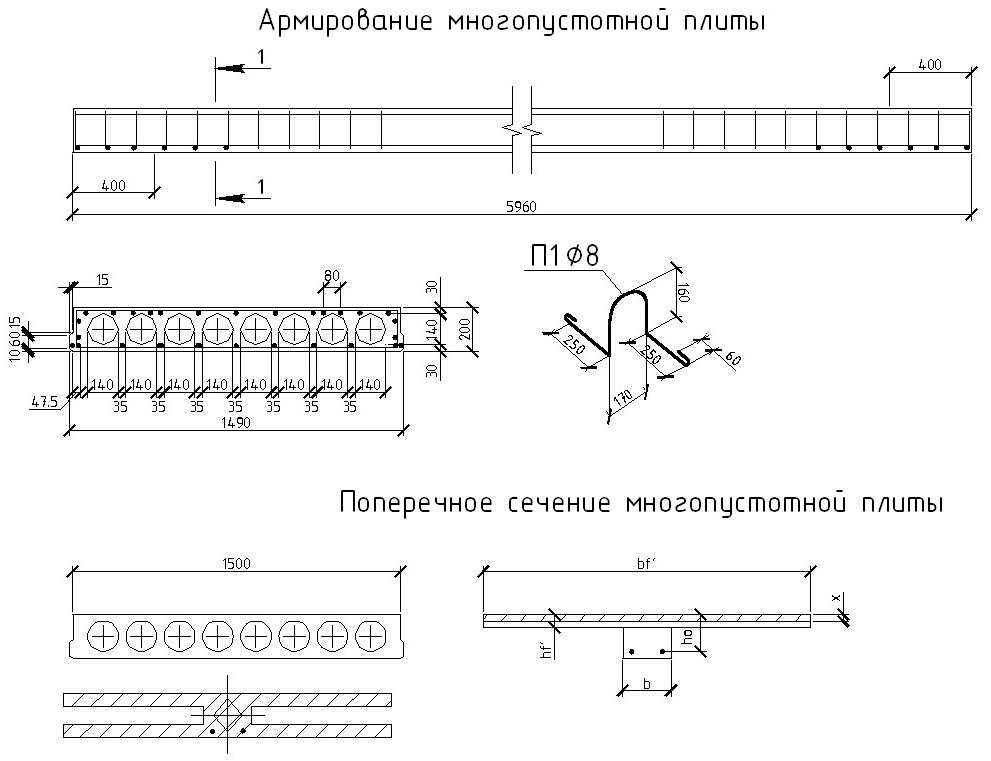 В конечном итоге получится сетка, которая имеет ячейки 200х200 мм. Арматура для одного погонного метра будет иметь площадь сечения, равную 3.93х2 = 7.86 см2. Это один пример подбора сечения арматуры, а вот расчет удобно будет производить, используя ИЗОБРАЖЕНИЕ 6.
В конечном итоге получится сетка, которая имеет ячейки 200х200 мм. Арматура для одного погонного метра будет иметь площадь сечения, равную 3.93х2 = 7.86 см2. Это один пример подбора сечения арматуры, а вот расчет удобно будет производить, используя ИЗОБРАЖЕНИЕ 6.
Все изделие предполагает использование 50 стержней, длина которых может варьироваться в пределах от 5.2 до 5.4 метра. Учитывая то, что в верхней части сечение арматуры имеет хороший запас, можно уменьшить число стержней до 4, которые расположены в нижнем слое, площадь сечения арматуры в этом случае окажется равна 3.14 см2 либо 15.7 см2 по длине плиты.
Вернуться к оглавлению
Основные параметры
Схема расчета бетона на фундамент.
Вышеприведенный расчет был простым, но, чтобы уменьшить количество арматуры, его следует усложнить, т. к максимальный изгибающий момент будет действовать лишь в центральной части плиты. Момент в местах приближения к опорам-стенам стремится к нулю, следовательно, остальные метры, исключая центральные, можно армировать, используя арматуру, которая имеет меньший диаметр. А вот размер ячеек для арматуры, которая имеет диаметр, равный 10 мм, увеличивать не следует, так как распределенная нагрузка на плиту перекрытия считается условной.
А вот размер ячеек для арматуры, которая имеет диаметр, равный 10 мм, увеличивать не следует, так как распределенная нагрузка на плиту перекрытия считается условной.
Следует помнить, что существующие способы расчета монолитной плиты перекрытия, которая опирается по контуру, в условиях панельных построек предполагают применение дополнительного коэффициента, который будет учитывать пространственную работу изделия, ведь воздействие нагрузки заставит плиту прогибаться, что предполагает концентрированное применение арматуры в центральной части плиты. Использование подобного коэффициента позволяет максимум на 10 процентов уменьшить сечение арматуры. Но для железобетонных плит, которые изготавливаются не в стенах завода, а в условиях стройплощадки, применение дополнительного коэффициента не обязательно. Прежде всего это обусловлено необходимостью дополнительных расчетов на раскрытие возможных трещин, на прогиб, на уровень минимального армирования. Более того, чем большее количество арматуры имеет плита, тем меньше окажется прогиб в центре и тем проще его можно устранить либо замаскировать в процессе финишной отделки.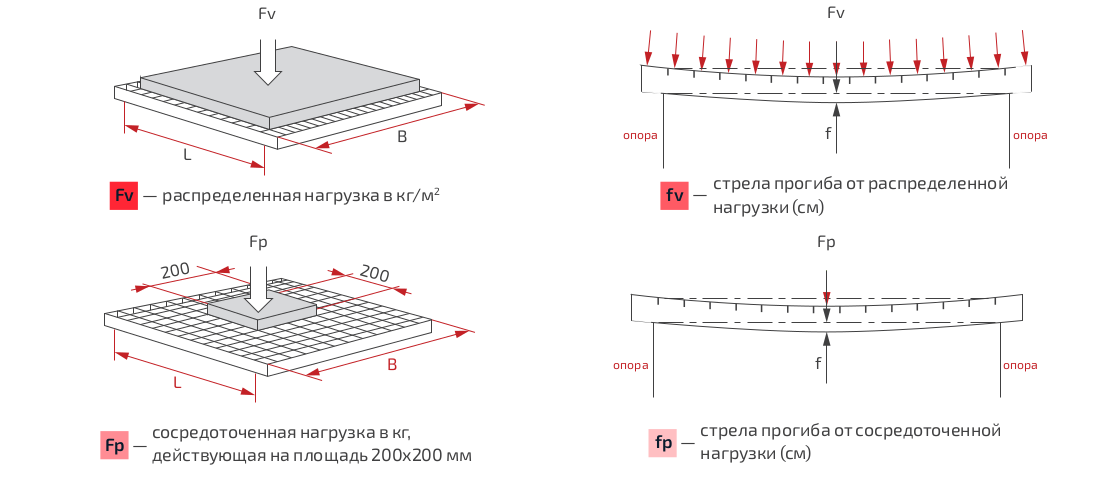
Так, если использовать рекомендации, которые предполагают расчет сборной сплошной плиты перекрытия общественных и жилых зданий, тогда площадь сечения арматуры, которая принадлежит к нижнему слою, по длине плиты окажется равна примерно А01 = 9.5 см2 , что примерно в 1.6 раза меньше полученного в данном расчете результата, но в этом случае необходимо помнить, что максимальная концентрация арматуры должна оказаться посредине пролета, поэтому разделить полученную цифру на 5 м длины не допустимо. Однако это значение площади сечения позволяет приблизительно оценить, какое количество арматуры можно сэкономить после проведения расчетов.
Вернуться к оглавлению
Расчет прямоугольной плиты
Схема монолитного перекрытия своими руками.
Данный пример для упрощения расчетов предполагает использование всех параметров, кроме ширины и длины помещения, таких же как в первом примере. Бесспорно, моменты, которые действуют относительно оси х и z в прямоугольных плитах перекрытия, не равны. И чем больше окажется разница между шириной и длиной помещения, тем больше плита перекрытия станет напоминать балку, размещенную на шарнирных опорах, а в момент достижения определенного значения уровень влияния поперечной арматуры будет почти неизменным.
И чем больше окажется разница между шириной и длиной помещения, тем больше плита перекрытия станет напоминать балку, размещенную на шарнирных опорах, а в момент достижения определенного значения уровень влияния поперечной арматуры будет почти неизменным.
Существующие экспериментальные данные и опыт, полученный при проектировании, показывают, что при соотношении λ = l2 / l1 > 3 показатель поперечного момента окажется в 5 раз меньше продольного. А в случае когда λ ≤ 3, определить соотношение моментов допустимо, используя эмпирический график, который проиллюстрирован на ИЗОБРАЖЕНИИ 7, где можно проследить зависимость моментов от λ. Под единицей подразумеваются плиты монолитного типа с контурным шарнирным опиранием, двойка предполагает плиты с трехсторонним шарнирным опиранием. График изображает пунктир, который показывает допустимые нижние пределы в процессе подбора арматуры, а в скобках указаны значения λ, что применимо для плит с трехсторонним опиранием. При этом λ < 0,5 m = λ, нижние пределы m = λ/2. Но в этом случае интерес представляет лишь кривая №1, которая отображает теоретические значения. На ней можно видеть подтверждение предположения, что уровень соотношения моментов равен 1 для плиты квадратной формы, по ней можно определить уровень моментов для остальных соотношений ширины и длины.
Но в этом случае интерес представляет лишь кривая №1, которая отображает теоретические значения. На ней можно видеть подтверждение предположения, что уровень соотношения моментов равен 1 для плиты квадратной формы, по ней можно определить уровень моментов для остальных соотношений ширины и длины.
Вернуться к оглавлению
Формулы и коэффициенты
Схема монтажа перекрытия.
Так, для расчета плиты перекрытия монолитного типа используется помещение, которое имеет длину, равную 8 м, и ширину, равную 5 м. Следовательно, расчетные пролеты окажутся равны l2 = 8 м и l1 = 5 м. При этом λ = 8/5 = 1.6, уровень соотношения моментов равен m2/m1 = 0.49, а вот m2 = 0.49m1. По причине, что общий момент равняется M = m1 + m2, то M = m1 +0.49m1 или m1 = M/1.49, общий момент следует определять по короткой стороне, что обусловлено разумностью решения: Ма = ql12/8 = 775 х 52 / 8 = 2421. 875 кгс.м. Дальнейший расчет приведен на ИЗОБРАЖЕНИИ 8.
875 кгс.м. Дальнейший расчет приведен на ИЗОБРАЖЕНИИ 8.
Так, для армирования одного погонного метра плиты перекрытия следует применить 5 стержней арматуры, диаметр арматуры в этом случае будет равен 10 мм, при этом длина может варьироваться до 5.4 м, а начальный предел может быть равен 5.2 м. Показатель площади сечения продольной арматуры для одного погонного метра равняется 3.93 см2. Поперечное армирование допускает использование 4 стержней. Диаметр арматуры плиты при этом равен 8 мм, максимальная длина равна 8.4 м, при начальном значении в 8.2 м. Сечение поперечной арматуры имеет площадь, равную 2.01 см2, что необходимо для одного погонного метра.
Стоит помнить, что приведенный расчет плиты перекрытия можно считать упрощенным вариантом. При желании, уменьшив сечение используемой арматуры и изменив класс бетона либо и вовсе высоту плиты, можно уменьшить нагрузку, рассмотрев разные варианты загрузки плиты. Вычисления позволят понять, даст ли это какой-то эффект.
Схема строительства дома.
Так, для простоты расчета плиты перекрытия в примере не было учтено влияние площадок, выступающих в качестве опор, а вот если на данные участки сверху станут опираться стены, приближая таким образом плиту к защемлению, тогда при более значительной массе стен данная нагрузка должна быть учтена, это применимо в случае, когда ширина данных опорных участков окажется больше 1/2 ширины стены. В случае когда показатель ширины опорных участков окажется меньше или будет равен 1/2 ширине стены, тогда будет необходим дополнительный расчет стены на прочность. Но даже в этом случае вероятность, что на опорные участки не станет передаваться нагрузка от массы стены, окажется велика.
Вернуться к оглавлению
Пример варианта при конкретной ширине плиты
Возьмем за основу ширину опорных областей плиты, равную 370 мм, что применимо для кирпичных стен, имеющих ширину в 510 мм. Этот вариант расчета предполагает высокую вероятность передачи на опорную область плиты нагрузки от стены. Так, если плита будет удерживать стены, ширина которых равна 510 мм, а высота — 2.8 м, а на стены станет опираться плита следующего этажа, сосредоточенная постоянная нагрузка окажется равна.
Так, если плита будет удерживать стены, ширина которых равна 510 мм, а высота — 2.8 м, а на стены станет опираться плита следующего этажа, сосредоточенная постоянная нагрузка окажется равна.
Более правильным в этом случае было бы брать во внимание в процессе расчета плиту перекрытия в качестве шарнирно опертого ригеля с консолями, а уровень сосредоточенной нагрузки — в качестве неравномерно распределенной нагрузки на консоли. Кроме того, чем ближе к краю, тем нагрузка была бы больше, но для упрощения можно предположить, что данная нагрузка равномерно распределяется на консолях, составляя 3199.6/0.37 = 8647, 56 кг/м. Уровень момента на шарнирных опорах от подобной нагрузки будет равен 591.926 кгс.м.
Это значит, что:
- в пролете m1 максимальный момент будет уменьшен и окажется равен m1 = 1717.74 — 591.926 = 1126 кгс.м. Сечение арматуры плиты перекрытия допустимо уменьшить либо и вовсе изменить остальные параметры плиты;
- изгибающий опорный момент вызовет в верхней части плиты растягивающие напряжения, бетон на это в области растяжения не рассчитан, значит, необходимо дополнительно армировать в верхней части плиты перекрытия монолитного типа или уменьшить значение ширины опорного участка, что позволит уменьшить нагрузку на опорные участки.
 На случай если верхняя часть изделия не будет дополнительно армирована, плита перекрытия станет образовывать трещины, превратившись в плиту шарнирно-опертого типа без консолей.
На случай если верхняя часть изделия не будет дополнительно армирована, плита перекрытия станет образовывать трещины, превратившись в плиту шарнирно-опертого типа без консолей.
Данный вариант расчета загружения следует рассматривать вместе с вариантом, который предполагает, что плита перекрытия уже имеется, а стены — нет, что исключает временную нагрузку на плиту.
Расчет перекрытия — Портал гражданского строительства
ВВЕДЕНИЕ
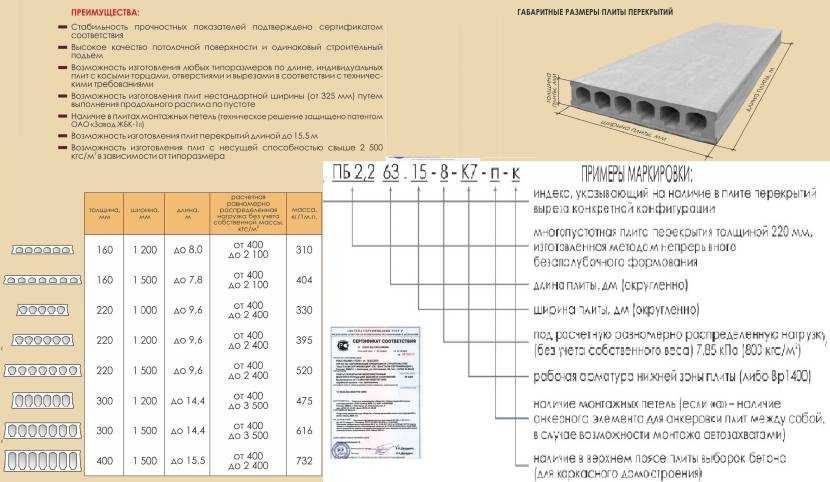
Перекрытие — это конструктивный элемент, который используется для поддержки потолков и полов. Он сделан из бетона, и для его поддержки предусмотрена арматура. Его толщина составляет несколько дюймов, и он опирается на балки и колонны. Подсчитано, что бетонная плита служит от 30 до 100 лет, если она построена из бетона и стали хорошего качества. Обычно для жилых целей используется М20.
Обычно для жилых целей используется М20.
Существует два типа плит – односторонняя плита и двусторонняя плита. Двухсторонние плиты поддерживаются с четырех сторон, а односторонние плиты поддерживаются с двух противоположных сторон. Двухсторонние плиты несут нагрузку в двух направлениях, поэтому армирование предусмотрено в обоих направлениях. Принимая во внимание, что в односторонней плите арматура предоставляется в одном направлении, поскольку она несет нагрузку в одном направлении. В односторонней плите отношение более длинного пролета к меньшему больше или равно 2, в то время как в двусторонней плите отношение более длинного пролета к меньшему меньше 2.
Здесь в этой задаче сначала показан план дома, затем панели перекрытия изображены в соответствии с планом дома. План, используемый для гравитационного анализа здания, также аналогичен панелям перекрытий. Здесь берутся первичные балки, а второстепенные балки не учитываются, чтобы сократить расчеты. Кроме того, отношение более длинного пролета к более короткому во всех панельных плитах составляет менее 2, поэтому все панели перекрытий являются двусторонними плитами. Метод проектирования соответствует Приложению D стандарта IS 456:2000.
Метод проектирования соответствует Приложению D стандарта IS 456:2000.
КОНСТРУКЦИЯ ПЛИТЫ:
Конструкция типовой плиты перекрытия:
У нас толщина плиты 130 мм.
С учетом бетона марки М20 и стали Fe 500 диаметром 10 мм
Эффективная глубина: (130-15-10/2) = 110 мм.
Расчет нагрузки:
Фактическая нагрузка = 2 кН/м 2
Собственный вес плиты = 3,25 кН/м 2
Отделка пола = 1 кН/м 2 Всего = 6 кН/м 9 9 м 2
Определение моментов плит (плита с боковым защемлением):
Согласно стандарту IS 456:2000, пункт D-1.1, максимальный изгибающий момент на единицу ширины плиты определяется формулой: x 2
M Y = α Y WL Y 2
, где L x и L Y — это длина седл. , α y – моментные коэффициенты,
M x и M y представляют собой моменты на полосах единичной ширины, пролетающих l x и l y соответственно,
Вт = общая расчетная нагрузка на единицу площади.
Проверка толщины
Здесь максимальный момент взят из таблицы ниже.
Отсюда Safe
Расчет B.M. Коэффициент
| № панели | л x (м) | л у (м) | л у /л x | Тип | Негатив α x | Отрицательный α y | Положительный α x | Положительный α y | |
| 1 | 3,35 | 4,42 | 1,32 | Две смежные кромки прерывистые | 0,066 | 0,047 | 0,050 | 0,035 | |
| 2 | 3,35 | 3,73 | 1.11 | Одна длинная кромка прерывистая | 0,045 | 0,037 | 0,034 | 0,028 | |
| 3 | 3,35 | 3,73 | 1. 11 11 | Одна длинная кромка прерывистая | 0,045 | 0,037 | 0,034 | 0,028 | |
| 4 | 3,35 | 4,42 | 1,32 | Две смежные кромки прерывистые | 0,066 | 0,047 | 0,050 | 0,035 | |
| 5 | 3,65 | 4,42 | 1,21 | Одна короткая кромка прерывистая | 0,048 | 0,037 | 0,036 | 0,028 | |
| 6 | 3,65 | 3,73 | 1,02 | Внутренняя панель | 0,033 | 0,032 | 0,025 | 0,024 | |
| 7 | 2,72 | 3,65 | 1,34 | Внутренняя панель | 0,049 | 0,032 | 0,037 | 0,024 | |
| 8 | 3,65 | 3,73 | 1,02 | Внутренняя панель | 0,033 | 0,032 | 0,025 | 0,024 | |
| 9 | 3,65 | 4,42 | 1,21 | Одна короткая кромка прерывистая | 0,048 | 0,037 | 0,036 | 0,028 | |
| 10 | 3,6 | 4,42 | 1,23 | Одна короткая кромка прерывистая | 0,049 | 0,037 | 0,037 | 0,028 | |
| 11 | 3,6 | 3,73 | 1,04 | Внутренняя панель | 0,034 | 0,032 | 0,025 | 0,024 | |
| 12 | 2,72 | 3,6 | 1,32 | Внутренняя панель | 0,048 | 0,032 | 0,037 | 0,024 | |
| 13 | 3,6 | 3,73 | 1,04 | Внутренняя панель | 0,034 | 0,032 | 0,025 | 0,024 | |
| 14 | 3,6 | 4,42 | 1,23 | Одна короткая кромка прерывистая | 0,049 | 0,037 | 0,037 | 0,028 | |
| 15 | 3,6 | 4,42 | 1,23 | Одна короткая кромка прерывистая | 0,049 | 0,037 | 0,037 | 0,028 | |
| 16 | 3,6 | 3,73 | 1,04 | Внутренняя панель | 0,034 | 0,032 | 0,025 | 0,024 | |
| 17 | 2,72 | 3,6 | 1,32 | Внутренняя панель | 0,048 | 0,032 | 0,037 | 0,024 | |
| 18 | 3,6 | 3,73 | 1,04 | Внутренняя панель | 0,034 | 0,032 | 0,025 | 0,024 | |
| 19 | 3,6 | 4,42 | 1,23 | Одна короткая кромка прерывистая | 0,049 | 0,037 | 0,037 | 0,028 | |
| 20 | 3,65 | 4,42 | 1,21 | Одна короткая кромка прерывистая | 0,048 | 0,037 | 0,036 | 0,028 | |
| 21 | 3,65 | 3,73 | 1,02 | Внутренняя панель | 0,033 | 0,032 | 0,025 | 0,024 | |
| 22 | 2,72 | 3,65 | 1,34 | Внутренняя панель | 0,049 | 0,032 | 0,037 | 0,024 | |
| 23 | 3,65 | 3,73 | 1,02 | Внутренняя панель | 0,033 | 0,032 | 0,025 | 0,024 | |
| 24 | 3,65 | 4,42 | 1,21 | Одна короткая кромка прерывистая | 0,048 | 0,037 | 0,036 | 0,028 | |
| 25 | 3,35 | 4,42 | 1,32 | Две смежные кромки прерывистые | 0,066 | 0,047 | 0,050 | 0,035 | |
| 26 | 3,35 | 3,73 | 1.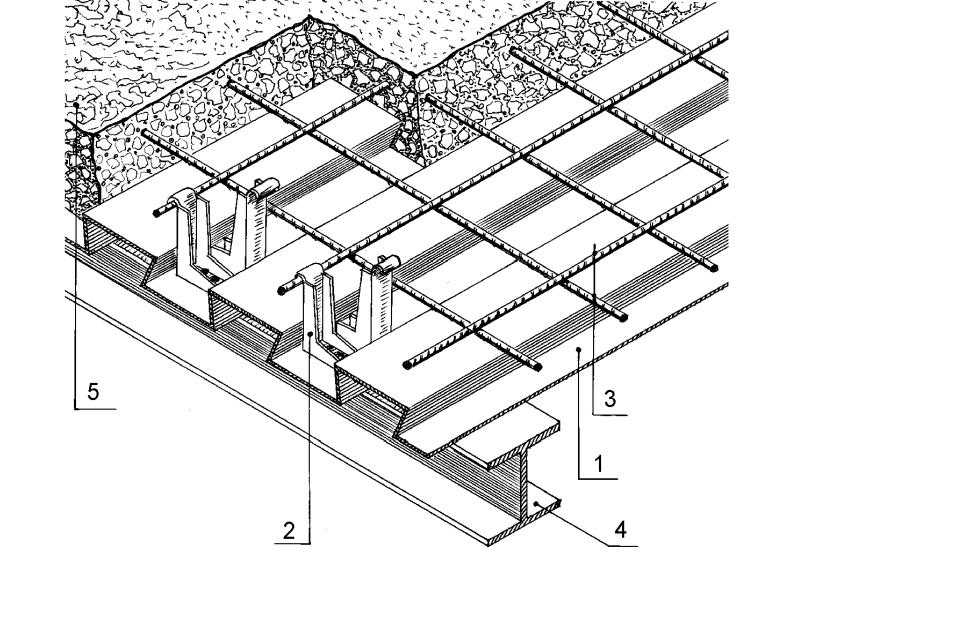 11 11 | Одна длинная кромка прерывистая | 0,045 | 0,037 | 0,034 | 0,028 | |
| 27 | 3,35 | 3,73 | 1.11 | Одна длинная кромка прерывистая | 0,045 | 0,037 | 0,034 | 0,028 | |
| 28 | 3,35 | 4,42 | 1,32 | Две смежные кромки прерывистые | 0,066 | 0,047 | 0,050 | 0,035 |
Расчет моментов
| Панель № | Коэффициент B.M для более короткого направления M x =α x wl x 2 x 1,5 | Коэффициент B.M для более длинного направления M y =α y wl y 2 x 1,5 | ||
| Рядом с опорой (-ve) | Рядом с опорой (+ve) | Рядом с опорой (-ve) | Рядом с опорой (+ve) | |
| 1 | 6,94 | 5,26 | 8,61 | 6,41 |
| 2 | 4,73 | 3,58 | 4,83 | 3,65 |
| 3 | 4,73 | 3,58 | 4,83 | 3,65 |
| 4 | 6,94 | 5,26 | 8,61 | 6,41 |
| 5 | 6,00 | 4,50 | 6,78 | 5. 13 13 |
| 6 | 4.12 | 3,12 | 4,17 | 3,13 |
| 7 | 3,40 | 2,57 | 4,00 | 3,00 |
| 8 | 4.12 | 3,12 | 4,17 | 3,13 |
| 9 | 6,00 | 4,50 | 6,78 | 5.13 |
| 10 | 5,95 | 4,50 | 6,78 | 5.13 |
| 11 | 4.13 | 3,04 | 4,17 | 3,13 |
| 12 | 3,33 | 2,57 | 3,89 | 2,92 |
| 13 | 4.13 | 3,04 | 4,17 | 3,13 |
| 14 | 5,95 | 4,50 | 6,78 | 5.13 |
| 15 | 5,95 | 4,50 | 6,78 | 5.13 |
| 16 | 4.13 | 3,04 | 4,17 | 3,13 |
| 17 | 3,33 | 2,57 | 3,89 | 2,92 |
| 18 | 4. 13 13 | 3,04 | 4.17 | 3,13 |
| 19 | 5,95 | 4,50 | 6,78 | 5.13 |
| 20 | 6,00 | 4,50 | 6,78 | 5.13 |
| 21 | 4.12 | 3,12 | 4,17 | 3,13 |
| 22 | 3,40 | 2,57 | 4,00 | 3,00 |
| 23 | 4,12 | 3,12 | 4,17 | 3,13 |
| 24 | 6,00 | 4,50 | 6,78 | 5.13 |
| 25 | 6,94 | 5,26 | 8,61 | 6,41 |
| 26 | 4,73 | 3,58 | 4,83 | 3,65 |
| 27 | 4,73 | 3,58 | 4,83 | 3,65 |
| 28 | 6,94 | 5,26 | 8,61 | 6,41 |
Расчет площади стали
| Пролет | Положение моментов | Моменты (кНм) | М и /шп 2 | Платина % | Ast в мм 2 (обязательно) | Ast в мм 2 (прилагается) | Расстояние между стержнями 10 мм @ c/c |
| Короткий | Рядом с опорой | 6,94 | 0,57 | 0,162 | 178,20 | 250 | 300 |
| Средний пролет | 5,26 | 0,43 | 0,121 | 133. 10 10 | 250 | 300 | |
| Длинный | Рядом с опорой | 8,61 | 0,71 | 0,204 | 224,40 | 250 | 300 |
| Средний пролет | 6,41 | 0,53 | 0,150 | 165,00 | 250 | 300 | |
| Короткий | Рядом с опорой | 4,73 | 0,39 | 0,110 | 121.00 | 250 | 300 |
| Средний пролет | 3,58 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Возле поддержки | 4,83 | 0,40 | 0,113 | 124,30 | 250 | 300 |
| Средний пролет | 3,65 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 4,73 | 0,39 | 0,110 | 121. 00 00 | 250 | 300 |
| Средний пролет | 3,58 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,83 | 0,40 | 0,113 | 124,30 | 250 | 300 |
| Средний пролет | 3,65 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 6,94 | 0,57 | 0,162 | 178,20 | 250 | 300 |
| Средний пролет | 5,26 | 0,43 | 0,121 | 133.10 | 250 | 300 | |
| Длинный | Рядом с опорой | 8,61 | 0,71 | 0,204 | 224,40 | 250 | 300 |
| Средний пролет | 6,41 | 0,53 | 0,150 | 165,00 | 250 | 300 | |
| Короткий | Рядом с опорой | 6,00 | 0,50 | 0,142 | 156,20 | 250 | 300 |
| Средний пролет | 4,50 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5.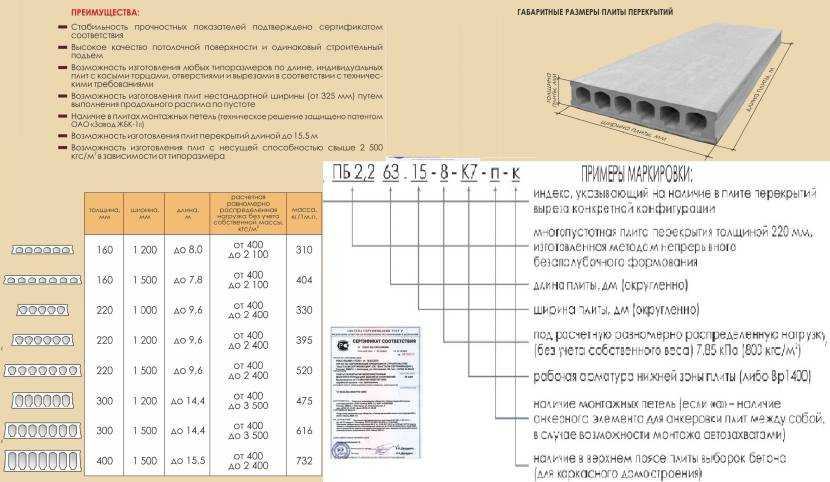 13 13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.12 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,12 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 3,40 | 0,28 | 0,084 | 92,40 | 250 | 300 |
| Средний пролет | 2,57 | 0,21 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,00 | 0,33 | 0,093 | 102. 30 30 | 250 | 300 |
| Средний пролет | 3,00 | 0,25 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.12 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,12 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 6,00 | 0,50 | 0,142 | 156,20 | 250 | 300 |
| Средний пролет | 4,50 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,145 | 159,50 | 250 | 300 |
| Средний пролет | 5.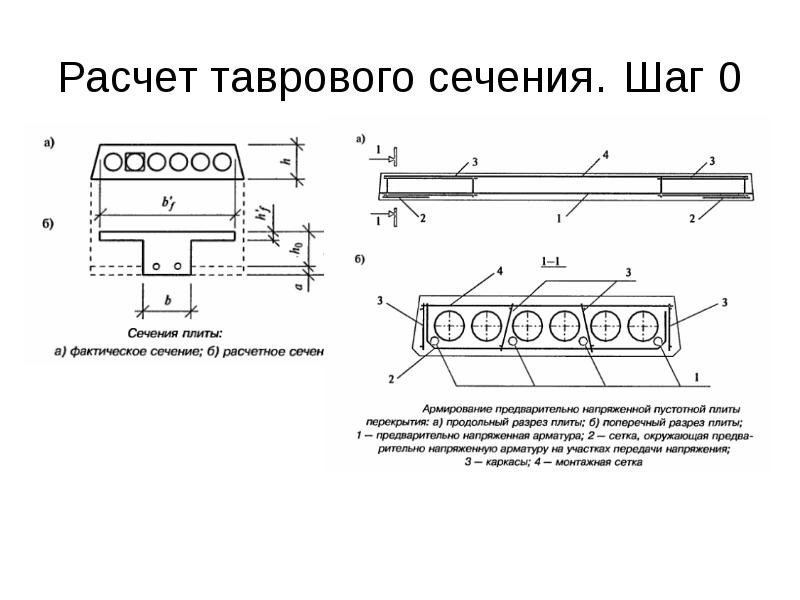 13 13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 5,95 | 0,49 | 0,139 | 152,90 | 250 | 300 |
| Средний пролет | 4,50 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5.13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.13 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,04 | 0,25 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3. 13 13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 3,33 | 0,28 | 0,084 | 92,40 | 250 | 300 |
| Средний пролет | 2,57 | 0,21 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 3,89 | 0,32 | 0,090 | 99.00 | 250 | 300 |
| Средний пролет | 2,92 | 0,24 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.13 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,04 | 0,25 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 5,95 | 0,49 | 0,139 | 152,90 | 250 | 300 |
| Средний пролет | 4,5 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5. 13 13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 5,95 | 0,49 | 0,139 | 152,90 | 250 | 300 |
| Средний пролет | 4,5 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5.13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.13 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,04 | 0,25 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 3,33 | 0,28 | 0,084 | 92,40 | 250 | 300 |
| Средний пролет | 2,57 | 0,21 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 3,89 | 0,32 | 0,090 | 99. 00 00 | 250 | 300 |
| Средний пролет | 2,92 | 0,24 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.13 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,04 | 0,25 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 5,95 | 0,49 | 0,139 | 152,90 | 250 | 300 |
| Средний пролет | 4,5 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5. 13 13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 6 | 0,50 | 0,142 | 156,20 | 250 | 300 |
| Средний пролет | 4,5 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5.13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.12 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,12 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 3,4 | 0,28 | 0,084 | 92,40 | 250 | 300 |
| Средний пролет | 2,57 | 0,21 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4 | 0,33 | 0,093 | 102. 30 30 | 250 | 300 |
| Средний пролет | 3 | 0,25 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 4.12 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,12 | 0,26 | 0,084 | 92.40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,17 | 0,34 | 0,096 | 105,60 | 250 | 300 |
| Средний пролет | 3,13 | 0,26 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 6 | 0,50 | 0,142 | 156,20 | 250 | 300 |
| Средний пролет | 4,5 | 0,37 | 0,105 | 115,50 | 250 | 300 | |
| Длинный | Рядом с опорой | 6,78 | 0,56 | 0,159 | 174,90 | 250 | 300 |
| Средний пролет | 5.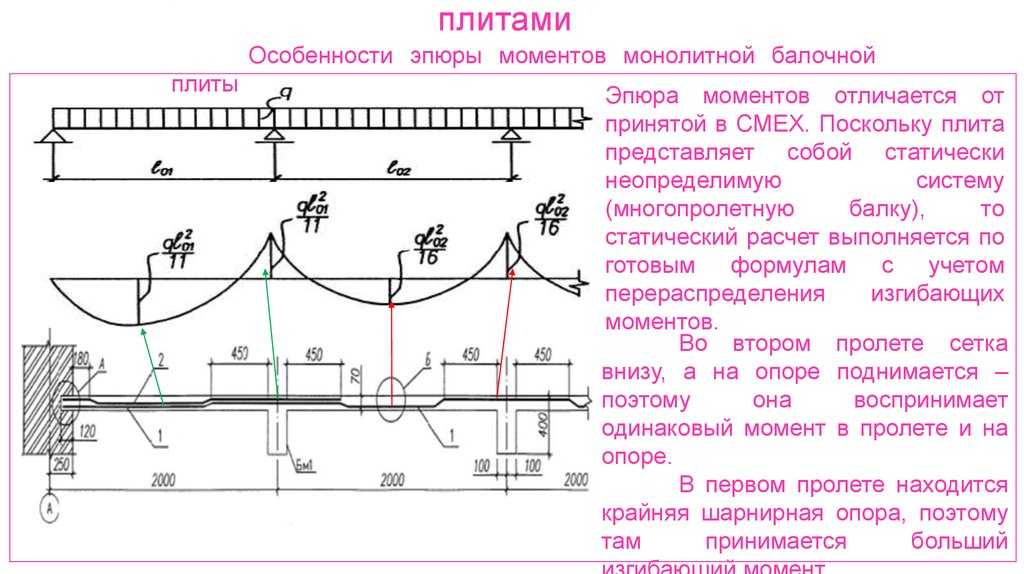 13 13 | 0,42 | 0,119 | 130,90 | 250 | 300 | |
| Короткий | Рядом с опорой | 6,94 | 0,57 | 0,162 | 178,20 | 250 | 300 |
| Средний пролет | 5,26 | 0,43 | 0,121 | 133.10 | 250 | 300 | |
| Длинный | Рядом с опорой | 8,61 | 0,71 | 0,204 | 224,40 | 250 | 300 |
| Средний пролет | 6,41 | 0,53 | 0,150 | 165,00 | 250 | 300 | |
| Короткий | Рядом с опорой | 4,73 | 0,39 | 0,110 | 121.00 | 250 | 300 |
| Средний пролет | 3,58 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,83 | 0,40 | 0,113 | 124,30 | 250 | 300 |
| Средний пролет | 3,65 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 4,73 | 0,39 | 0,110 | 121. 00 00 | 250 | 300 |
| Средний пролет | 3,58 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Длинный | Рядом с опорой | 4,83 | 0,40 | 0,113 | 124,30 | 250 | 300 |
| Средний пролет | 3,65 | 0,30 | 0,084 | 92,40 | 250 | 300 | |
| Короткий | Рядом с опорой | 6,94 | 0,57 | 0,162 | 178,20 | 250 | 300 |
| Средний пролет | 5,26 | 0,43 | 0,121 | 133.10 | 250 | 300 | |
| Длинный | Рядом с опорой | 8,61 | 0,71 | 0,204 | 224,40 | 250 | 300 |
| Средний пролет | 6. 41 41 | 0,53 | 0,150 | 165,00 | 250 | 300 |
| Панель | Площадь стали для максимального момента в середине пролета (мм 2 ) | (3/4) Аст (мм 2 ) | 0,5 (3/4) Аст (мм 2 ) | Угол 1 | Угол 2 | Угол 3 | Угол 4 |
| 1 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 2 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 3 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 4 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 5 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 6 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 7 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 8 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 9 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 10 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 11 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 12 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 13 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 14 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 15 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 16 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 17 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 18 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 19 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 20 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 21 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 22 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 23 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 24 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 25 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 26 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 27 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
| 28 | 224,4 | 168,3 | 84,15 | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм | 8Φ@300 мм |
ДЕТАЛИ УСИЛЕНИЯ ПЛИТЫ
ПОЛОЖЕНИЕ УСИЛЕНИЯ КРУТИ
Поделиться этим постом
Если у вас есть вопросы, вы можете задать вопрос здесь .
Расчет прогиба железобетонных плит
Новые функции
Бетонные конструкции широко используются в строительстве. В таких конструкциях плиты являются ключевыми конструктивными элементами, противостоящими силе тяжести и временным нагрузкам каждого этажа. Проектирование бетонных плит представляет собой повторяющийся процесс. В основном необходимо проверить два аспекта: i) сопротивление и ii) прогиб плит. Несмотря на то, что количество арматуры выбрано таким образом, чтобы противостоять нагрузкам на конструкцию, особое внимание следует уделить прогибам плит. Такая проверка прогибов может свидетельствовать о необходимости дополнительного армирования или о необходимости увеличения толщины плит.
Таким образом, был разработан расчет прогиба бетонных плит при трещинах. Явление растрескивания увеличивает общий прогиб плиты. Предельные состояния службы гарантируют, что отклонения плиты не превышают заданные предельные значения, чтобы избежать проблем с эксплуатационной надежностью.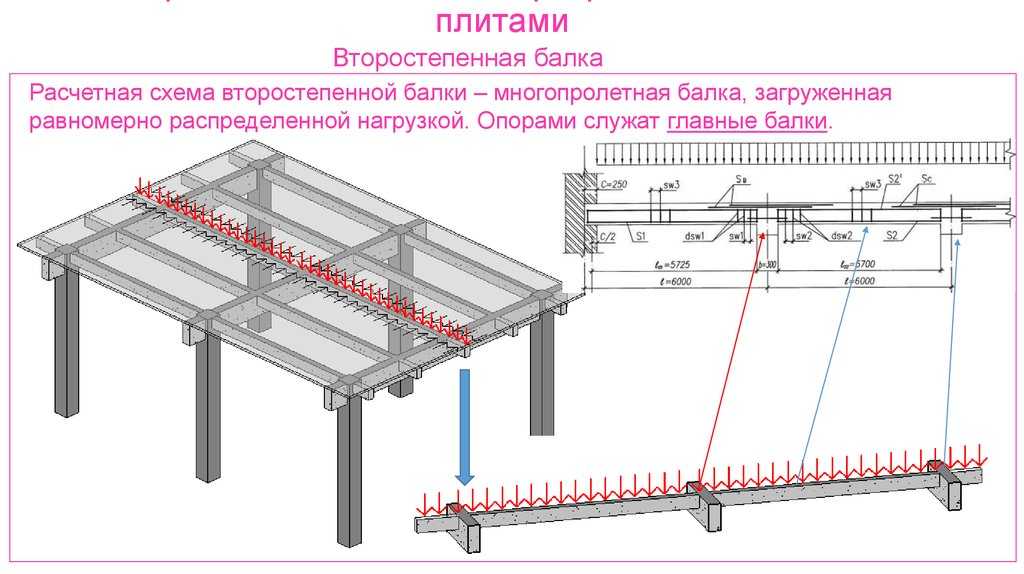
Что касается удобства эксплуатации, особое внимание следует уделить тому, чтобы ненесущие элементы не были повреждены прогибами здания. Этапы строительства анализируются, чтобы правильно оценить полные прогибы таких ненесущих элементов после их установки. В программном обеспечении SAFI GSE этапы строительства представлены сочетаниями нагрузок собственного веса, постоянного собственного веса и динамических нагрузок. Другие параметры, требуемые различными стандартами, могут быть отредактированы конечным пользователем.
Прогибы бетонных плит состоят из: немедленных прогибов и прогибов, зависящих от времени. Непосредственные прогибы рассчитываются для выбранных комбинаций нагрузок. Явления усадки и ползучести являются зависящими от времени эффектами, вызывающими отклонения в течение длительных периодов времени. Общие прогибы здания представляют собой комбинацию как немедленных, так и зависящих от времени прогибов.
Расчеты мгновенного прогиба трещины требуют итеративной процедуры анализа, при которой нагрузки применяются постепенно. Исходная жесткость конечного элемента рассчитывается с использованием изотропных упругих свойств бетона. С увеличением интенсивности нагружения увеличиваются и изгибные усилия в плитах. Таким образом, трещины могут образовываться вблизи областей с высоким изгибающим усилием. В этих местах инерция сечения плиты изменяется, и концепция эффективной инерции I e используется. Эффективная инерция рассчитывается по инерции без разрыва I g и инерции с полным разрывом I cr . Хорошо известное уравнение для расчета эффективной инерции I e представлено ниже: изменяются жесткости элементов, что требует формулировки конечных элементов ортотропной оболочки.
Исходная жесткость конечного элемента рассчитывается с использованием изотропных упругих свойств бетона. С увеличением интенсивности нагружения увеличиваются и изгибные усилия в плитах. Таким образом, трещины могут образовываться вблизи областей с высоким изгибающим усилием. В этих местах инерция сечения плиты изменяется, и концепция эффективной инерции I e используется. Эффективная инерция рассчитывается по инерции без разрыва I g и инерции с полным разрывом I cr . Хорошо известное уравнение для расчета эффективной инерции I e представлено ниже: изменяются жесткости элементов, что требует формулировки конечных элементов ортотропной оболочки.
Прогибы, зависящие от времени, рассчитываются с использованием непосредственных прогибов бетона с трещинами для указанных комбинаций нагрузок. В ГСЭ автоматизировано управление сочетаниями нагрузок для прогибов бетона с трещинами. CSA A23.3 предлагает следующее уравнение для расчета долговременных отклонений.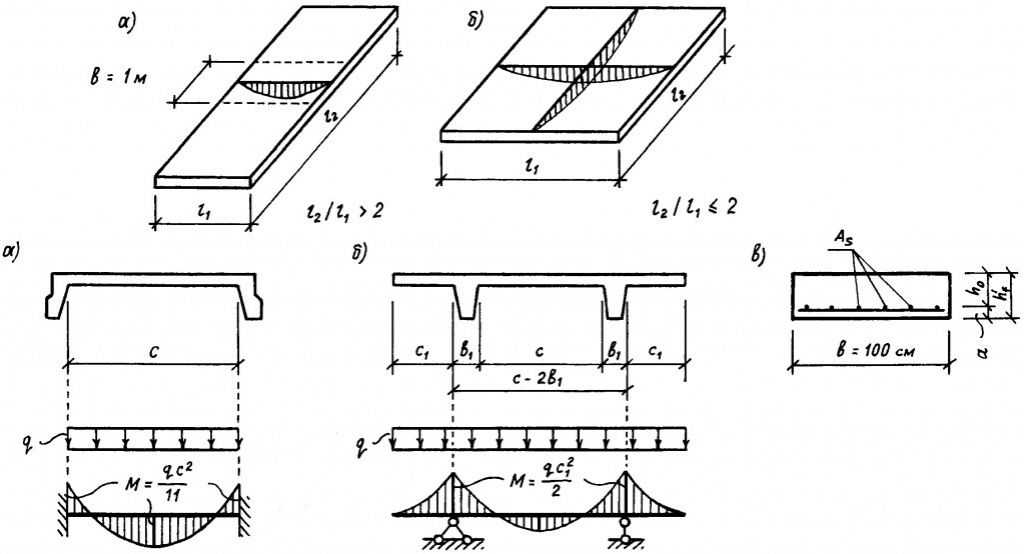
 На случай если верхняя часть изделия не будет дополнительно армирована, плита перекрытия станет образовывать трещины, превратившись в плиту шарнирно-опертого типа без консолей.
На случай если верхняя часть изделия не будет дополнительно армирована, плита перекрытия станет образовывать трещины, превратившись в плиту шарнирно-опертого типа без консолей.