Как высчитать угол 90 градусов рулеткой
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ.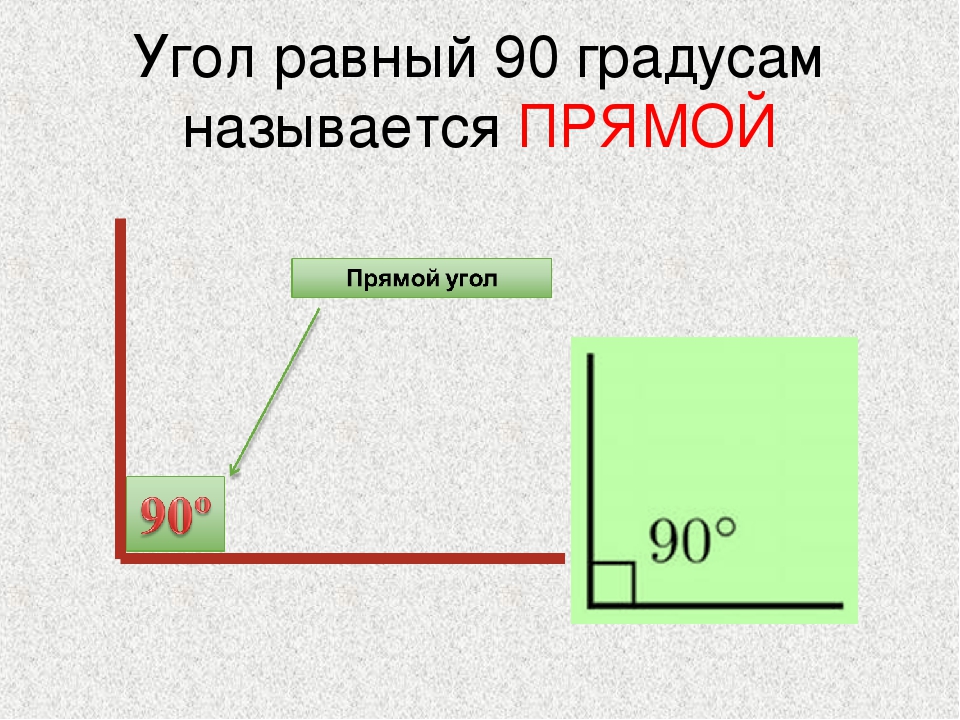 Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Теорема Пифагора
Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора.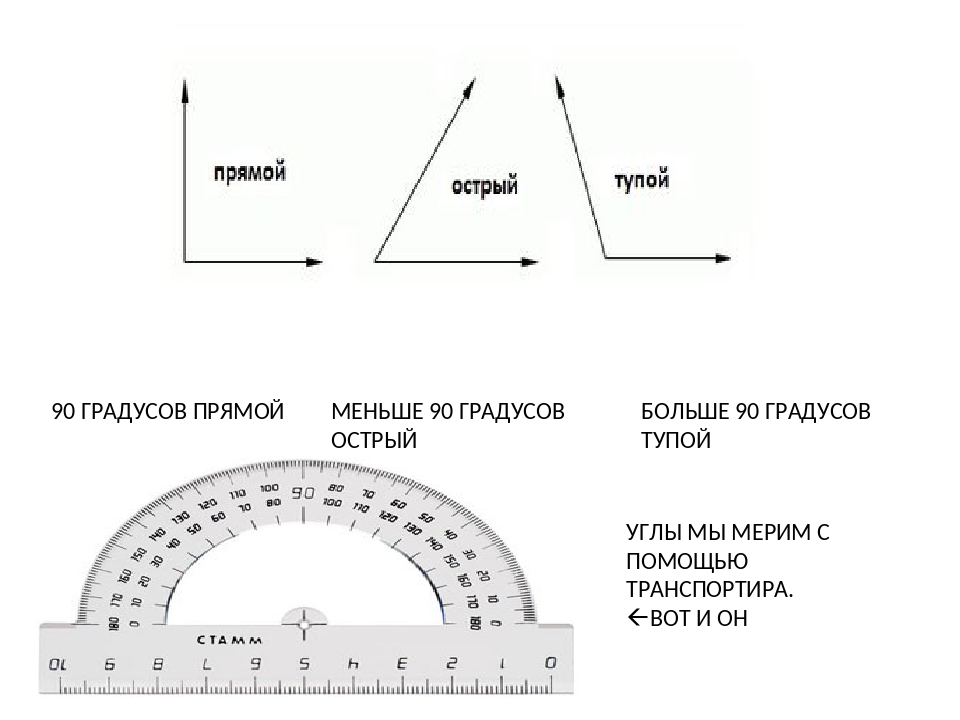 Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.
Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.
А теперь вернемся к нашим замерам и применим теорему на практике.
Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Египетский треугольник
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?
a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.
Как проверить угол с помощью египетского треугольника?
Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.
Как отмерить угол, используя рулетку
Можно самостоятельно смастерить угольник для замера углов:
- Соединяем две рейки одна перпендикулярно другой.
- Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
- Прибиваем третью рейку к одной отметке.
- Измеряем гипотенузу, прибиваем рейку ко второй метке.

- Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
- Обрезаем лишние концы.
Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.
Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.
Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.
У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.
Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.
Один и тот же размер при измерении разными рулетками может не совпадать.
Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.
Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.
Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:
- от предмета
Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.
При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.
Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.
Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.
Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.
Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.
На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.
Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.
Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.
При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.
Проделав два измерения нужно сложить результаты и получите точный размер.
На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.
Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.
В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.
Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.
Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.
Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.
А при использовании шурупа легко рисуются окружности нужного диаметра.
Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.
После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.
Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.
Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.
Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.
Писать конечно нужно карандашом, после чего все это легко стирается резинкой.
С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.
Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.
Ровно в месте перегиба и будет требуемый результат — 58см.
Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.
Вытягиваете ленту на 2м 11см и складываете ее пополам.
Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.
Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.
Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.
Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.
Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.
В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.
Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.
Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.
Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.
Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.
Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.
Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.
Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.
Как сделать прямой угол между стенами при штукатурке
Доброго времени суток, уважаемые читатели. На этот раз мы будем разбираться с тем, как можно оштукатурить стены, чтобы они составили между собой прямой угол. К сожалению, об этом редко кто задумывается, а зря.
Вы спросите: «да зачем это нужно?». А за тем, что мебель и ванны чаще всего сделаны прямоугольными, и если пренебречь несложными расчетами при штукатурке, можно получить нехилые щели между ванной или тумбой и стенами. Оно нам надо? Вот и правильно, поэтому данный урок я призываю вас изучить и отнестись к этой теме серьезно, тем более что сейчас строят просто какое-то г…но, а не дома.
В моей практике был случай, кстати, совсем недавно, когда одна стена комнаты была на пятнадцать сантиметров короче противоположной! Я не знаю, что принимали строители, когда возводили в той квартире межкомнатные перегородки: грибы, ЛСД или еще что, но надеюсь, что их уже вылечили…
Конечно, если у вас дома такие углы, штукатурка тут не поможет, нужно гипсокартонить. Но в большинстве случаев, все же, строители возводят стены в ЛЕГКОЙ степени опьянения, поэтому все еще можно исправить.
Но в большинстве случаев, все же, строители возводят стены в ЛЕГКОЙ степени опьянения, поэтому все еще можно исправить.
Разбор этой темы я предлагаю проводить на примере стандартной по нынешним временам ванной комнаты. Жилье бюджетное, хотя меня всегда пробирает смех, когда это слово применяется для семизначных цифр. Да, всего-то моя зарплата года за три. Итак, имеем вот такую безрадостную картину, как на фото. Батюшки, вместо штукатурки-то у нас – кладочная смесь! Никогда, НИКОГДА не покупайте это, особенно если собираетесь штукатурить самостоятельно! Оно не предназначено для этого, просто заказчику, как всегда, все виднее)) «Берем что подешевле, даже читать надписи на мешках не хотим». Но если хотите гнуть спину дня четыре, а то и пять, постоянно собирать с пола ошметки раствора и стирать их с себя, но сэкономить сорок баксов, то пожалуйста.
Ладно, отвлекся, накипело просто) Дано задание – оштукатурить ванную, разумеется, под маяки, сделав два угла строго прямыми. Без проблем.
Прежде, чем читать дальше, изучите статью Штукатурка стен своими руками, там даны базовые знания об этом процессе: как выставлять маяки, почему лучше пользоваться гипсовой штукатуркой и т.д. В головах многих людей существует мнение, что в ванных нельзя применять гипсовые штукатурки, потому что гипс боится воды. Я считаю эти опасения необоснованными. Наслышан, конечно, о людях, у которых вся плитка отвалилась и тому подобное. Вся проблема здесь стопроцентно заключается в том, что люди эти ничего не грунтовали перед нанесением штукатурки или плиточного клея. Если же грунтовали, то неправильно, либо же наваливали гипсовую штукатурку поверх известковой. Я сам с этим не экспериментировал, но много где пишут о несовместимости этих двух типов штукатурок, так что может быть и такой вариант. Лично я уверен, что, к примеру, Ротбанд годится для оштукатуривания ванных комнат, даже на официальном сайте фирмы-производителя сказано, что он подходит для использования в ванных. Насчет гипсовых смесей подешевле – год назад штукатурил ванную Основитом, заказчик не звонит, значит, все ОК. Так что не верьте тем, кто говорит, что делать такого нельзя. Дело в том, что гипсовые штукатурки – это не чистый гипс, он тут использован лишь как основа. Я проводил тест – брал кусочки высохшей штукатурки разных марок и помещал на сутки в емкость с водой. Им ничего не было! Они не рассыпались и не теряли прочность. Кроме того, какой, по-вашему, процент влаги попадет непосредственно на загрунтованную штукатурку сквозь плитку? Думается мне, что ничтожный.
Так что не верьте тем, кто говорит, что делать такого нельзя. Дело в том, что гипсовые штукатурки – это не чистый гипс, он тут использован лишь как основа. Я проводил тест – брал кусочки высохшей штукатурки разных марок и помещал на сутки в емкость с водой. Им ничего не было! Они не рассыпались и не теряли прочность. Кроме того, какой, по-вашему, процент влаги попадет непосредственно на загрунтованную штукатурку сквозь плитку? Думается мне, что ничтожный.
Опять отвлекся, прошу прощения. Наконец-таки опишу суть технологии оштукатуривания стен под 90 градусов. Она заключается в том, что на первую стену саморезы под маяки мы устанавливаем обычным способом, а на смежные – по угольнику. Вы сейчас, наверняка, представили себе обычный строительный угольничек в 30 см. Нет-нет, нам нужна штука посерьезнее, угольник мы изготовим сами, из правИл. Ведь сама суть его применения сводится к тому, что он должен быть почти от стены до стены. А как же нам изготовить такой угольник и как его проверить? Для этого уже придумана простая и гениальная вещь – египетский треугольник. Это такой треугольник, стороны которого соотносятся между собой как 3:4:5, что означает наличие у него прямого угла автоматически. Так вот, нам всего-то нужно начертить на полу такой треугольник, а потом выровнять по его сторонам два правила и скрепить их друг с другом. Правила нужно соединять прямыми гранями, то есть теми, что без скосов. Таким образом, скос нижнего будет смотреть вниз, а верхнего – вверх.
Теперь поясню все это на примере. Размеры ванной у нас 220×175. Значит, берем два двухметровых правила, одно целое, у второго срезаем порядка 30 см. Подметаем пол на будущем месте разметки. Кстати, ее удобнее всего делать не посреди комнаты, а от стены. Отмечаем на полу у стены начальную точку А и откладываем (опять же по стене) от нее любой размер, кратный трем; в нашем случае удобно взять 120 см. Это будет точка В. Теперь нам нужно изготовить импровизированный циркуль из, например, маркера и шнура, но такого шнура, что бы он не растягивался. Можно использовать и рулетку. От точки А откладываем расстояние, кратное четырем, то есть 160 см, и чертим небольшую дугу. А от точки В откладываем 200 см и тоже чертим дугу. Местом пересечения дуг станет точка С, а линия АС будет перпендикуляром к АВ. Остается уложить наши правила по этим двух линиям и скрепить несколькими саморезами:
Можно использовать и рулетку. От точки А откладываем расстояние, кратное четырем, то есть 160 см, и чертим небольшую дугу. А от точки В откладываем 200 см и тоже чертим дугу. Местом пересечения дуг станет точка С, а линия АС будет перпендикуляром к АВ. Остается уложить наши правила по этим двух линиям и скрепить несколькими саморезами:
Правила взяли самые убогие, не портить же новые. На всякий случай проверяем угол:
Все хорошо, мегаугольник готов к использованию. А пока нам нужно разметить маяки и выставить саморезы на стартовой стене. Мы для этого используем лазер. Сначала отмечаем места для установки маяков. Здесь еще важно сделать так, чтобы все саморезы у пола были в одном уровне, ведь угольник нам придется ставить сразу на четыре из них. Верхние тоже желательно сделать на одном уровне. Их, вообще-то, выставлять будем не по угольнику а просто по вертикальному уровню, прямой угол должен перенестись на них автоматически. Но неплохо было бы его потом проверить.
Выставляем все саморезы опорной стены – формируем базовую плоскость. Следующим шагом нам нужно будет выставить дальние от базовой стены верхний и нижний саморезы. После этого уже пора брать наш титанический угольник. Фактически, нам для достижения угла в 90 градусов необходимо лишь выставить ближний нижний саморез. Предварительно его лучше вкрутить в дюбель по максимуму (учитывая зазор как минимум в 6 мм для маяка). Прикладываем угольник к двум нижним саморезам базы и дальнему на смежной стенке, смотрим, как нам поступать с ближним. Если правило до него не достает – выкручиваем так, что бы доставало. Если правило уперлось в него, но не достает до дальнего самореза – выкручиваем дальний. Может случиться так, что придется несколько раз вкручивать/выкручивать и прикладывать угольник. Ничего страшного, невелик труд. Итак, все, четыре нижних самореза образуют прямой угол.
Верхние выставляем уже по уровню. С лазером я делаю это так: направляю вертикальный луч на шляпку нижнего и смотрю на тень от нее, после чего добиваюсь такой же тени от верхнего самореза.
Такой способ годится, если на одну стену приходится два маяка. Если же их больше, луч будет нужно направлять параллельно стене, то есть он уже не будет падать на шляпки. В этом случае берется отвертка, ею выставляется наименее выпирающий из стены саморез. В месте, где луч будет падать на отвертку ставится отметка, по которой нужно ориентироваться при выставлении остальных саморезов.
Заметьте, у меня отвертка окрашена в красный, и это сделано не просто так. Просто, как ни странно, красный луч гораздо лучше виден на красном фоне, чем на любом другом.
Итак, один прямой угол мы сделали, теперь в точности повторяем те же действия со следующей стеной. Только здесь нужно будет перевернуть угольник, ведь соотношение сторон комнаты поменяется. Выставили нижние саморезы, затем верхние и проконтролировали слой, чтобы везде маяки проходили:
О том, как выставлять маяки, вы уже прочитали в статье «Штукатурка стен». Единственное, я их еще проверяю после установки лазерным уровнем для полной уверенности:
При желании, после того, как маяки схватятся, можно еще раз проверить их угольником. Пока что у меня всегда все совпадало, думаю, и у вас проблем не возникнет. Все, можно приступать непосредственно к штукатурке. У нас в данной ванной получилось вот что:
Если стены готовятся под плитку, то затирать поверхности не нужно, как не нужно и удалять маяки. Также следует помнить, что слой штукатурки под плитку должен быть не менее 1 см.
Вот, в принципе, и все хитрости штукатурки прямых углов. Теперь мы можем смело ставить в них мебель или ванну, никаких щелей точно не будет. Буду польщен, если вы оформите подписку на обновления. В этом случае вы всегда своевременно будете получать анонсы новых статей на почту. Удачи в ремонте своими руками!
Оцените статью:
Поделитесь с друзьями!
Два быстрых способа для разметки прямого угла 90° на местности (теорема Пифагора стоит в стороне) | Строю для себя
Добрый день, уважаемые гости и подписчики моего канала!
Данная статья относится к разметке фундаментов и к построению обноски/выноса осей дома непосредственно перед выемкой грунта.
По сути, соблюдение прямых углов фундамента — это одно из самых важных требований к конструкции, так как от этого напрямую зависит качество работ по сооружению стен и кровли. Отклонение угла на несколько градусов влечет смещение стен относительно фундамента, как представлено на иллюстрации ниже:
Из-за малейшей ошибки, начинаются проблемы с облицовкой цоколя и что немаловажно, ухудшаются эксплуатационные характеристики дома.
Увы, но таких ситуаций море и они берут свое начало из неправильной разметки.
Сегодня, я хотел бы рассказать о двух быстрых способах построения прямых углов на местности без лишних вычислений. Для первого способа нужны две рулетки, для второго — только веревка.
Как вы знаете, построить прямой угол можно:
а) прибегая к вычислениям, т.е. математическим способом. Производя вычисления по теореме Пифагора мы можем отложить полученные значения и получить прямой угол (частный случай — египетский треугольник 3-4-5).
б) геометрическим способом
И, в данной статье я приведу способы геометрического построения без каких-либо вычислений.
Разметка фундамента всегда начинается с привязки одной из его сторон к фасаду или к меже по соседскому забору сбоку. Таким образом, натянув бечевку параллельно забору, у нас уже появляется одна сторона фундамента с которой нам и предстоит работать.
Итак, способ № 1: две рулетки
Отметив угол дома (точка О) на первой стороне дома (прямая АВ), нам нужно отложить две точки, равноудаленные от точки О. После чего, зафиксировать концы двух рулеток на полученных точках и совместить полотна так, чтобы две шкалы пересекались на одном и том же значении.
Прямая, проходящая через точку О и точку пересечения полотен рулеток Х будет перпендикулярна прямой АВ, тем самым мы получили прямой угол между АВ и ОХ, где О — внешний угол фундамента.
Способ №2: веревка
Данный способ похож на первый, только здесь нужна одна веревка. Нам требуется так же отложить от точки О две равноудаленные точки и установить в каждую из них по колышку.
Нам требуется так же отложить от точки О две равноудаленные точки и установить в каждую из них по колышку.
На концах веревки вяжутся петельки (рис.1), которые продеваются в один колышек. Натянув веревку, получаем её центр и отмечаем его (рис.2).
Теперь, накидываем петли на соответствующие колья и натягиваем веревку (рис.3)
Всё. Точка Х, как и в случае с рулетками, образует с точкой О перпендикуляр по отношению к прямой АВ.
Как видите, построение очень простое и что немаловажно — быстрое и точное. Основывается оно на свойстве равнобедренных треугольников, где их высота всегда делит основание на два равных отрезка.
На этом всё! Надеюсь, статья была Вам полезна.
Спасибо за внимание и удачи в строительстве!
Дед рассказал, как 45 лет назад делал «чудо-раствор», что швы даже перфоратор берёт с трудом
«Зачем мудрить?» Проектировщик ландшафта показал, как и куда проще всего отвести воду с крыши (практичное решение)
Всегда догадывался, что на фасовке дурят, но насколько? Взвешиваю 50 кг. цемента и 25 кг. гипса: итоги
Как отмерить прямой угол с помощью рулетки
При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Теорема Пифагора
Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: »В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов» ( a2 + b2 = с2 ), где a и b — катеты, а с — гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.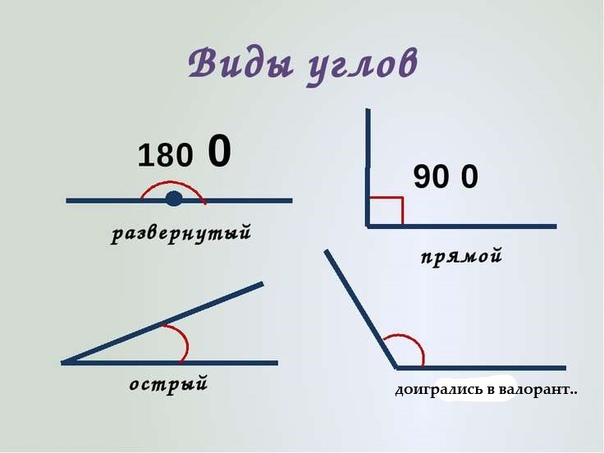
А теперь вернемся к нашим замерам и применим теорему на практике.
Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Египетский треугольник
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник — прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?
a2 + b2 = (32 + 42) = (9 + 16) = 25; √25 = 5.
Как проверить угол с помощью египетского треугольника?
Отмерьте на одной стене отрезок длиной 3 метра, а на другой — отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.
Как отмерить угол, используя рулетку
Можно самостоятельно смастерить угольник для замера углов:
- Соединяем две рейки одна перпендикулярно другой.
- Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
- Прибиваем третью рейку к одной отметке.
- Измеряем гипотенузу, прибиваем рейку ко второй метке.
- Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
- Обрезаем лишние концы.
Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте.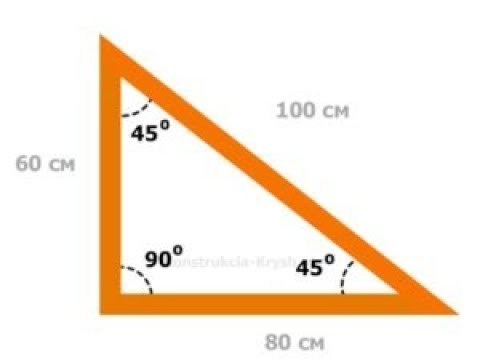 Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.
Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.
Проверяем прямой угол с помощью лазерного уровня
Сегодня вы научитесь с помощью лазерного уровня проверять соответствие угла 90°. Для этого вам всего лишь нужно следовать пошаговой инструкции, подготовленной специалистом нашей компании.
Пошаговая инструкция:
Шаг первый. Выставьте лазерный нивелир вдоль первой стены, для этого:
1. От одного края проверяемой стены отмерьте 10 см с помощью рулетки. Поставьте карандашом на полу или стене отметку. Если отделка чистовая, используйте малярный скотч как поверхность для отметки (наклейте его на пол или на стену и разметьте по нему).
2. С помощью рулетки отложите от другого края проверяемой стены 10 см. Поставьте отметку карандашом на полу или на стене.
3. Поставьте лазерный нивелир в углу примыкания двух проверяемых стен, на расстоянии 30-35 см от второй проверяемой стены.
4. Включите отображение вертикальных плоскостей.
5. Нацельте вертикальную плоскость на ближайшую отметку.
6. Путем передвижения построителя плоскостей к или от первой проверяемой стены, выставьте лазерный уровень так, чтобы его вертикальная плоскость проходила через обе поставленные отметки.
Шаг второй. На лазерном уровне включите отображение перпендикулярной вертикальной плоскости.
Шаг третий. Вдоль поверхности проверяемой стены с помощью рулетки замерьте расстояние от первой проверяемой стены до первой построенной плоскости.
Шаг четвертый. Теперь сверьте это расстояние с изначальным (10 см). Если расстояние больше 10 см, значит на этом месте яма. Если расстояние меньше 10 см, значит на этом месте бугор.
Шаг пятый. Затем с помощью рулетки замерьте расстояние от первой проверяемой стены до первой построенной плоскости по высоте первой проверяемой стены
Шаг шестой. И сверьте это расстояние с изначальным (10 см). Если расстояние больше 10 см, значит проверяемая стена завалена от вас. Если расстояние меньше 10 см, значит проверяемая стена завалена на вас.
И сверьте это расстояние с изначальным (10 см). Если расстояние больше 10 см, значит проверяемая стена завалена от вас. Если расстояние меньше 10 см, значит проверяемая стена завалена на вас.
Шаг седьмой. Повторяем пункты 3,4,5,6 этой инструкции в отношении второй проверяемой стены.
Запомните: Если расстояния между краями первой и краями второй стен попарно одинаково расположены от заданных плоскостей, то угол между этими двумя примыкающими стенами соответствует 90 градусов.
Если хоть одна из стен дальним краем направлена от вас, угол тупой.
Если хоть одна из стен дальним краем направлена к вам, угол между стенами острый.
Посмотрите наше портфолио и убедитесь в этом лично
Также вы можете посмотреть, как проверить прямой угол с помощью лазерного уровня в формате видео. Это займет у вас чуть больше 1 минуты. Не забудьте поставить лайк, если ролик окажется для вас полезным.
cccp3d.ru | Угол 90 градусов на отливаемой детали
By
tompsongun · Posted
@none , вот про квадратик — не могу даже предположить. в этом месте, я повторил как в МПроп — вернее скопировал оттуда. еслиб квадратик был перед второй строкой — мне это ожидаемо бы показалось ))
попробуйте добавить в редакторе макросов такое: & Chr$(13) перед & Chr$(10) — на следующей картинке красным выделил
и ещё вариант — после есть пробел — удалить его — на картинке синеньким:
или вот запаковал три варианта (надо только поочередно попереименовывать файлы — стереть лишнее в конце имени:SaveAsCopyReplace_вариации по удалению квадратика.zip, если что-то поможет, подскажите — внесу общую правку.
про удаление файлов в корзину — сразу хотел такое — но там для vba прям сложная обработка с обращением к системным путям еще чего-то. может когда поднаторею имли повезёт )) удастся реализовать — там кода строк, наверно на 50-70 — что находил в инете.
с наименованием_ФБ, так же, если осилю хотелось бы сделать разбиение не на 2 сроки как сечас, но и на 3-4 с автоматическим изменением шрифта, для этого, видимо надо сделать цикл со сравнением количества символов входящих в строку.
а проще, скорее всего как-то поправить шаблоны чертежей — чтобы было что-то вписано в эту заметку основной надписи и «подёрганы» границы этой заметки — солид вроде запоминает в дальнейшем это. надо пробовать ))
и что-то придумать для обработки такой, например, записи: 12345_футорка 1_2-1_8.
преобразовать его в обозначение 12345, разделитель _ , а последующие _ превращать в слеш: футорка 1/2-1/8.
себе-то я сделаю — у нас разделитель «пробел», а тут заковыка )
но всё это, увы, не скоро. если кто сам захочет доработать и выложить — я абсолютно не против, только дополняйте формы «эволюция» и «справка». чтобы преемственность оставалась. если что будут «форки» )).
——————————————————-
@DuS , вот у себя нашёл от создателя partTreeRename )) : NotAsToolbox(1.0.0).zip
до конца не пробовал )) — не преобразовывал. ругается на ключ документ-манагер, в папке есть текстовичок соотв., но он пуст был и есть.
Виды углов: острый, прямой, тупой, развёрнутый, выпуклый и полный
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом.
 Прямой угол обычно обозначается не дугой, а уголком:
Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.
Острый, тупой, прямой и правый
Угол измеряет величину поворота
Названия углов
По мере увеличения угла название меняется:
Попробуйте сами:
В одной схемеЭта диаграмма может помочь вам запомнить: Также: Acute, Obtuse и Reflex расположены в алфавитном порядке. |
Также: буква «А» имеет острый угол.
Будьте осторожны при измерении
| Меньший угол — тупой угол , , но больший угол — угол отражения |
Поэтому при именовании углов убедитесь, что
что вы знаете , какой угол
просил !
Положительные и отрицательные углы
При измерении от линии:
- положительный угол идет против часовой стрелки (направление, противоположное движению часов)
- отрицательный угол идет по часовой стрелке
Пример: −67 °
Части угла
Угловая точка угла называется вершиной
И две прямые стороны называются руками
Угол равен повороту между каждым плечом.
Как маркировать углы
Есть два основных способа маркировать углы:
1. Назовите угол, обычно строчной буквой, например a или b , или иногда греческой буквой, например α (альфа) или θ (тета)
2. или тремя буквами на фигуре, которые определяют угол, при этом средняя буква указывает на то, где на самом деле находится угол (его вершина).
Пример угла « a » — « BAC », а угол « θ » — « BCD »
Что такое прямой угол? — [Определение, факты и примеры]
Right Angle Games
Right Angle
Определение прямых углов в различных двухмерных формах. Помните, вы можете распознать прямые углы, глядя на перпендикулярные линии.
Помните, вы можете распознать прямые углы, глядя на перпендикулярные линии.
охватывает Common Core Curriculum 4.G.2Играть сейчасПосмотреть все игры по геометрии >>
Учитесь с помощью полной программы обучения математике K-5
Что такое прямой угол?
В геометрии, когда два луча встречаются в общей точке, они образуют угол. Точка встречи двух лучей называется вершиной.
Углы измеряются в градусах (символ: ˚)
Некоторые общие типы углов — острые, прямые и тупые углы.
Прямой угол
Когда две прямые пересекаются друг с другом под углом 90 ° или перпендикулярны друг другу на пересечении, они образуют прямой угол. Прямой угол обозначается символом ∟.
На данном изображении показаны различные образования прямого угла.
Мы можем найти прямые углы в формах.
Квадрат или прямоугольник имеет четыре угла с прямыми углами.
Примеры прямых углов повсюду вокруг нас.Мы можем видеть прямые углы в углах комнаты, книги, куба, окон и в некоторых других местах.
Вертикальная и горизонтальная линии обычно образуют прямые углы. Однако пересекающиеся друг с другом диагональные линии тоже образуют прямые углы. Если вы нарисуете диагонали квадрата, ромба или воздушного змея, угол пересечения составит 90 градусов и, следовательно, будет прямым углом.
Пример ромба и воздушного змея с диагоналями, пересекающимися под прямым углом.
Как нарисовать прямой угол с помощью транспортира?
1 . Начните с рисования горизонтальной линии.
2 . Теперь поместите транспортир на горизонтальную линию.
3 . Измерьте 90˚ и отметьте его точкой.
4 . Теперь с помощью шкалы нарисуйте прямую линию от этой точки до горизонтальной линии.
Интересные факты
|
Типы углов — объяснение и примеры
В природе существуют разные типы углов , , и каждый из них имеет большое значение в нашей повседневной жизни.
Например, , архитекторы и инженеры используют углы при проектировании машин, зданий, дорог и мостов.
В спорте спортсмены используют углы для улучшения своих результатов. Например, человек должен вращаться с диском под определенным углом, чтобы бросить его на короткое расстояние. В футболе вы должны использовать определенный угол, чтобы передать мяч следующему игроку.
Плотники и ремесленники также используют углы для изготовления таких предметов, как диваны, столы, стулья, ведра и т. Д. Художники используют углы для набросков портретов и картин. Модельеры также используют углы, чтобы подобрать лучшие наряды. По этим причинам необходимо изучить различные типы углов.
(Основное объяснение углов можно найти в предыдущей статье «Углы».)
Различные типы углов
Углы классифицируются на основе:
Классификация углов по их величине
Там семь типов углов, основанных на их градусном измерении. К ним относятся:
- нулевые углы
- острые углы
- прямые углы
- тупые углы
- прямые углы
- углы отражения
- полный угол
нулевой угол
нулевой угол (0 °) угол образуется, когда оба плеча угла находятся в одном и том же положении.
Иллюстрация:
∠ RPQ = 0 ° (нулевой угол)
Острый угол
Острый угол — это угол, который больше 0 °, но меньше 90 °. Общие примеры острых углов включают: 15 °, 30 °, 45 °, 60 ° и т. Д.
Общие примеры острых углов включают: 15 °, 30 °, 45 °, 60 ° и т. Д.
∠ XYZ больше 0 °, но меньше 90 ° (острый угол)
Угол 90 градусов
Угол в 90 градусов, также известный как прямой угол, — это угол, размер которого равен 90 °, и называется прямым углом.Прямые углы изображаются в виде небольшой квадратной рамки между плечами угла.
Иллюстрация:
∠ ABC = 90 ° (прямой угол)
В следующем разделе (Треугольники) будет целая статья о прямоугольных треугольниках.
Тупой угол
Тупой угол — это тип угла, градусы которого больше 90 °, но меньше 180 °. Примеры тупых углов: 100 °, 120 °, 140 °, 160 °, 170 ° и т. Д.
∠ PQR — тупой угол, потому что он меньше 180 ° и больше 90 °.
Прямой угол
Как следует из названия, прямой угол — это угол, размер которого равен 180 ° (прямая линия)
Иллюстрация:
∠ XYZ = 180 ° (прямой угол)
Угол отражения
Углы отражения — это углы, градусы которых больше 180 °, но меньше 360 °. Общие примеры углов рефлекса: 200 °, 220 °, 250 °, 300 °, 350 ° и т. Д.
Иллюстрация:
∠ PQR больше 180 °, но меньше 360 °
Полный угол
Полный угол равен до 360 °.1 оборот равен 360 °.
Иллюстрация:
Классификация углов на основе поворота
В зависимости от направления вращения углы можно разделить на две категории, а именно;
- Положительные углы
- Отрицательные углы
Положительные углы
Положительные углы — это типы углов, измерения которых проводятся против часовой стрелки от основания.
Отрицательные углы
Отрицательные углы измеряются по часовой стрелке от основания.
Другие типы углов
Помимо рассмотренных выше углов, существуют другие типы углов, известные как парные углы. Их называют парными углами, потому что они появляются парами, чтобы показать определенное свойство. Это:
Их называют парными углами, потому что они появляются парами, чтобы показать определенное свойство. Это:
- Соседние углы имеют одинаковую вершину и плечо.
- Дополнительные углы: парные углы, которые в сумме составляют 90 °.
- Дополнительные углы: парные углы, сумма углов которых равна 180º.
- Вертикально противоположные углы.Вертикально противоположные углы равны.
- Альтернативные внутренние углы: Альтернативные внутренние углы — это парные углы, образующиеся, когда линия пересекает две параллельные линии. Чередующиеся внутренние углы всегда равны друг другу.
- Альтернативные внешние углы : Альтернативные внешние углы — это просто вертикальные углы альтернативных внутренних углов. Альтернативные внешние углы эквивалентны.
- Соответствующие углы : Соответствующие углы — это парные углы, образующиеся, когда прямая пересекает пару параллельных прямых.Соответствующие углы также равны друг другу.
Мы видели краткий обзор различных типов углов. Далее мы увидим подробные статьи о наиболее распространенных типах углов (Дополнительные углы, Дополнительные углы и т. Д.).
Предыдущий урок | Главная страница | Следующий урок
Как найти угол в прямоугольном треугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
как
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Отношения и размеры — Факты о прямоугольном треугольнике
Вы уже
встретили прямоугольный треугольник на предыдущем уроке. Подружитесь с ним! Он
один из самых популярных существующих полигонов, в основном из-за его решения проблем
способности.
Прямоугольный треугольник
имеет один угол, равный 90 градусам. Прямоугольный треугольник тоже может быть равнобедренным.
треугольник — это означает, что у него две стороны, которые равны. Правый равнобедренный
треугольник имеет угол 90 градусов и два угла 45 градусов. Это единственный
прямоугольный треугольник, который является равнобедренным треугольником. Эта версия прямоугольного треугольника
настолько популярны, что их пластиковые модели изготавливают и используют архитекторы,
инженеры, плотники и художники-графики в их дизайне и строительстве
Работа.
Еще одно интересное
Прямой треугольник — это треугольник 30-60-90 градусов. Отношение этого треугольника
самая длинная сторона к самой короткой стороне — «два к одному». То есть самая длинная сторона
вдвое длиннее самой короткой стороны. Он тоже изготовлен из пластика и
широко используется в приложениях для проектирования, рисования и строительства.
Вы можете найти
бесконечное количество примеров прямоугольных треугольников. Один из самых известных —
треугольник «3, 4, 5.«
Египтяне
использовал этот треугольник для топографической съемки. Некоторые считают, что они тоже его использовали
чтобы помочь спроектировать их пирамиды. Независимо от того, сделали они это или нет, треугольник 3-4-5
до сих пор используется геодезистами. Плотники и плотники также используют его для изготовления
Плотники и плотники также используют его для изготовления
их углы квадратные.
Пифагор был
греческий математик, живший около 2500 лет назад и разработавший
самая известная формула в геометрии, возможно, во всей математике! Он доказал
что для прямоугольного треугольника сумма квадратов двух сторон, соединяющих
под прямым углом равняется квадрату третьей стороны.Третья сторона —
сторона, противоположная прямому углу — называется гипотенузой прямоугольного треугольника.
Две более короткие стороны обычно называют «ногами».
Эта формула
называется теоремой Пифагора в честь Пифагора. Обычно пишут
как показано в приведенном ниже уравнении, где a и b — это меры
катеты треугольника c — мера гипотенузы.
Давай
попробуйте теорему Пифагора, используя этот прямоугольный треугольник со сторонами 5
и 12 см, а гипотенуза 13 см.Мы можем проверить, что теорема Пифагора
верно путем подстановки значений. Квадратный корень из 169 равен 13, что
— мера гипотенузы в этом треугольнике.
The
Теорема Пифагора имеет множество применений. Вы можете использовать его, чтобы проверить, действительно ли
треугольник — это прямоугольный треугольник. Или вы можете использовать его, чтобы найти недостающие меры
сторон. Воспользуемся теоремой Пифагора, чтобы найти недостающую меру
катет прямоугольного треугольника SAM.
Заменить
значения в формулу и выполните вычисления, как это. Мы находим, что
квадрат гипотенузы или c в квадрате равен 400. Чтобы найти c, мы
извлекаем квадратный корень из 400, то есть 20. Это значение, которое мы ищем.
для, недостающий размер ноги,
Калькулятор прямоугольного треугольника
Укажите 2 значения ниже, чтобы рассчитать другие значения прямоугольного треугольника. Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 3, пи / 4 и т. Д.
Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 3, пи / 4 и т. Д.
Калькулятор связанного треугольника | Калькулятор теоремы Пифагора
Прямой треугольник
Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °. Правые треугольники и отношения между их сторонами и углами являются основой тригонометрии.
В прямоугольном треугольнике сторона, противоположная углу 90 °, является самой длинной стороной треугольника и называется гипотенузой. Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон.Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже. . В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая представляет собой длину от вершины прямого угла треугольника до гипотенузы треугольника. Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
Если все три стороны прямоугольного треугольника имеют целые числа, он называется треугольником Пифагора. В треугольнике этого типа длины трех сторон в совокупности известны как тройка Пифагора. Примеры включают: 3, 4, 5; 5, 12, 13; 8, 15, 17 и т. Д.
Площадь и периметр прямоугольного треугольника рассчитываются так же, как и любого другого треугольника. Периметр представляет собой сумму трех сторон треугольника, а площадь можно определить с помощью следующего уравнения:
Специальные прямоугольные треугольники
треугольник 30 ° -60 ° -90 °:
30 ° -60 ° -90 ° относится к угловым измерениям в градусах этого типа специального прямоугольного треугольника. В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием указанного выше соотношения. Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сб .:
В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием указанного выше соотношения. Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сб .:
Углы: 30 °: 60 °: 90 °
Соотношение сторон: 1: √3: 2
Длина сторон: a: 5: c
Тогда используя известные отношения сторон этого особого типа треугольника:
Как видно из вышеизложенного, знание только одной стороны треугольника 30 ° -60 ° -90 ° позволяет относительно легко определить длину любой из других сторон.Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6.
45 ° -45 ° -90 ° треугольник:
Треугольник 45 ° -45 ° -90 °, также называемый равнобедренным прямоугольным треугольником, поскольку он имеет две стороны равной длины, представляет собой прямоугольный треугольник, в котором стороны, соответствующие углам, составляют 45 ° -45 ° -90 °, соблюдайте соотношение 1: 1: √2. Подобно треугольнику 30 ° -60 ° -90 °, знание длины одной стороны позволяет определить длины других сторон треугольника 45 ° -45 ° -90 °.
Углы: 45 °: 45 °: 90 °
Соотношение сторон: 1: 1: √2
Длина сторон: a: a: c
Учитывая c = 5:
Треугольники 45 ° -45 ° -90 ° можно использовать для вычисления тригонометрических функций, кратных π / 4.
Как построить угол 90 градусов с помощью циркуля и линейки или линейки
На этой странице мы покажем, как построить (нарисовать) угол в 90 градусов с помощью циркуля и линейки или линейки. Есть разные способы сделать это, но в этой конструкции мы используем свойство
Теорема Фалеса.Создаем круг, в котором
вершина
искомого прямого угла — это точка на окружности. Теорема Фалеса гласит, что любой
Теорема Фалеса гласит, что любой
диаметр круга
подает
под прямым углом к любой точке окружности.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как
распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов
или когда компьютер недоступен.
Объяснение метода
Фактически это та же конструкция, что и при построении перпендикуляра в конечной точке луча.Другой способ сделать это —
Проба
Эта конструкция работает с использованием теоремы Фалеса. Он создает круг, в котором вершина нужного прямого угла является точкой на окружности.
| Аргумент | Причина | |
|---|---|---|
| 1 | Отрезок AB равен диаметру центра окружности D | AB — прямая линия, проходящая через центр. |
| 2 | Угол ACB имеет размер 90 °. | Диаметр круга всегда образует угол 90 ° с любой точкой (C) на окружности. См. Теорему Фалеса. |
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист, содержащий две проблемы, которые можно попробовать.
Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.
Другие конструкции, страницы на сайте
Строки
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
.

 Прямой угол обычно обозначается не дугой, а уголком:
Прямой угол обычно обозначается не дугой, а уголком: